Leonhard Euler
Leonhard Paul Euler (pron. ˈɔʏlɐ n'alemán) (15 d'abril de 1707, Basilea – 18 de setiembre de 1783, San Petersburgu), conocíu como Leonhard Euler, foi un matemáticu y físicu suizu. Trátase del principal matemáticu del sieglu XVIII y unu de los más grandes y prolíficos de tolos tiempos.
Vivió en Rusia y Alemaña la mayor parte de la so vida y realizó importantes descubrimientos n'árees tan diverses como'l cálculu o la teoría de grafos. Tamién introdució gran parte de la moderna terminoloxía y notación matemática, particularmente pa l'área del analís matemáticu, como por casu la noción de función matemática.[14] Coles mesmes conózse-y polos sos trabayos nos campos de la mecánica, óptica y astronomía.
Euler foi unu de los matemáticos más prolíficos, y calcúlase que les sos obres completes aconceyaes podríen ocupar ente 60 y 80 volúmenes.[15] Una afirmación atribuyida a Pierre Simon Laplace espresa la influencia d'Euler nos matemáticos posteriores: «Lean a Euler, lean a Euler, él ye'l maestru de toos nós.»[16]
En conmemoración so, Euler apaeció na serie sesta de los billetes de 10 francos suizos, según en numberosos sellos postales tanto suizos como alemanes y rusos. El asteroide (2002) Euler recibió esi nome nel so honor.
Biografía[editar | editar la fonte]
Primeros años[editar | editar la fonte]

Euler nació en Basilea (Suiza), fíu de Paul Euler, un pastor calvinista, y de Marguerite Brucker, fía d'otru pregueru. Tuvo dos hermanes pequeñes llamaes Anna Maria y Maria Madalena. Poco dempués de la so nacencia, la so familia treslladóse de Basilea al cercanu pueblu de Riehen, onde Euler pasó la so infancia. Pela so parte, Paul Euler yera amigu de los Bernoulli, famosa familia de matemáticos ente los que destacaba Johann Bernoulli, que nesi momentu yera yá consideráu'l principal matemáticu européu, y qu'exerciera una gran influyencia sobre'l mozu Leonhard.
La educación formal d'Euler empezó na ciudá de Basilea, onde lu unviaron a vivir cola so güela materna. A la edá de 13 años matricular na Universidá de Basilea y en 1723 recibió'l títulu de maestru de Filosofía tres una disertación comparativa de les filosofíes de René Descartes y Isaac Newton. Daquella, Euler tomaba lleiciones particulares con Johann Bernoulli tolos sábados pela tarde, quien afayó rápido l'increíble talentu del so nuevu pupilu pa les matemátiques.[17]
Naquella dómina Euler dedicar a estudiar teoloxía, griegu y hebréu, siguiendo los deseos del so padre, y cola vista puesta en aportar a tamién pregueru. Johann Bernoulli intervieno pa convencer a Paul Euler de que Leonhard taba destináu a ser un gran matemáticu. En 1726 Euler remató'l so Doctoráu con una tesis sobre la espardimientu del soníu sol títulu De Sono[18] y en 1727 participó nel concursu promovíu pola Academia de les Ciencies francesa pol cual solicitábase a los concursantes qu'atoparen la meyor forma posible d'allugar el mástil nun buque. Ganó'l segundu puestu, detrás de Pierre Bouguer, que ye conocíu por ser el padre de l'arquiteutura naval. Más palantre Euler consiguiría ganar esi premiu hasta en dolce causes.[19]
San Petersburgu[editar | editar la fonte]
Por aquella dómina, los dos fíos de Johann Bernoulli, Daniel y Nicolás, atopábense trabayando na Academia de les ciencies de Rusia en San Petersburgu. En xunetu de 1726, Nicolás morrió d'apendicitis en viviendo un añu en Rusia y, cuando Daniel asumió'l cargu del so hermanu nel departamentu de matemátiques y física, encamentó que'l yá que había dexáu vacante en fisioloxía fora ocupáu pol so amigu Euler. En payares d'esi mesmu añu Euler aceptó la ufierta, anque retrasó la so salida escontra San Petersburgu mientres intentaba consiguir, ensin ésitu, un puestu de profesor de física na Universidá de Basilea.[20]

Euler llegó a la capital rusa'l 17 de mayu de 1727. Foi xubíu dende'l so puestu nel departamentu médicu de l'Academia a otru nel departamentu de matemátiques, nel que trabayó con Daniel Bernoulli, de cutiu n'estrecha collaboración. Euler aprendió'l rusu y establecióse finalmente en San Petersburgu a vivir. Llegó inclusive a tomar un trabayu adicional como médicu de l'Armada de Rusia.[21]
L'Academia de San Petersburgu, creada por Pedru I de Rusia, tenía l'oxetivu d'ameyorar el nivel educativu en Rusia y d'amenorgar la diferencia científica esistente ente esi país y l'Europa Occidental. Como resultancia, implementáronse una serie de midíes p'atraer a eruditos estranxeros como Euler. L'Academia tenía amplios recursos financieros y una biblioteca bien estensa, estrayida direutamente de les biblioteques privaes de Pedru I y de la nobleza. L'Academia almitía a un númberu bien amenorgáu d'estudiantes pa facilitar el llabor d'enseñanza, al empar que se enfatizaba el llabor d'investigación y ufiertábase a la facultá tanto'l tiempu como la llibertá pa resolver cuestiones científiques.[22]
Sicasí, la principal benefactora de l'Academia, la emperatriz Catalina I de Rusia, que siguiera coles polítiques progresistes del so home, morrió'l mesmu día de la llegada d'Euler a Rusia. La so muerte amontó'l poder de la nobleza, yá que el nuevu emperador pasó a ser Pedru II de Rusia, daquella un neñu de tan solo 12 años d'edá. La nobleza abarruntaba de los científicos estranxeros de l'Academia, polo que cortó la cuantía de recursos dedicaos a la mesma y provocó otra serie de dificultaes pa Euler y los sos colegues.
Les condiciones ameyoraron llixeramente tres la muerte de Pedru II, y Euler foi adulces xubiendo na xerarquía de l'Academia, convirtiéndose en profesor de física en 1731. Dos años más tarde, Daniel Bernoulli, fartu de les dificultaes que-y plantegaben la censura y l'hostilidá a la que s'enfrentaben en San Petersburgu, dexó la ciudá y volvió a Basilea. Euler asocedió-y como direutor del departamentu de matemátiques.[23]
El 7 de xineru de 1734, Euler casóse con Katharina Gsell, fía d'un pintor de l'Academia. La moza pareya mercó una casa al llau del ríu Nieva y llegó a concebir trece fíos, magar namái cinco sobrevivieron hasta la edá adulta.[24] El mayor d'estos fíos, Johann Euler, foi matemáticu y astrónomu y miembru l'Academia de Berlín dende 1754.
Berlín[editar | editar la fonte]
Esmolecíu polos acontecimientos políticos que taben teniendo llugar en Rusia, Euler partió de San Petersburgu el 19 de xunu de 1741 p'aceptar un cargu na Academia de Berlín, cargu que-y fuera ufiertáu por Federicu II el Grande, rei de Prusia. Vivió venticinco años en Berlín, onde escribió más de 380 artículos. Tamién publicó equí dos de les sos principales obres: la Introductio in analysin infinitorum, un testu sobre les funciones matemátiques publicáu en 1748, y la Institutiones calculi differentialis,[25] publicada en 1755 y que trataba sobre'l cálculu diferencial.[26]
Amás, ufiertóse-y a Euler un puestu como tutor de la princesa d'Anhalt-Dessau, la sobrina de Federicu. Euler escribió más de 200 cartes empobinaes a la princesa que más tarde seríen arrexuntaes nun volume titulao Cartes d'Euler sobre distintos temes de Filosofía Natural dirixíes a una Princesa alemana. Esti trabayu arrexuntaba la esposición d'Euler sobre varios temes de física y matemátiques, según una visión de la so personalidá y de les sos creencies relixoses. El llibru convertir nel más lleíu de toles sos obres, siendo publicáu a lo llargo y anchu del continente européu y nos Estaos Xuníos. La popularidá que llegaron a algamar estes Cartes sirve de testimoniu sobre l'habilidá d'Euler de comunicar cuestiones científiques a una audiencia menos cualificada.[26]
A pesar de la inmensa contribución d'Euler al prestíu de l'Academia, foi obligáu finalmente a dexar Berlín. El motivu d'esto foi, en parte, un conflictu de personalidá ente'l matemáticu y el mesmu rey Federicu, que llegó a ver a Euler como una persona bien pocu sofisticada, y especialmente en comparanza col círculu de filósofos que'l rei alemán llograra rexuntar na Academia. Voltairesobremanera, yera unu d'esos filósofos y gociaba d'una posición preeminente nel círculu social del rei. Euler, como un simple home de calter relixosu y trabayador, yera bien convencional nes sos creencies y nos sos gustos, representando en cierta forma lo contrario que Voltaire. Euler tenía conocencies llindaes de retórica y solía aldericar cuestiones sobre les que tenía poques conocencies, lo cual faía-y un oxetivu frecuente de los ataques del filósofu.[26] Por casu, Euler protagonizó dellos discutinios metafísicos con Voltaire, de les que solía retirase enfurecido pola so incapacidá na retórica y la metafísica. Federicu tamién amosó'l so descontentu coles habilidaes práutiques d'inxeniería d'Euler:
Quería tener una bomba d'agua nel mio xardín: Euler calculó la fuercia necesario de les ruedes p'alzar l'agua a un depósitu, dende'l que cayería dempués al traviés de canalizaciones pa finalmente esquitar nel palaciu de Sanssouci. El mio molín foi construyíu de forma xeométrica y nun podía alzar una bocanada d'agua hasta más allá de cinco pasos escontra la reserva. ¡Vanidá de les vanidaes! ¡Vanidá de la xeometría!
Deterioru de la visión[editar | editar la fonte]

La vista d'Euler foi empiorando a lo llargo de la so vida. Nel añu 1735 Euler sufrió una fiebre casi fatal, y tres años dempués de dichu acontecimientu quedó casi ciegu del so güeyu derechu. Euler, sicasí, prefería acusar d'esti fechu al trabayu de cartografía que realizaba pa l'Academia de San Petersburgu.
La vista d'esi güeyu empioró a lo llargo de la so estancia n'Alemaña, hasta'l puntu de que Federicu faía referencia a él como'l Cíclope. Euler más tarde sufrió tabayóns nel so güeyu sanu, l'esquierdu, lo que-y dexó práuticamente ciegu poques selmanes dempués de ser diagnosticaes. A pesar d'ello, paez que los sos problemes de visión nun afectaron a la so productividá intelectual, yá que lo compensó cola so gran capacidá de cálculu mental y el so memoria fotográfica. Por casu, Euler yera capaz de repitir la Eneida de Virxiliu dende l'empiezu hasta'l final y ensin duldar en nengún momentu, y en cada páxina de la edición yera capaz d'indicar qué llinia yera la primera y cuál yera la postrera.[15] Tamién se sabía de memoria les fórmules de trigonometría y les primeres 6 potencies de los primeres 100 númberos primos.[29]
Pasó los últimos años de la so vida ciegu, pero siguió trabayando. Munchos trabayos dictar al so fíu mayor. Esto amontó'l respetu que la comunidá científica yá tenía por él. El matemáticu francés François Arago (1786–1853) refirióse allá una vegada a él diciendo: "Euler calculaba ensin esfuerciu aparente, como los homes alienden, o como les águiles sostener nel aire".[ensin referencies]
Torna a Rusia[editar | editar la fonte]

La situación en Rusia ameyorara descomanadamente tres l'ascensu de Catalina la Grande, polo qu'en 1766 Euler aceptó una invitación pa volver a l'Academia de San Petersburgu y pasar ellí'l restu de la so vida. La so segunda dómina en Rusia, sicasí, tuvo marcada pola traxedia: una quema en San Petersburgu en 1771 costó-y el so casa y casi la so vida, y en 1773 perdió a la so esposa, dempués de 40 años de matrimoniu. Euler volvió casase tres años más tarde.
El 18 de setiembre de 1783, Euler finó na ciudá de San Petersburgu en sufriendo un accidente cerebrovascular y foi soterráu xunto cola so esposa nel Campusantu Luteranu allugáu na isla de Vasilievsky. Los sos restos fueron treslladaos polos soviéticos al Monesteriu d'Alejandro Nevski (tamién conocíu como Leningradsky Nikropol).
El matemáticu y filósofu francés Nicolas de Condorcet escribió'l so aponderamientu funeral pa l'Academia francesa.
…il cessa de calculer et de vivre — … dexó de calcular y de vivir.[30]
Pela so parte, Nikolaus von Fuss, afiáu d'Euler y secretariu de l'Academia Imperial de San Petersburgu, escribió un rellatu de la so vida xunto con un llistáu de les sos obres.
Contribución a les matemátiques y a otres árees científiques[editar | editar la fonte]
Euler trabayó práuticamente en tolos ámbitos de les matemátiques: xeometría, cálculu, trigonometría, álxebra, teoría de númberos, amás de física continua, teoría llunar y otres árees de la física. Adicionalmente, apurrió de manera relevante a la lóxica matemática cola so diagrama de conxuntos.
Foi unu de los matemáticos más prolíficos de la hestoria. La so actividá de publicación foi incesante (un permediu de 800 páxines d'artículos al añu na so dómina de mayor producción, ente 1727 y 1783), y una bona parte de la so obra completa ta ensin publicar. El llabor d'escoyeta y publicación completa de los sos trabayos, llamaos Opera Omnia,[31] empezó en 1911 y hasta la fecha llegó a publicar 76 volúmenes. El proyeutu inicial entamaba'l trabayu sobre 887 títulos en 72 volúmenes. Considérase-y el ser humanu con mayor númberu de trabayos y artículos en cualquier campu del saber, namái equiparable a Gauss. Si imprimiérense tolos sos trabayos, munchos de los cualos son d'una importancia fundamental, ocuparíen ente 60 y 80 volúmenes.[15] Amás, y según el matemáticu Hanspeter Kraft, presidente de la Comisión Euler de la Universidá de Basilea, nun s'estudió más d'un 10 % de los sos escritos.[32] Por tou ello, el nome d'Euler ta acomuñáu a un gran númberu de cuestiones matemátiques.
Créese que foi'l que dio orixe al pasatiempos Sudoku creando una serie de pautes pal cálculu de probabilidaes.[33]
Notación matemática[editar | editar la fonte]
Euler introdució y popularizó delles convenciones referentes a la notación nos escritos matemáticos nos sos numberosos y bien utilizaos llibros de testu. Posiblemente lo más notable foi la introducción del conceutu de función matemática,[14] siendo'l primeru n'escribir f(x) pa faer referencia a la función f aplicada sobre l'argumentu x. Esta nueva forma de notación ufiertaba más comodidá frente a los rudimentarios métodos del cálculu infinitesimal esistentes hasta la fecha, empecipiaos por Newton y Leibniz, pero desenvueltos basándose nes matemátiques del postreru.
Tamién introdució la notación moderna de les funciones trigonométriques, la lletra y como base del llogaritmu natural o neperianu (el númberu e ye conocíu tamién como'l númberu d'Euler), la lletra griega Σ como símbolu de los sumatorios y la lletra pa faer referencia a la unidá imaxinaria.[34] L'usu de la lletra griega π pa faer referencia al cociente ente'l llargor de la circunferencia y el llargor del so diámetru tamién foi popularizáu por Euler, anque él nun foi'l primeru n'usar esi símbolu.[35]
Analís[editar | editar la fonte]
El desenvolvimientu del cálculu yera una de les cuestiones principales de la investigación matemática del sieglu XVIII, y la familia Bernoulli fuera responsable de gran parte del progresu realizáu hasta entós. Gracies a la so influencia, l'estudiu del cálculu convertir n'unu de los principales oxetos del trabayu d'Euler. Magar dalgunes de les sos demostraciones matemátiques nun son aceptables so los estándares modernos de rigor matemático,[36] ye ciertu que les sos idees supunxeron grandes meyores nesi campu.
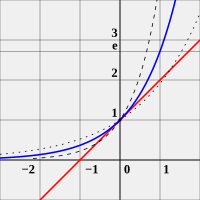
El númberu e[editar | editar la fonte]
Euler definió la constante matemática conocida como númberu como aquel númberu real tal que'l valor de la derivada (la rimada de la llinia tanxente) de la función x nel puntu ye esautamente 1. Ye más, ye'l númberu real tal que la función x tiense como derivada a sigo mesma. La función x ye tamién llamada función esponencial y la so función inversa ye'l llogaritmu neperianu, tamién llamáu llogaritmu natural o llogaritmu en base .
El númberu puede ser representáu como un númberu real en delles formes: como una serie infinita, un productu infinitu, una fracción continua o como la llende d'una socesión. La principal d'estes representaciones, particularmente nos cursos básicos de cálculu, ye como la llende:
y tamién como la serie:
Amás, Euler ye bien conocíu pol so analís y el so frecuente usu de la serie de potencies, esto ye, la espresión de funciones como una suma infinita de términos como la siguiente:
Unu de los famosos llogros d'Euler foi'l descubrimientu de la espansión de series de potencies de la función arcotangente. El so atrevíu, anque, según los estándares modernos, téunicamente incorreutu usu de les series de potencies dexáron-y resolver el famosu problema de Basilea en 1735,[36] pol cual quedaba demostráu que:

Euler introdució l'usu de la función esponencial y de los llogaritmos nes demostraciones analítiques. Afayó formes pa espresar delles funciones logarítmiques utilizando series de potencies, y definió con éxito logaritmo pa númberos negativos y complexos, espandiendo descomanadamente l'ámbitu de l'aplicación matemática de los llogaritmos.[37] Tamién definió la función esponencial pa númberos complexos, y afayó la so rellación coles funciones trigonométriques. Pa cualesquier númberu real φ, la fórmula d'Euler establez que la función esponencial complexa puede establecese por aciu la siguiente fórmula:
Siendo un casu especial de la fórmula (cuando = ), lo que se conoz como la identidá d'Euler:
Esta fórmula foi calificada por Richard Feynman como «la fórmula más reseñable en matemátiques», porque rellaciona les principales operaciones alxebraiques coles importantes constantes 0, 1, , y π, por aciu la rellación binaria más importante.[38] En 1988, los llectores de la revista especializada Mathematical Intelligencer votaron la fórmula como «la más bella fórmula matemática de la hestoria».[39] En total, Euler foi'l responsable del descubrimientu de trés de los cinco primeres fórmules de la resultancia de la encuesta.[39][40]
Amás d'eso, Euler ellaboró la teoría de les funciones trascendentes (aquelles que nun se basen n'operaciones alxebraiques) por aciu la introducción de la función gamma, ya introdució un nuevu métodu pa resolver ecuaciones de cuartu grau. Tamién afayó una forma pa calcular integrales con llendes complexes, no que sería d'equí p'arriba el modernu analís complexu, ya inventó el cálculu de variaciones incluyendo dientro del so estudiu a les que seríen llamaes les ecuaciones d'Euler-Lagrange.
Euler tamién foi pioneru nel usu de métodos analíticos pa resolver problemes teóricos de calter numbéricu. Con ello, Euler xunió dos rames separaes de les matemátiques pa crear un nuevu campu d'estudiu, la teoría analítica de númberos. Pa ello, Euler creó la teoría de les series hipergeométricas, les series q, les funciones hiperbóliques trigonométriques y la teoría analítica de fracciones continues. Por casu, demostró que la cantidá de númberos primos ye infinita utilizando la diverxencia de series harmóniques, y utilizó métodos analíticos pa consiguir una mayor información sobre cómo los númberos primos distribúyense dientro de la socesión de númberos naturales. El trabayu d'Euler nesta área llevaría al desenvolvimientu del teorema de los númberos primos.[41]
Teoría de númberos[editar | editar la fonte]
L'interés d'Euler na teoría de númberos vien de la influencia de Christian Goldbach, amigu so mientres la so estancia na Academia de San Petersburgu. Gran parte de los primeros trabayos d'Euler en teoría de númberos basar nos trabayos de Pierre de Fermat. Euler desenvolvió dalgunes de les idees d'esti matemáticu francés pero refugó tamién dalgunes de les sos conxetures.
Euler xunió la naturaleza de la distribución de los númberos primos coles sos idees del analís matemáticu. Demostró la diverxencia de la suma de los inversos de los númberos primos y, al faelo, afayó la conexón ente la función zeta de Riemann y los númberos primos. Esto conozse como'l productu d'Euler pa la función zeta de Riemann.
Euler tamién demostró les identidaes de Newton, el pequeñu teorema de Fermat, el teorema de Fermat sobre la suma de dos cuadraos y fixo importantes contribuciones al teorema de los cuatro cuadraos de Joseph-Louis de Lagrange. Tamién definió la función φ d'Euler que, pa tou númberu enteru positivu, cuantifica el númberu d'enteros positivos menores o iguales a n y coprimos con n. Más tarde, utilizando les propiedaes d'esta función, xeneralizó'l pequeñu teorema de Fermat a lo que se conoz como'l teorema d'Euler.
Contribuyó de manera significativa al entendimientu de los númberos perfectos, tema qu'esteló a los matemáticos dende los tiempos d'Euclides, y avanzó na investigación de lo que más tarde se concretaría nel teorema de los númberos primos. Los dos conceutos considérense teoremas fundamentales de la teoría de númberos, y les sos idees pavimentaron el camín del matemáticu Carl Friedrich Gauss.[42]
Nel añu 1772, Euler demostró que 231 - 1 = 2 147 483 647 ye un númberu primu de Mersenne. Esta cifra permaneció como'l númberu primu más grande conocíu hasta l'añu 1867.
Teoría de grafos y xeometría[editar | editar la fonte]

En 1736, Euler resolvió'l problema conocíu como problema de les pontes de Königsberg.[43] La ciudá de Königsberg, en Prusia Oriental (anguaño Kaliningráu, en Rusia), taba alcontrada nel ríu Pregel, ya incluyía dos grandes islles que taben coneutaes ente elles por una ponte, y colos dos riberes del ríu por aciu seis puente (siete puente en total). El problema que se plantegaben los sos habitantes consistía en decidir si yera posible siguir un camín, y cómo faelo, que cruciara toles pontes una sola vegada y que rematara llegando al puntu de partida. Euler llogró demostrar matemáticamente que nun lo hai. Nun hai lo que se denomina güei un ciclu euleriano nel grafo que modela'l terrén), por cuenta de que'l númberu de pontes ye impar en más de dos de los bloques (representaos por vértices nel grafo correspondiente).
A esta solución considerar el primer teorema de teoría de grafos y de grafos planares.[43] Euler tamién introdució'l conceutu conocíu como carauterística d'Euler del espaciu, y una fórmula que rellacionaba'l númberu de llaos, vértices y cares d'un polígonu convexu con esta constante. El teorema de poliedros d'Euler, que básicamente consiste en buscar una rellación ente númberu de cares, arestes y vértices nos poliedros. Utilizó esta idea pa demostrar que nun esistíen más poliedros regulares que los sólidos platónicos conocíos hasta entós. L'estudiu y la xeneralización d'esta fórmula, especialmente por Cauchy[44] y L'Huillier,[45] supunxo l'orixe de la topoloxía.[46][47]
Dientro del campu de la xeometría analítica afayó amás que trés de los puntos notables d'un triángulu —baricentru, ortocentro y circuncentro— podíen obedecer a una mesma ecuación, esto ye, a una mesma recta. A la recta que contién el baricentru, ortocentro y circuncentro denominar «Recta d'Euler» nel so honor.
Matemática aplicada[editar | editar la fonte]
Dalgunos de los mayores ésitos d'Euler fueron na resolución de problemes del mundu real al traviés del analís matemáticu, no que se conoz como matemática aplicada, y na descripción de numberoses aplicaciones de los númberos de Bernoulli, les series de Fourier, los diagrames de Venn, el númberu d'Euler, les constantes e y π, les fracciones continues y les integrales. Integró'l cálculu diferencial de Leibniz col métodu de flusión de Newton, y desenvolvió ferramientes que faíen más fácil l'aplicación del cálculu a los problemes físicos. Euler yá emplegaba les series de Fourier primero que'l mesmu Fourier afayar y les ecuaciones de Lagrange del cálculu variacional, les ecuaciones d'Euler-Lagrange.
Fixo grandes meyores na meyora de los aproximamientos numbéricos pa resolver integrales, inventando lo que se conoz como los aproximamientos d'Euler. Les más notables d'estos aproximamientos son el métodu d'Euler pa resolver ecuaciones diferenciales ordinaries, y la fórmula d'Euler-Maclaurin. Esti métodu consiste en dir amontando pasu a pasu la variable independiente y topando la siguiente imaxe cola derivada. Tamién facilitó l'usu d'ecuaciones diferencialessobremanera por aciu la introducción de la constante d'Euler-Mascheroni:
Per otru llau, unu de los intereses más llamativos d'Euler foi l'aplicación de les idees matemátiques sobre la música. En 1739 escribió la so obra Tentamen novae theoriae musicae, esperando con ello poder incorporar l'usu de les matemátiques a la teoría musical. Esta parte del so trabayu, sicasí, nun atraxo demasiada atención del públicu, y aportó a descrita como demasiáu matemática pa los músicos y demasiáu musical pa los matemáticos.[48]
Ecuaciones d'Euler d'orde n[editar | editar la fonte]
Son les que siguen:
- , ecuación d'orde n y siendo les constantes.[49]
- ye una ecuación de segundu orde con coeficientes variables.[50]
Física y astronomía[editar | editar la fonte]
Euler ayudó a desenvolver la ecuación de la curva elástica, que se convirtió na pilastra de la inxeniería. Amás de aplicar con ésitu les sos ferramientes analítiques a los problemes de mecánica clásica, Euler tamién les aplicó sobre los problemes de los movimientos de los astros celestes. El so trabayu en astronomía foi reconocíu por aciu dellos premios de l'Academia de Francia a lo llargo de la so carrera, y les sos apurras nesi campu inclúin cuestiones como la determinación con gran exactitú de les órbites de los cometes y d'otros cuerpos celestes, amontando l'entendimientu de la naturaleza de los primeres, o'l cálculu del paralax solar. Formuló siete ley o principios fundamentales sobre la estructura y dinámica del Sistema Solar y afirmó que los distintos cuerpos celestes y planetarios rotan alredor del Sol siguiendo una órbita de forma elíptica. Los sos cálculos tamién contribuyeron al desenvolvimientu de tables de llargor más exactes pa la navegación.[51] Tamién publicó trabayos sobre'l movimientu de la Lluna.
Amás, Euler llevó a cabu importantes contribuciones nel área de la óptica. Nun taba acordies coles teoríes de Newton sobre la lluz, desenvueltes na so obra Opticks, y que yeren la teoría prevalente naquel momentu. Los sos trabayos sobre óptica desenvueltos na década de 1740 ayudaron a que la nueva corriente que proponía una teoría de la lluz en forma d'onda, propuesta por Christiaan Huygens, convertir na teoría hexemónica. La nueva teoría caltendría esi estatus hasta'l desenvolvimientu de la teoría cuántica de la lluz.[52]
Nel campu de la mecánica Euler, nel so tratáu de 1739, introdució explícitamente los conceutos de partícula y de masa puntual y la notación vectorial pa representar la velocidá y l'aceleración, lo que sentaría les bases de too l'estudiu de la mecánica hasta Lagrange. Nel campu de la mecánica del sólidu ríxidu definió los llamaos «trés ángulos d'Euler pa describir la posición» y publicó'l teorema principal del movimientu, según el cual siempres esiste una exa de rotación instantáneu, y la solución del movimientu llibre (consiguió estenar los ángulos en función del tiempu).
En hidrodinámica estudió'l fluxu d'un fluyíu ideal incompresible, detallando les ecuaciones d'Euler de la hidrodinámica.
Adelantrándose más de cien años a Maxwell previo'l fenómenu de la presión de radiación, fundamental na teoría unificada del electromagnetismu. Nos cientos de trabayos d'Euler atópense referencies a problemes y cuestiones tremendamente avanzaes pal so tiempu, que nun taben al algame de la ciencia de la so dómina.
Lóxica[editar | editar la fonte]
Nel campu de la lóxica, atribuyir a Euler l'usu de curves zarraes pa ilustrar el razonamientu siloxísticu (1768). Les representaciones d'esti tipu reciben el nome de diagrames d'Euler.[53]
Arquiteutura ya inxeniería[editar | editar la fonte]
Nesti campu, Euler desenvolvió la llei que lleva'l so nome sobre'l pandeo de soportes verticales y xeneró una nueva caña d'inxeniería colos sos trabayos sobre la carga crítica de les columnes.
Creencies relixoses y filosófiques[editar | editar la fonte]
Euler y el so amigu Daniel Bernoulli oponer al monismu de Leibniz y a la corriente filosófica representada por Christian Wolff. Euler aportunaba en que la conocencia basar en parte na esistencia de lleis cuantitatives precises, daqué que'l monismu y les teoríes filosófiques de Wolff nun yeren capaces d'aprovir. Los sos enclinos relixosos tamién pueden contribuyir a que-y ofendiera esi tipu de doctrines, hasta'l puntu de que llegó a catalogar les idees de Wolff como «paganes y atees».[54]
Gran parte de la conocencia que tenemos de les creencies relixoses d'Euler deducir de la so obra Cartes a una Princesa alemana, lo mesmo que de un trabayu anterior llamáu Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister (n'español, Defensa de la revelación divina frente a les oxeciones de los llibrepensadores). Estos trabayos amuesen a Euler como un cristianu convencíu que defendía la interpretación lliteral de la Biblia (por casu, la so obra Rettung yera principalmente un discutiniu en defensa de la inspiración divina de les escritures).[55]
Obra[editar | editar la fonte]

Euler cuenta con una extensísima bibliografía, nesta seición puede atopase dalguna referencia sobre dalgunes de les sos obres más conocíes o importantes.
- Mechanica, sive motus scientia analytica exposita[56] (1736)
- Tentamen novae theoriae musicae (1739)
- Solutio problematis ad geometriam situs pertinentis (1741)
- Methodus inveniendi llinies curves maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744).
- Introductio in Analysis Infinitorum (1748)
- Institutiones Calculi Differentialis (1765)
- Theoria motus corporum solidorum seu rigidorum (1765)
- Institutiones Calculi Integralis (1768-1770)
- Vollständige Anleitung zur Álxebra[57] (1770)
- Lettres à une Princesse d'Allemagne (Cartes a una Princesa alemana)[58] (1768–1772).
En 1911, l'Academia Suiza de les Ciencies empezó a publicar una coleición definitiva de los trabayos d'Euler titulada Opera Omnia.[31] Esiste un plan pa l'ampliación de la obra a la publicación de la correspondencia (nel añu 2008 publicáronse yá tres volúmenes de correspondencia) y los manuscritos d'Euler, anque nun s'especificó nenguna fecha pa la so edición.[59]
Ver tamién[editar | editar la fonte]
Notes[editar | editar la fonte]
- ↑ Afirmao en: Gemeinsame Normdatei. Data de consulta: 10 avientu 2014. Llingua de la obra o nome: alemán. Autor: Biblioteca Nacional d'Alemaña.
- ↑ Biblioteca Nacional de Francia. «autoridaes BNF» (francés). Consultáu'l 10 ochobre 2015.
- ↑ 3,0 3,1 3,2 Identificador DHS: 018751.
- ↑ Afirmao en: Gemeinsame Normdatei. Data de consulta: 30 avientu 2014. Llingua de la obra o nome: alemán. Autor: Biblioteca Nacional d'Alemaña.
- ↑ Afirmao en: MacTutor History of Mathematics archive. Data de consulta: 22 agostu 2017.
- ↑ «Q21001800» (en rusu). Russian Biographical Dictionary, Volume 24.
- ↑ 7,0 7,1 Biblioteca Nacional de Francia. «autoridaes BNF» (francés). Consultáu'l 17 febreru 2019.
- ↑ Biblioteca Nacional de Francia. «autoridaes BNF» (francés). Consultáu'l 10 ochobre 2015.
- ↑ 9,0 9,1 URL de la referencia: https://www.amacad.org/sites/default/files/academy/multimedia/pdfs/publications/bookofmembers/ChapterE.pdf.
- ↑ Afirmao en: Encyclopædia Britannica. Autor: Andrew Bell. Editorial: Encyclopædia Britannica. Llingua de la obra o nome: inglés británicu.
- ↑ 11,0 11,1 Afirmao en: MacTutor History of Mathematics archive.
- ↑ Afirmao en: NNDB. Llingua de la obra o nome: inglés.
- ↑ Afirmao en: www.accademiadellescienze.it. Accademia delle Scienze di Torino ID: leonhard-euler. Data de consulta: 1r avientu 2020. Llingua de la obra o nome: italianu.
- ↑ 14,0 14,1 Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America, páx. 17.
- ↑ 15,0 15,1 15,2 Finkel, B.F. (1897). «Biography- Leonard Euler». The American Mathematical Monthly 4 (12): páxs. 300.
- ↑ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America, páx. xiii. «Lisez Euler, lisez Euler, c'est notre maître à tous.»
- ↑ James, Ioan (2002). Remarkable Mathematicians: From Euler to von Neumann. Cambridge, páx. 2. ISBN 0-521-52094-0.
- ↑ «Traducción al inglés por Ian Bruce del Ph.D d'Euler». Consultáu'l 8 d'abril de 2005.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 156.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 125.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 127.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 124.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 128–129.
- ↑ Fuss, Nicolas. «Eulogy of Euler by Fuss».
- ↑ «Institutiones calculi differentialis (traducción n'inglés)». Consultáu'l 8 d'abril de 2008.
- ↑ 26,0 26,1 26,2 Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America, páx. xxiv–xxv.
- ↑ Frederick II of Prussia; Traducción: Richard Aldington (1927). Letters of Voltaire and Frederick the Great, Letter H 7434, 25 January 1778. New York: Brentano's.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 154–155.
- ↑ «Biografía d'Euler». Consultáu'l 10 d'abril de 2005.
- ↑ Marquis de Condorcet. «Eulogy of Euler - Condorcet».
- ↑ 31,0 31,1 Opera Omnia en http://www.eulerarchive.org
- ↑ Mónica Salomone (26 d'avientu de 2007). «Entrevista nel periódicu El País a Hanspeter Kraft». Consultáu'l 8 d'abril de 2008. Entrevista nel periódicu El País a Hanspeter Kraft
- ↑ Hestoria del Sudoku
- ↑ Boyer, Carl B.; Uta C. Merzbach. A History of Mathematics. John Wiley & Sons, páx. 439–445. ISBN 0-471-54397-7.
- ↑ Wolfram, Stephen. «Mathematical Notation: Past and Future».
- ↑ 36,0 36,1 Wanner, Gerhard; Harrier, Ernst (March de 2005). Analysis by its history, 1st, Springer, páx. 62.
- ↑ Boyer, Carl B.; Merzbach, Uta C.. A History of Mathematics. John Wiley & Sons, páx. 439–445. ISBN 0-471-54397-7.
- ↑ Feynman, Richard. «Chapter 22: Algebra», The Feynman Lectures on Physics: Volume I, páx. p.10.
- ↑ 39,0 39,1 Wells, David (1990). «Are these the most beautiful?». Mathematical Intelligencer 12 (3): páxs. 37–41.
- ↑ Wells, David (1988). «Which is the most beautiful?». Mathematical Intelligencer 10 (4): páxs. 30–31.
Ver tamién *Peterson, Ivars. «The Mathematical Tourist». Archiváu dende l'orixinal, el 31 de marzu de 2007. Consultáu'l marzu de 2008. - ↑ Dunham, William (1999). «3,4», Euler: The Master of Us All. The Mathematical Association of America.
- ↑ Dunham, William (1999). «1,4», Euler: The Master of Us All. The Mathematical Association of America.
- ↑ 43,0 43,1 Alexanderson, Gerald (July 2006). «Euler and Königsberg's bridges: a historical view». Bulletin of the American Mathematical Society.
- ↑ Cauchy, A.L. (1813). «Recherche sur les polyèdres—premier mémoire». Journal de l'Ecole Polytechnique 9 (Cahier 16): páxs. 66–86.
- ↑ L'Huillier, S.-A.-J. (1861). «Mémoire sur la polyèdrométrie». Annales de Mathématiques 3: páxs. 169–189.
- ↑ Marta Macho Stadler. «¿Qué ye la topoloxía?». Archiváu dende l'orixinal, el 9 de xunu de 2004. Consultáu'l 10 d'abril de 2005.
- ↑ David Garro Moreno. «Historia de la topoloxía». Consultáu'l 10 d'abril de 2005.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 144–145.
- ↑ Makárenko y otros. Problemes d'ecuaciones diferenciales ordinaries
- ↑ Derick- Grossman. Ecuaciones diferenciales con aplicaciones
- ↑ Youschkevitch, A P; Biography in Dictionary of Scientific Biography (New York 1970–1990).
- ↑ Home, R.W. (1988). «Leonhard Euler's 'Anti-Newtonian' Theory of Light». Annals of Science 45 (5): páxs. 521–533.
- ↑ Baron, M. Y.; A Note on The Historical Development of Logic Diagrams. The Mathematical Gazette: The Journal of the Mathematical Association. Vol LIII, non. 383 May 1969.
- ↑ Calinger, Ronald (1996). «Leonhard Euler: The First St. Petersburg Years (1727–1741)». Historia Mathematica 23 (2): páxs. 153–154.
- ↑ Euler, Leonhard (1960). «Rettung der Göttlichen Offenbahrung Gegen die Einwürfe der Freygeister». Leonhardi Euleri Opera Omnia (series 3) 12.
- ↑ «Mechanica, sive motus scientia analytica exposita» (francés). Consultáu'l 8 d'abril de 2008.
- ↑ «Vollständige Anleitung zur Algebra» (francés). Consultáu'l 8 d'abril de 2008.
- ↑ «Lettres à une Princesse d'Allemagne t. 1» (francés). Consultáu'l 8 d'abril de 2008. «Lettres à une Princesse d'Allemagne t. 2» (francés). Consultáu'l 8 d'abril de 2008. «Lettres à une Princesse d'Allemagne t. 3» (francés). Consultáu'l 8 d'abril de 2008.
- ↑ «Información sobre la Opera Omnia y otres publicaciones de trabayos d'Euler». Consultáu'l 8 d'abril de 2008.
Otres llectures[editar | editar la fonte]
- Lexikon der Naturwissenschaftler, 2000. Heidelberg: Spektrum Akademischer Verlag.
- Demidov, S.S., 2005, «Treatise on the differential calculus» en Grattan-Guiness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 191-98.
- Dunham, William (1999) Euler: The Master of Us All, Washington: Mathematical Association of America. ISBN 0-88385-328-0.
- Euler, Leonhard (1768) - Mínguez Pérez, Carlos (ed.) (1990) Cartes a una Princesa d'Alemaña sobre diverses temes de Física y Filosofía, Prenses de la Universidá de Zaragoza, ISBN 84-7733-145-6
- Fraser, Craig G., 2005, «Book on the calculus of variations» en Grattan-Guiness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 168-80.
- Gladyshev, Georgi, P (2007) «Leonhard Euler's methods and ideas live on in the thermodynamic hierarchical theory of biological evolution», International Journal of Applied Mathematics & Statistics (IJAMAS) 11 (N07), Special Issue on Leonhard Paul Euler's: Mathematical Topics and Applications (M. T. A.).
- W. Gautschi (2008). «Leonhard Euler: his life, the man, and his works». SIAM Review 50 (1): páxs. 3–33. doi:.
- Heimpell, Hermann, Theodor Heuss, Benno Reifenberg (editors). 1956. Die großen Deutschen, volume 2, Berlin: Ullstein Verlag.
- Krus, D.J (2001) «Is the normal distribution due to Gauss? Euler, his family of gamma functions, and their place in the history of statistics», Quality and Quantity: International Journal of Methodology, 35: 445-46.
- Nahin, Paul (2006) Dr. Euler's Fabulous Formula, New Jersey: Princeton, ISBN 978-0-691-11822-2
- Reich, Karin, 2005, «Introduction' to analysis» en Grattan-Guiness, I., ed., Landmark Writings in Western Mathematics. Elsevier: 181-90.
- Sandifer, Edward C (2007), The Early Mathematics of Leonhard Euler, Washington: Mathematical Association of America. ISBN 0-88385-559-3
- Simmons, J (1996) The giant book of scientists: The 100 greatest minds of all time, Sydney: The Book Company.
- Singh, Simon (1997). Fermat's last theorem, Fourth Ta: New York, ISBN 1-85702-669-1
- Thiele, Rüdiger (2005). «The mathematics and science of Leonhard Euler», in Mathematics and the Historien's Craft: The Kenneth O. May Lectures, G. Van Brummelen and M. Kinyon (eds.), CMS Books in Mathematics, Springer Verlag. ISBN 0-387-25284-3.
- «A Tribute to Leohnard Euler 1707-1783». Mathematics Magazine 56 (5). November 1983.
Enllaces esternos[editar | editar la fonte]
 Wikimedia Commons tien conteníu multimedia tocante a Leonhard Euler.
Wikimedia Commons tien conteníu multimedia tocante a Leonhard Euler. Wikiquote tien frases célebres suyes o que faen referencia a Leonhard Euler.
Wikiquote tien frases célebres suyes o que faen referencia a Leonhard Euler.- The Euler Archive
- O'Connor, John J.; Robertson, Edmund F., «Leonhard Euler» (n'inglés), MacTutor History of Mathematics archive, Universidá de Saint Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Euler.html.
- Artículu na Encyclopedia Britannica
- How Euler did it Páxina web que contién esplicaciones sobre cómo Euler resolvió diversos problemes.
- Euler Archive
- Euler Committee of the Swiss Academy of Sciences
- Tricentenario d'Euler (añu 2007)
- The Euler Society
- Leonhard Euler Congress 2007 — San Petersburgu, Rusia.
- "Euler - 300th anniversary lecture", discursu pronunciáu por Robin Wilson en Gresham College, el 9 de mayu de 2007.
- Project Euler
- Árbol de familia d'Euler
- 1000 artículos que toa Wikipedia habría de tener
- Homes
- Wikipedia:Artículos con plantíes de notes d'encabezamientu enllaciando a páxines que nun esisten
- Persones nacíes en 1707
- Persones finaes en 1783
- Wikipedia:Revisar traducción
- Físicos y físiques de Suiza
- Matemáticos y matemátiques de Suiza
- Teóricos y teóriques de númberos
- Xeómetres



















