Númberu primu
| Númberu primu | ||||
|---|---|---|---|---|
| tipu de númberu | ||||
|
entero libre de cuadrados (es) | ||||
 | ||||
| ||||

En matemátiques, un númberu primu ye un númberu natural mayor que 1 que tien namái dos divisores distintos: él mesmu y el 1.[1][2] Otra manera, los númberos compuestos son los númberos naturales que tienen dalgún divisor natural amás de sí mesmos y del 1 y poro, pueden factorizarse. El númberu 1, por conveniu, nun se considera nin primu nin compuestu.
Los 168 númberos primos menores de 1000 son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997... (socesión A000040 n'OEIS).
La propiedá de ser primu denominar primalidá. Dacuando fálase de númberu primu impar pa referise a cualquier númberu primu mayor que 2, yá que este ye l'únicu númberu primu par. Dacuando se denota el conxuntu de tolos númberos primos por . Na teoría alxebraica de númberos, a los númberos primos conózse-yos como númberos racionales primos pa estremalos de los númberos gaussianos primos.[3]
L'estudiu de los númberos primos ye una parte importante de la teoría de númberos, caña de les matemátiques que trata les propiedaes, básicamente aritmétiques,[4] de los númberos enteros. Los númberos primos tán presentes en delles conxetures centenaries tales como la hipótesis de Riemann y la conxetura de Goldbach, resuelta pol peruanu Harald Helfgott na so forma débil.
La distribución de los númberos primos ye una tema recurrente d'investigación na teoría de númberos: si considérense númberos individuales, los primos paecen tar distribuyíos aleatoriamente, pero la distribución global» de los númberos primos sigue lleis bien definíes.
Historia de los númberos primos[editar | editar la fonte]
L'Oriente prehelénicu[editar | editar la fonte]

Les mozquetes presentes nel güesu d'Ishango, que data de hai más de 20.000 años (anterior por tanto a l'apaición de la escritura) y que foi topáu pol arqueólogu Jean de Heinzelin de Braucourt,[5] paecen aisllar cuatro números primos: 11, 13, 17 y 19. Dellos arqueólogos interpreten esti fechu como la prueba de la conocencia de los númberos primos. Con tou, esisten bien pocos afayos que dexen discernir les conocencies que tenía realmente l'home d'aquella dómina.[6]
Numberoses tablillas de magre secu atribuyíes a les civilizaciones que se fueron asocediendo en Mesopotamia a lo llargo del II mileniu e.C. amuesen el resolución de problemes aritméticos y atestigüen les conocencies de la dómina. Los cálculos riquíen conocer los inversos de los naturales, que tamién se toparon en tablillas.[7] Nel sistema sexaxesimal qu'emplegaben los babilonios pa escribir los númberos, los inversos de los divisores de potencies de 60 (númberos regulares) calcúlense fácilmente; por casu, estremar ente 24 equival a multiplicar por 150 (2·60+30) y correr la coma sexaxesimal dos llugares. La conocencia matemática de los babilonios precisaba una sólida comprensión de la multiplicación, la división y la factorización de los naturales.
Nes matemátiques exipcies, el cálculu de fracciones riquía conocencies sobre les operaciones, la división de naturales y la factorización. Los exipcios namái operaben coles llamaes fracciones exipcies, suma de fracciones unitaries, esto ye, aquelles que'l so numberador ye 1, como , polo que les fracciones de numberador distintu de 1 escribíense como suma d'inversos de naturales, a ser posible ensin repetición en llugar de .[8] Ye por ello que, en cierta manera, teníen que conocer o albidrar los númberos primos.[9]
Antigua Grecia[editar | editar la fonte]

La primer prueba indiscutible de la conocencia de los númberos primos remontar a alredor del añu 300 e. C. y atópase nos Elementos d'Euclides (tomos VII a IX). Euclides define los númberos primos, demuestra qu'hai infinitos d'ellos, define'l máximu común divisor y el mínimu común múltiplu y apurre un métodu pa determinalos qu'anguaño se conoz como l'algoritmu d'Euclides. Los Elementos contienen coles mesmes el teorema fundamental de l'aritmética y la manera de construyir un númberu perfectu a partir d'un númberu primu de Mersenne.
La peñerada de Eratóstenes, atribuyida a Eratóstenes de Cirene, ye un métodu senciellu que dexa atopar númberos primos. Anguaño, sicasí, los mayores númberos primos que s'atopen cola ayuda d'ordenadores empleguen otros algoritmos más rápidos y complexos.
Dende la dómina de la renacencia[editar | editar la fonte]

Dempués de les matemátiques griegues, hubo poques meyores nel estudiu de los númberos primos hasta'l sieglu XVII. En 1640 Pierre de Fermat estableció (anque ensin demostración) el pequeñu teorema de Fermat, darréu demostráu por Leibniz y Euler. Ye posible que muncho primero se conociera un casu especial de dichu teorema en China.
Fermat conxeturó que tolos númberos de la forma 22n+1 yeren primos (por cuenta de lo cual conocer como númberos de Fermat) y verificó esta propiedá hasta n = 4 (esto ye, 216 + 1). Sicasí, el númberu de Fermat 232 + 1 ye compuestu (unu de los sos factores primos ye 641), como demostró Euler. Ello ye que hasta los nuesos díes nun se conoz nengún númberu de Fermat que sía primu amás de los que yá conocía'l mesmu Fermat.
El monxu francés Marin Mersenne investigó los númberos primos de la forma 2p − 1, con p primu. Nel so honor, conocer como númberos de Mersenne.
Nel trabayu de Euler en teoría de númberos atopen munchos resultancies que concernen a los númberos primos. Demostró la diverxencia de la serie , y en 1747 demostró que tolos númberos perfectos pares son de la forma 2p-1(2p - 1), onde'l segundu factor ye un númberu primu de Mersenne. Créese que nun esisten númberos perfectos impares, pero inda ye una cuestión abierta.
A empiezos del sieglu XIX, Legendre y Gauss conxeturaron de forma independiente que, cuando n tiende a infinitu, el númberu de primos menores o iguales que n ye asintótico a , onde ln(n) ye'l llogaritmu natural de n. Les idees que Bernhard Riemann afiguró nun trabayu de 1859 sobre la función zeta describieron el camín que conduciría a la demostración del teorema de los númberos primos. Hadamard y De la Vallée-Poussin, cada unu por separáu, dieron forma a esti esquema y consiguieron demostrar el teorema en 1896.
Anguaño nun se comprueba la primalidá d'un númberu por divisiones socesives, siquier non si'l númberu ye relativamente grande.
Mientres el sieglu XIX desenvolviéronse algoritmos pa saber si un númberu ye primu o non factorizando dafechu'l númberu siguiente (p+1) o l'anterior (p-1). Dientro del primer casu atópase'l test de Lucas-Lehmer, desenvueltu a partir de 1856. Dientro del segundu casu atópase'l test de Pépin pa los númberos de Fermat (1877). El casu xeneral de test de primalidá cuando'l númberu darréu anterior atópase dafechu factorizado denominar test de Lucas.
Darréu atopáronse algoritmos de primalidá con solo llograr una factorización parcial de p+1 o p-1. Exemplos d'estos algoritmos son el test de Proth (desenvueltu alredor de 1878) y el test de Pocklington (1914). Nestos algoritmos ríquese que'l productu de los factores primos conocíos de p-1 sía mayor que'l raigañu cuadráu de p. Más apocayá, en 1975, Brillhart, Lehmer y Selfridge desenvolvieron el test BLS de primalidá que solo rique que dichu productu sía mayor que'l raigañu cúbicu de p. El meyor métodu conocíu d'esta clase ye'l test de Konyagin y Pomerance del añu 1997, que rique que dichu productu sía mayor que p3/10.[10][11]
A partir de la década de 1970 dellos investigadores afayaron algoritmos pa determinar si cualquier númberu ye primu o non con complexidá subexponencial, lo que dexa realizar tests en númberos de miles de díxitos, anque son muncho más lentos que los métodos anteriores. Exemplos d'estos algoritmos son el test APRT-CL (desenvueltu en 1979 por Adleman, Pomerance y Rumely, con meyores introducíes por Cohen y Lenstra en 1984), onde s'usen los factores de pm-1, onde l'esponente m depende del tamañu del númberu que la so primalidá deseyar verificar, el test de primalidá por curves elíptiques (desenvueltu en 1986 por S. Goldwasser, J. Kilian y ameyoráu por A. O. L. Atkin), qu'apurre un certificáu consistente nuna serie de númberos que dexa dempués confirmar rápido si'l númberu ye primu o non. El desenvolvimientu más recién ye'l test de primalidá AKS (2002), que magar la so complexidá ye polinómica, pa los númberos que puede remanar la teunoloxía actual ye'l más lentu de los trés.
Mientres enforma tiempu, pensábase que l'aplicación de los númberos primos yera bien llindada fora de la matemática pura.[12][13] Esto camudó nos años 1970 col desenvolvimientu de la criptografía de clave pública, na que los númberos primos formaben la base de los primeros algoritmos, tales como l'algoritmu RSA.
Dende 1951, el mayor númberu primu conocíu siempres foi afayáu cola ayuda d'ordenadores. La busca de númberos primos cada vez mayores amenó interés inclusive fora de la comunidá matemática. Nos últimos años ganaron popularidá proyeutos de computación distribuyida tales como'l GIMPS, mientres los matemáticos siguen investigando les propiedaes de los númberos primos.
Aprimalidá del númberu 1[editar | editar la fonte]
La cuestión alrodiu de si'l númberu 1 debe o nun considerase primu ta basada na convención. Dambes postures tienen les sos ventayes y los sos inconvenientes. Ello ye que hasta'l sieglu XIX, los matemáticos n'el so mayoría considerar primu. Munchos trabayos matemáticos siguen siendo válidos a pesar de considerar el 1 como un númberu primu, como, por casu, el de Stern y Zeisel. La llista de Derrick Norman Lehmer de númberos primos hasta'l 10.006.721, reimpresa hasta l'añu 1956[14] empezaba col 1 como primer númberu primu.[15]
Anguaño, la comunidá matemática inclinar por nun considerar al 1 na llista de los númberos primos. Esta convención, por casu, dexa una formulación bien económica del teorema fundamental de l'aritmética: «tou númberu natural tien una representación única como productu de factores primos, salvo l'orde».[16][17] Amás, los númberos primos tienen numberoses propiedaes de les qu'escarez el 1, tales como la rellación del númberu col valor correspondiente de la función φ de Euler o la función divisor.[18] Cabo tamién la igualdá pa tou enteru positivu, , lo que dexaría dicir que tien factores.[19]
Propiedaes de los númberos primos[editar | editar la fonte]
Teorema fundamental de l'aritmética[editar | editar la fonte]
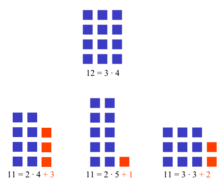
El teorema fundamental de l'aritmética establez que tou númberu natural tien una representación única como productu de factores primos, salvo l'orde. Un mesmu factor primu puede apaecer delles vegaes. El 1 represéntase entós como un productu vacíu.
Puede considerase que los númberos primos son los lladriyos» colos que se constrúi cualquier númberu natural. Por casu, puede escribise el númberu 23.244 como productu de 2²·3·13·149, y cualesquier otra factorización del 23.244 como productu de númberos primos va ser idéntica sacante pol orde de los factores.
La importancia d'esti teorema ye una de les razones pa escluyir el 1 del conxuntu de los númberos primos. Si almitiera'l 1 como númberu primu, l'enunciáu del teorema riquiría aclaraciones adicionales.
A partir d'esta unicidá na factorización en factores primos desenvuélvense otros conceutos bien utilizaos en matemátiques, tales como'l mínimu común múltiplu, el máximu común divisor y la coprimalidá de dos o más númberos. Asina, * El mínimu común múltiplu de dos o más númberos ye'l menor de los múltiplos comunes de toos ellos. Pa calculalo, descompónense los númberos en factores primos y tómense los factores comunes y non comunes col so máximu esponente. Por casu, el mínimu común múltiplu de 10=2·5 y 12=2²·3 ye 60=2²·3·5.
- El máximu común divisor de dos o más númberos ye'l mayor de los divisores comunes de toos ellos. Ye igual al productu de los factores comunes col so mínimu esponente. Nel exemplu anterior, el máximu común divisor de 10 y 12 ye 2.
- Finalmente, dos o más númberos son coprimos, o primos ente sigo, si nun tienen nengún factor primu común; esto ye, si'l so máximu común divisor ye 1. Un númberu primu ye, asina, coprimo con cualquier númberu natural que nun sía múltiplu d'él mesmu.
Otres propiedaes[editar | editar la fonte]
- Na so escritura nel sistema de numberación decimal, tolos númberos primos, salvo'l 2 y el 5, tien como'l guarismu de les unidaes unu d'estos: 1, 3, 7 o 9. Polo xeneral, en cualquier sistema de numberación, tolos númberos primos salvu un númberu finito acaben nuna cifra que ye coprima cola base.
- De lo anterior deduzse que tolos númberos primos salvu'l 2 son de la forma 4n + 1 o bien 4n + 3. Igualmente, tolos númberos primos salvu'l 2 y el 3 son de la forma 6n + 1 o 6n - 1.
- Lema d'Euclides: Si p ye un númberu primu y divisor del productu de númberos enteros ab, entós p ye divisor de a o de b.
- Pequeñu teorema de Fermat: Si p ye primu y a ye dalgún númberu natural distintu de 1, entós ap - a ye divisible por p.
- Si p ye primu distintu de 2 y 5, siempres ye un númberu periódicu na so representación decimal, de periodu p − 1 o un divisor de p − 1. Esto puédese deducir direutamente a partir del pequeñu teorema de Fermat. espresáu en base q (en llugar d'en base 10) tien propiedaes similares, siempres que p nun sía un factor primu de q.
- Teorema de Wilson: Un númberu natural n > 1 ye primu si y solu si el factorial (n - 1)! + 1 ye divisible por n. Coles mesmes, un númberu natural n > 4 ye compuestu si y solu si (n - 1)! ye divisible por n.
- La carauterística de too cuerpu ye, o bien cero, o bien un númberu primu.
- Primer teorema de Sylow: Si G ye un grupu finito, p primu y pn ye la mayor potencia de p qu'estrema'l orde de G. Entós, esiste un subgrupu de G d'orde pn.
- Teorema de Cauchy: Si G ye un grupu finito y p ye un númberu primu qu'estrema al orde de G, entós G contién un elementu d'orde p.
- La constante de Copeland-Erdős 0,235711131719232931374143…, llograda por concatenación de los númberos primos nel sistema decimal, ye un númberu irracional.
- El valor de la función zeta de Riemann en cada puntu del planu complexu dase como una continuación meromorfa d'una función definida por un productu sobre'l conxuntu de tolos primos pa Re(s) > 1:
- Na rexón onde ye converxente, esti productu indexado polos númberos primos puede calculase, llográndose diversos valores, dalgunos d'ellos importantes en teoría de númberos. Los dos primeros son:
- (Correspondiente a la serie harmónica, rellacionáu cola infinitud de númberos primos).
- (Correspondiente al problema de Basilea).
- Polo xeneral ye un númberu racional cuando n ye un númberu enteru positivu par.
- L'aniellu ye un cuerpu si y solu si p ye primu. Equivalentemente: p ye primu si y solu si φ(p) = p − 1.
- Si p > 1, el polinomiu x p-1+x p-2+ ··· + 1 ye irreducible sobre si y solu si p ye primu.
- Un númberu natural n ye primu si y solu si'l n-ésimo polinomiu de Chebyshov de la primer especie Tn(x), estremáu ente x, ye irreducible en . Amás, Tn(x) ≡ xn si y solu si n ye primu.
- Non tou númberu primu ye un númberu gaussiano primu; tal el casu de 2, que como enteru gaussiano almite la descomposición don de la norma de ye 2, polo tanto nun ye unidá en Z[i].
- Los númberos primos de la forma son igual a la suma de dos cuadraos perfectos; polo que nun son númberos gaussianos primos. En cuantes que los númberos primos de la forma sí son númberos gaussianos primos.
- Tou númberu racional primu ye un númberu gaussiano enteru, ensin ser necesariamente númberu gaussiano primu.[20]
Númberos primos y funciones aritmétiques[editar | editar la fonte]
Les funciones aritmétiques, esto ye, funciones reales o complexes, definíes sobre un conxuntu de númberos naturales, desempeñen un papel crucial na teoría de númberos. Les más importantes son les funciones multiplicatives, que son aquelles funciones f nes cualos, pa cada par de númberos coprimos (a,b) tiense :.
Dellos exemplos de funciones multiplicatives son la función φ de Euler, qu'a cada n acomuña'l númberu d'enteros positivos menores y coprimos con n, y les funciones τ y σ, qu'a cada n acomuñen respeutivamente el númberu de divisores de n y la suma de toos ellos. El valor d'estes funciones nes potencies de númberos primos ye :,
- , :..
Gracies a la propiedá que les define, les funciones aritmétiques pueden calculase fácilmente a partir del valor que tomen nes potencies de númberos primos. Ello ye que dau un númberu natural n de factorización
tiense que :
colo que se recondució'l problema de calcular f(n) al de calcular f sobre les potencies de los númberos primos qu'estremen n, valores que son xeneralmente más fáciles de llograr por aciu una fórmula xeneral. Por casu, pa conocer el valor de la función φ sobre n=450=2·3²·5² basta con calcular
- .
Carauterístiques del conxuntu de los númberos primos[editar | editar la fonte]
Infinitud de los númberos primos[editar | editar la fonte]
Esisten infinitos númberos primos. Euclides realizó la primera demostración alredor del añu 300 e. C. nel llibru IX de la so obra Elementos[21] Una adautación común d'esta demostración orixinal sigue asina: Tómase un conxuntu arbitrariu pero finito de númberos primos p1, p2, p3, ···, pn, y considérase el productu de toos ellos más unu, . Esti númberu ye obviamente mayor que 1 y distintu de tolos primos pi de la llista. El númberu q puede ser primu o compuestu. Si ye primu vamos tener un númberu primu que nun ta nel conxuntu orixinal. Si, otra manera, ye compuestu, entós va esistir dalgún factor p qu'estreme a q. Suponiendo que p ye dalgunu de los pi, deduzse entós que p estrema a la diferencia , pero nengún númberu primu estrema a 1, esto ye, llegóse a un absurdu por suponer que p ta nel conxuntu orixinal. La consecuencia ye que'l conxuntu que s'escoyó nun ye refechu, yá que esisten númberos primos que nun pertenecen a él, y esto ye independiente del conxuntu finito que se tome.
Poro, el conxuntu de los númberos primos ye infinitu.
Si tómase como conxuntu'l de los n primeros númberos primos, entós , onde pn# ye lo que se llama primorial de pn. Un númberu primu de la forma pn# +1 denominar númberu primu d'Euclides n'honor al matemáticu griegu. Tamién puede ellaborase una demostración similar a la d'Euclides tomando'l productu d'un númberu dau de númberos primos menos unu, el llugar del productu d'esos númberos primos más unu. Nesi sentíu, denominar númberu primu primorial a un númberu primu de la forma pn# ± 1.
Non tolos númberos de la forma pn# +1 son primos. Nesti casu, como se sigue de la demostración anterior, tolos factores primos tendrán de ser mayores que n. Por casu: 2·3·5·7·11·13+1=30031=59·509
Otros matemáticos demostraron la infinitud de los númberos primos con diversos métodos procedentes d'árees de les matemátiques tales como al álxebra conmutativa y la topoloxía.[22] Dalgunes d'estes demostraciones basar nel usu de socesiones infinites cola propiedá de que cada unu de los sos términos ye coprimo con tolos demás, polo que se crea una biyección ente los términos de la socesión y un subconxuntu (infinitu) del conxuntu de los primos.
Una socesión que cumple dicha propiedá ye la socesión d'Euclides-Mullin, que deriva de la demostración euclídea de la infinitud de los númberos primos, yá que cada unu de los sos términos defínese como'l factor primu más pequeñu d'unu más el productu de tolos términos anteriores. La socesión de Sylvester definir de forma similar, yá que cada unu de los sos términos ye igual a unu más el productu de tolos anteriores. Anque los términos d'esta última socesión nun son necesariamente toos primos, cada unu d'ellos ye coprimo con tolos demás, polo que puede escoyese cualesquier de los sos factores primos, por casu, el menor d'ellos, y el conxuntu resultante va ser un conxuntu infinitu que los sos términos son toos primos.
Otros enunciaos qu'impliquen la infinitud de los númberos primos[editar | editar la fonte]
Una resultancia entá más fuerte, y qu'implica direutamente la infinitud de los númberos primos, foi afayáu por Euler nel sieglu XVIII. Establez que la serie ye diverxente. Unu de los teoremas de Mertens concreta más, estableciendo que :[23] onde la espresión O(1) indica qu'esi términu ta acutáu ente -C y C pa n mayor que n0, onde los valores de C y n0 nun tán especificaos.[24]
Otra resultancia ye'l teorema de Dirichlet, que diz asina:
|
El postuláu de Bertrand enuncia asina:
|
Una manera más débil pero elegante de formulalo ye que, si n ye un númberu natural mayor que 1, entós siempres esiste un númberu primu p tal que n < p < 2n. Esto supón que, nuna progresión xeométrica de primer términu enteru mayor que 3 y razón igual a 2, ente cada términu de la progresión y el siguiente, tiense siquier un númberu primu.
Frecuencia de los númberos primos[editar | editar la fonte]
10 4 −0,3 2,2 2,500 10² 25 3,3 5,1 4,000 10³ 168 23 10 5,952 10⁴ 1.229 143 17 8,137 10⁵ 9.592 906 38 10,425 10⁶ 78.498 6.116 130 12,740 10⁷ 664.579 44.158 339 15,047 10⁸ 5.761.455 332.774 754 17,357 10⁹ 50.847.534 2.592.592 1.701 19,667 1010 455.052.511 20.758.029 3.104 21,975 ... ... ... ... ...

Una vegada demostráu la infinitud de los númberos primos, cabo preguntar cómo se distribúin los primos ente los númberos naturales, esto ye, qué frecuentes son y ónde s'espera atopar el n-ésimo númberu primu. Esti estudiu empecipiar Gauss y Legendre de forma independiente a finales del sieglu XVIII, pal cual introducieron la función enumerativa de los númberos primos π(n), y conxeturaron que'l so valor fora aproximao :.[25]
L'enfotu de demostrar esta conxetura tomó tol sieglu XIX. Les primeres resultancies fueron llograos ente 1848 y 1859 por Chebyshov, quien demostró utilizando métodos puramente aritméticos la esistencia de dos constantes A y B tales que : pa n abondo grande. Consiguió demostrar que, si esistía la llende del cociente d'aquelles espresiones, este tenía de ser 1.
Hadamard y De la Vallée-Poussin ellaboraron una demostración en 1896, independientemente l'unu del otru, usando métodos similares, basaos nel usu de la función zeta de Riemann, que fuera introducida por Bernhard Riemann en 1859. Hubo qu'esperar hasta 1949 p'atopar una demostración qu'usara solu métodos elementales (esto ye, ensin usar el analís complexu). Esta demostración foi escurrida por Selberg y Erdős. Anguaño, conozse'l teorema como teorema de los númberos primos.
El mesmu Gauss introdució una estimación más precisa, utilizando la función llogaritmu integral:
- .
En 1899 De la Vallée-Poussin demostró que l'error que se comete averando d'esta forma ye : pa una constante positiva a y pa cada enteru m. Esta resultancia foi llixeramente ameyoráu a lo llargo de los años. Per otra parte, en 1901 Von Koch amosó que si la hipótesis de Riemann yera cierta, teníase la siguiente estimación, más precisa:[26]
Una forma equivalente al teorema de los númberos primos ye que pn, el n-ésimo númberu primu, queda bien averáu por nln(n). N'efeutu, pn ye puramente mayor qu'esti valor.
Diferencia ente dos primos consecutivos[editar | editar la fonte]
Amestáu a la distribución de los númberos primos atópase l'estudiu de los intervalos ente dos primos consecutivos. Esti intervalu, cola única salvedá del qu'hai ente'l 2 y el 3, ten de ser siempres igual o mayor que 2, yá que ente dos númberos primos consecutivos siquier hai un númberu par y por tanto compuestu. Si dos númberos primos tienen por diferencia 2, dizse que son ximielgos, y cola salvedá del "triplete" formáu polos númberos 3, 5 y 7, los númberos ximielgos preséntense siempres de dos en dos. Esto tamién ye bono de demostrar: ente tres números impares consecutivos mayores que 3 siempres hai unu que ye múltiplu de 3, y por tanto compuestu. Los primeros pares de númberos primos ximielgos son (3,5), (5,7), (11, 13), (17, 19) y (29, 31).
Per otra parte, la diferencia ente primos consecutivos pue ser tan grande como se quiera: dau un númberu natural n, se denota por n! el so factorial, esto ye, el productu de tolos númberos naturales entendíos ente 1 y n. Los númberos
son toos compuestos: si 2 ≤ i ≤ n+1, entós (n+1)!+i ye divisible ente i, por tanto, ye compuestu. La socesión, qu'entiende n enteros consecutivos, nun contién nengún númberu primu. Por casu, si n=5, estos valores correspuenden a:
El siguiente valor, 6!+7=727, ye primu.[27] De toes formes, el menor númberu primu que falta del siguiente en n ye xeneralmente enforma menor que'l factorial, por casu, el casu más pequeñu de dos primos consecutivos separaos d'ocho unidaes ye (89, 97), ente que 8! ye igual a 40.320.
La socesión de les diferencies ente primos consecutivos[28] foi profusamente estudiada en matemátiques, y alredor d'esti conceutu estableciéronse munches conxetures que permanecen ensin resolver.
Conclusión[editar | editar la fonte]


El modeláu de la distribución de los númberos primos ye una tema d'investigación recurrente ente los teóricos de númberos. La primalidá d'un númberu concretu ye (hasta agora) impredicible a pesar de qu'esisten lleis, como'l teorema de los númberos primos y el postuláu de Bertrand, que gobiernen la so distribución a gran escala. Leonhard Euler comentó:
Hasta'l día de güei, los matemáticos intentaron en devanéu atopar dalgún orde na socesión de los númberos primos, y tenemos motivos pa creer que ye un misteriu nel que la mente enxamás va enfusar.[29]
Nuna conferencia de 1975, Don Zagier comentó:
Hai dos fechos sobre la distribución de los númberos primos de los qu'espero convence-yos de forma tan incontestable que van quedar permanentemente grabaos nos sos corazones. El primeru ye que, a pesar de la so definición simple y del papel que desempeñen como lladriyos colos que se constrúin los númberos naturales, los númberos primos crecen como meruxes ente los númberos naturales, y nun paecen obedecer nenguna otra llei que la del azar, y naide puede predicir ónde va brotar el siguiente. El segundu fechu ye entá más estelante, yá que diz xustu lo contrario: que los númberos primos amuesen una regularidá ablucante, qu'hai lleis que gobiernen el so comportamientu, y qu'obedecen estes lleis con precisión casi militar.[30]
Atopar númberos primos[editar | editar la fonte]
Tests de primalidá[editar | editar la fonte]

La peñerada de Eratóstenes ye una manera senciella de topar tolos númberos primos menores o iguales qu'un númberu dau. Basar n'iguar una llista de tolos númberos naturales dende'l 2 hasta esi númberu y tachar repetidamente los múltiplos de los númberos primos yá descubiertos. La peñerada de Atkin, más moderna, tien una mayor complexidá, pero si optimízase apropiadamente tamién ye más rápida. Tamién esiste una recién peñerada de Sundaram que xenera namái númberos compuestos, siendo los primos los númberos faltantes.
Na práutica, lo que se desea ye determinar si un númberu dau ye primu ensin tener qu'iguar una llista de númberos primos. Un métodu pa determinar la primalidá d'un númberu ye la división per tentativa, que consiste n'estremar socesivamente esi númberu ente los númberos primos menores o iguales al so raigañu cuadráu. Si dalguna de les divisiones ye exacta, entós el númberu nun ye primu; en casu contrariu, ye primu. Por casu, dau n menor o igual que 120, pa determinar la so primalidá basta comprobar si ye divisible ente 2, 3, 5 y 7, una y bones el siguiente númberu primu, 11, yá ye mayor que √120. Ye'l test de primalidá más senciellu, y rápido pierde la so utilidá a la de comprobar la primalidá de númberos grandes, una y bones el númberu de factores posibles crez demasiáu rápido a midida que crez el númberu potencialmente primu.
N'efeutu, el númberu de númberos primos menores que n ye aproximao :. D'esta forma, pa determinar la primalidá de n, el mayor factor primu que se precisa nun ye mayor que √n, dexando'l númberu de candidatos a factor primu en cerca de :. Esta espresión crez cada vez más amodo en función de n, pero, como los n grandes son d'interés, el númberu de candidatos tamién se fai grande: por casu, pa n = 1020 tiénense 450 millones de candidatos.
Coles mesmes, esisten otros munchos tests de primalidá deterministes que se basen en propiedaes que caractericen a los númberos primos, pero la so utilidá computacional depende enforma del test usáu. Por casu, podría emplegase el teorema de Wilson pa calcular la primalidá d'un númberu, pero tien l'inconveniente de riquir el cálculu d'un factorial, una operación computacionalmente prohibitiva cuando se remanen númberos grandes. Equí ente en xuegu'l tiempu d'execución del algoritmu emplegáu, que s'espresa na notación de Landau. Pa poder determinar la primalidá de númberos cada vez más grandes (de miles de cifres) búsquense aquellos algoritmos que'l so tiempu d'execución creza lo más amodo posible, a ser posible, que pueda espresase como un polinomiu. Magar el test de primalidá AKS cumple con esta condición, pal rangu de númberos que s'usa na práutica esti algoritmu ye desaxeradamente lentu.
Per otra parte, de cutiu basta con tener una respuesta más rápida con una alta probabilidá (anque non segura) de ser cierta. Puede comprobase rápido la primalidá d'un númberu relativamente grande por aciu tests de primalidá probabilísticos. Estos tests suelen tomar un númberu aleatoriu llamáu «testigu» ya introducilu nuna fórmula xunto col númberu potencialmente primu n. Dempués de delles iteraciones, resuélvese que n ye «definitivamente compuestu» o bien «probablemente primu». Estos últimos númberos pueden ser primos o bien pseudoprimos (númberos compuestos que pasen el test de primalidá). Dalgunos d'estos tests nun son perfectos: puede haber númberos compuestos que'l test considere «probablemente primos» independientemente del testigu utilizáu. Esos númberos reciben el nome de pseudoprimos absolutos pa esi test. Por casu, los númberos de Carmichael son númberos compuestos, pero'l test de Fermat evaluar como probablemente primos. Sicasí, los tests probabilísticos más utilizaos, como'l test de Miller-Rabin o'l obsoleto test de Solovay-Strassen, superáu pol anterior, nun tienen esti inconveniente, entá siendo igualmente tests probabilísticos.
Dellos tests probabilísticos podríen pasar a ser determinísticos y dellos tests pueden ameyorar el so tiempu d'execución si verifíquense delles hipótesis matemátiques. Por casu, si verifícase la hipótesis xeneralizada de Riemann, puede emplegase una versión determinística del test de Miller-Rabin, y el test de primalidá por curves elíptiques podría ameyorar notablemente'l so tiempu d'execución si verificárense delles hipótesis de teoría analítica de númberos.
Algoritmos de factorización[editar | editar la fonte]
Un algoritmu de factorización ye un algoritmu que dixebra unu a unu los factores primos d'un númberu. Los algoritmos de factorización pueden funcionar tamién a manera de tests de primalidá, pero polo xeneral tienen un tiempu d'execución menos ventaxosu. Por casu, puede modificar l'algoritmu de división per tentativa de forma que nun se detenga cuando se llogre una división exacta, sinón que siga realizando nueves divisiones, y non sobre'l númberu orixinal, sinón sobre'l cociente llográu. Dempués de la división por tentativa, los métodos más antiguos que se conocen son el métodu de Fermat, que se basa nes diferencies ente cuadraos y que ye especialmente eficaz cuando n ye'l productu de dos númberos primos próximos ente sigo, y el métodu de Euler, que se basa na representación de n como suma de dos cuadraos de dos formes distintes.
Más apocayá, ellaboráronse algoritmos basaos nuna gran variedá de téuniques, como les fracciones continues o les curves elíptiques, anque dalgunos son meyores de métodos anteriores (la peñerada cuadrática, por casu, basar nuna meyora del métodu de Fermat y tien complexidá computacional subexponencial sobre'l númberu de cifres de n). Otros, como'l métodu rho de Pollard, son probabilísticos, y nun garanticen topar los divisores d'un númberu compuestu.
Lo que ye güei, l'algoritmu determinístico más rápidu d'usu xeneral ye'l xeneral number field sieve, que tamién tien complexidá computacional subexponencial sobre'l númberu de cifres de n.[31] Propúnxose un algoritmu que'l so tiempu d'execución ye polinómico sobre'l númberu de cifres de n (el algoritmu de Shor), pero rique ser executáu nun ordenador cuánticu, yá que'l so simulación nun ordenador normal rique un tiempu esponencial. Nun se conocen algoritmos pa factorizar nun ordenador tradicional en tiempu polinómico y tampoco se demostró qu'esto sía imposible.
Fórmules que solo xeneraren númberos primos[editar | editar la fonte]
A lo llargo de la historia, buscáronse numberoses fórmules pa xenerar los númberos primos. El nivel más altu d'esixencia pa una fórmula asina sería qu'acomuñara a cada númberu natural n el n-ésimo númberu primu. De forma más indulxente, puede pidise una función f inyectiva qu'acomuñe a cada númberu natural n un númberu primu de tala forma que cada unu de los valores tomaos apaeza solo una vegada.
Amás, esíxese que la función pueda aplicase, efectiva y conducentemente, na práutica.[32] Por casu, el teorema de Wilson asegura que p ye un númberu primu si y solu si (p-1)!≡-1 (mod p). Otru exemplu: la función f(n) = 2 + ( 2(n!) mod (n+1)) xenera tolos númberos primos, solo los númberos primos, y solo el valor 2 tómase más d'una vegada. Sicasí, dambes fórmules basar nel cálculu d'un factorial, lo que les fai computacionalmente invidables.
Na busca d'estes funciones, investigar, notablemente, les funciones polinómiques. Cabo sorrayar que nengún polinomiu, entá en delles variables, devuelve solu valores primos.[33] Por casu, el polinomiu nuna variable f(n) = n² + n + 41, estudiada por Leonardo Euler, devuelve valores primos pa n = 0,…, 39, sicasí pa n= 40, resulta un númberu compuestu.[34] Si'l términu constante val cero, entós el polinomiu ye múltiplu de n, polo que'l polinomiu ye compuestu pa valores compuestos de n. En casu contrariu, si c ye'l términu constante, entós f(cn) ye múltiplu de c, polo que si'l polinomiu nun ye constante, necesariamente tendrá d'incluyir valores compuestos.
Sicasí, hai polinomios en delles variables que los sos valores positivos (cuando les variables percuerren númberos naturales) son precisamente númberos primos. Un exemplu, ye esti polinomiu descubiertu por Jones, Sato, Wada y Wiens en 1976:[33]
Al igual qu'asocede coles fórmules con factoriales, esti polinomiu nun ye práuticu de calcular, yá que, anque los valores positivos que toma son toos primos, práuticamente nun devuelve otra cosa que valores negativos cuando se faen variar les variables a a z de 0 a infinitu.
Otru enfoque al problema d'atopar una función que solo xenere númberos primos vien dau a partir del teorema de Mills, qu'indica qu'esiste una constante θ tal que :
ye siempres un númberu primu, onde ye la función trío.[35] Inda nun se conoz nenguna fórmula pa calcular la constante de Mills, y los aproximamientos que s'empleguen na actualidá basar na socesión de los asina llamaos númberos primos de Mills (los númberos primos xeneraos por aciu esta fórmula), que nun pueden ser llograos rigorosamente, sinón solo de manera probabilística, suponiendo cierta la hipótesis de Riemann.
Clases de númberos primos[editar | editar la fonte]
De mayor interés son otres fórmules que, anque non solo xeneren númberos primos, son más rápides d'implementar, sobremanera si esiste un algoritmu especializáu que dexe calcular rápido la primalidá de los valores que van tomando. A partir d'estes fórmules llógrense subconxuntos relativamente pequeños del conxuntu de los númberos primos, que suelen recibir un nome coleutivu.
Primos primoriales y primos factoriales[editar | editar la fonte]
Los númberos primos primoriales, direutamente rellacionaos cola demostración euclidiana de la infinitud de los númberos primos, son los de la forma p = n# ± 1 pa dalgún númberu natural n, onde n# ye igual al productu 2 · 3 · 5 · 7 · 11 · … de tolos primos ≤ n. Coles mesmes, un númberu primu dizse primu factorial si ye de la forma n! ± 1. Los primeros primos factoriales son:
- n! − 1 ye primu pa n = 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, …[36]
- n! + 1 ye primu pa n = 0, 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, …[37]
Númberos primos de Fermat[editar | editar la fonte]

Los númberos de Fermat, amestaos a la construcción de polígonos regulares con regla y compás, son los númberos de la forma , con n natural. Los únicos númberos primos de Fermat que se conocen hasta la fecha son los cinco que yá conocía'l mesmu Fermat, correspondientes a n = 0, 1, 2, 3 y 4, ente que pa valores de n ente 5 y 32 estos númberos son compuestos.[38]
Pa determinar la so primalidá, esiste un test especializáu que'l so tiempu d'execución ye polinómico: el test de Pépin. Sicasí, los mesmos númberos de Fermat crecen tan rápido que solo se lo pudo aplicar pa valores de n pequeños. En 1999 aplicar pa n = 24. Pa determinar el calter d'otros númberos de Fermat mayores utilízase'l métodu de divisiones socesives y de esa manera a fecha de xunu de 2009 conócense 241 númberos de Fermat compuestos, anque na mayoría de los casos desconoza'l so factorización completa.[38]
Númberos primos de Mersenne[editar | editar la fonte]
Los númberos de Mersenne son los de forma Mp = 2p – 1, onde p ye primu.[39] Los mayores númberos primos conocíos son xeneralmente d'esta forma, yá que esiste un test de primalidá bien eficaz, el test de Lucas-Lehmer, pa determinar si un númberu de Mersenne ye primu o non.
Anguaño, el mayor númberu primu que se conoz ye M77 232 917 = 277 232 917 - 1, que tien 23 249 425 cifres nel sistema decimal. Trátase cronológicamente del 50ᵘ númberu primu de Mersenne conocíu y el so descubrimientu anunció'l 3 de xineru de 2018[40] gracies al proyeutu de computación distribuyida «Great Internet Mersenne Prime Search» (GIMPS).
Otres clases de númberos primos[editar | editar la fonte]
Esisten lliteralmente decenes de apellíos que pueden añader al conceutu de númberu primu pa referise a un subconxuntu que cumple dalguna propiedá concreta. Por casu, los númberos primos pitagóricos son los que pueden espresase na forma 4n+1. Dichu d'otra forma, tratar de los númberos primos que'l so restu al estremalos ente 4 ye 1. Otru exemplu ye'l de los númberos primos de Wieferich, que son aquellos númberos primos p tales que p2 estrema a 2p-1 - 1.
Dalgunes d'estes propiedaes referir a una rellación concreta con otru númberu primu:
- Númberos primos ximielgos: p y p+2 ser si son los dos primos.
- Númberu primu de Sophie Germain: dau p primu, ye de Sophie Germain si 2p + 1 tamién ye primu. Una socesión de númberos p1,p2,p3,··· ,pn toos ellos primos, tales que pi+1=2pi+1 pa tou i ∈ {1,2,···,n-1 }, denominar cadena (completa) de Cunningham de primera especie, y cumple por definición que cada unu de los términos, salvo'l postreru, ye un númberu primu de Sophie Germain. Créese que pa tou n natural esisten infinites cadenes de Cunningham de llargor n,[41] anque hasta la fecha naide apurrió prueba de que dicha afirmación sía cierta.
- Númberu primu de Wagstaff: p ser si , onde q ye otru númberu primu.[42][43]
Tamién se-yos da nomes especiales a delles clases de primos que dependen de la base de numberación emplegada o de la forma d'escribir los díxitos, y non d'una fórmula matemática. Ye'l casu de los númberos somirp (primos al aviesu), que son aquellos númberos primos tales que'l númberu llográu al invertir l'orde de les sos cifres tamién ye primu. Tamién ye'l casu de los númberos primos repunit, que son aquellos númberos primos que son concatenación d'unos. Si, en llugar de considerase'l sistema de numberación decimal considérase'l binariu, llógrase otru conxuntu distintu de númberos primos repunit que, amás, coincide col de los númberos primos de Mersenne. Finalmente, los númberos primos triádicos son aquellos númberos que son primos, capicúes y simétricos respectu d'una recta horizontal.
El que se-y dea un nome a una clase de númberos primos con una definición precisa nun significa que se conoza dalgún númberu primu que sía d'esa clase. Por casu, nun se conoz hasta'l momentu nengún númberu primu de Wall-Sun-Sun, pero la so relevancia anicia en qu'en 1992, antes de la demostración de Wiles del últimu teorema de Fermat, afayóse que la falsedá del teorema pa un númberu primu p dadu implicaba que p yera un númberu primu de Wall-Sun-Sun. Esto fizo que, mientres un tiempu, la busca de númberos primos d'esta clase fuera tamién la busca d'un contraejemplo del postreru teorema de Fermat.[44]
Conxetures[editar | editar la fonte]
Esisten numberoses entrugues abiertes alrodiu de los númberos primos. Munches d'elles son problemes bien antiguos, y una de les más significatives ye la hipótesis de Riemann, delles vegaes mentada nesti artículu como una conxetura que, de ser cierta, dexaría conocer numberoses resultancies relevantes en diversos campos de les matemátiques.
Hipótesis de Riemann[editar | editar la fonte]
Pa entender la hipótesis de Riemann, una conxetura enunciada en 1859 pero que, hasta la fecha (2024), sigue ensin resolvese, ye necesariu entender la función zeta de Riemann. Sía un númberu complexu con parte real mayor que 1. Entós,
La segunda igualdá ye una consecuencia del teorema fundamental de l'aritmética, y amuesa que la función zeta ta íntimamente rellacionada colos númberos primos.
Esisten dos tipos de ceros de la función zeta, esto ye, valores s pa los cualos ζ(s) = 0: los triviales, que son s=-2, s=-4, s=-6, etc. (los enteros pares negativos) y los non triviales, que son aquellos ceros que nun s'atopen na exa real. Lo qu'indica la hipótesis de Riemann ye que la parte real de tolos ceros non triviales ye igual a 1/2.
La veracidá de la hipótesis implica una fonda conexón colos númberos primos, n'esencia, nel casu de verificase, diz que los númberos primos tán distribuyíos de la forma más regular posible. Dende un puntu de vista físicu», diz grosso modo que les irregularidaes na distribución de los númberos primos solo vienen de ruiu aleatorio. Dende un puntu de vista matemáticu, diz que la distribución asintótica de los númberos primos (según el teorema de los númberos primos, la proporción de primos menores que n ye ) tamién ye cierta pa intervalos enforma menores, con un error d'aproximao'l raigañu cuadráu de n (pa intervalos próximos a n). Ta llargamente estendíu na comunidá matemática que la hipótesis sía cierta. En concretu, la presunción más simple ye que los númberos primos nun tendríen de tener irregularidaes significatives na so distribución ensin una bona razón.[45]
Otres conxetures[editar | editar la fonte]
Infinitud de ciertos tipos de númberos primos[editar | editar la fonte]
Munches conxetures traten sobre si hai infinitos númberos primos d'una determinada forma. Asina, conxetúrase qu'hai infinitos númberos primos de Fibonacci[46] ya infinitos primos de Mersenne, pero solo un númberu finito de primos de Fermat.[47] Nun se sabe si hai infinitos númberos primos d'Euclides.
Distribución de los númberos primos[editar | editar la fonte]
Tamién hai numberoses conxetures que s'ocupen de determinaes propiedaes de la distribución de los númberos primos. Asina, la conxetura de los númberos primos ximielgos enuncia qu'hai infinitos númberos primos ximielgos, que son pares de primos que la so estrema ye de 2. La conxetura de Polignac ye una versión más xeneral y más fuerte de l'anterior, yá que enuncia que, pa cada enteru positivu n, hai infinitos pares de primos consecutivos que difieren en 2n. De la mesma, una versión más débil de la conxetura de Polignac diz que tou númberu par ye la diferencia de dos númberos primos.
Coles mesmes, conxetúrase la infinidá de los primos de la forma n2 + 1. Según la conxetura de Brocard, ente los cuadraos de primos consecutivos mayores que 2 esisten siempres siquier cuatro números primos. La conxetura de Legendre establez que, pa cada n natural, esiste un númberu primu ente n2 y (n+1)2. Finalmente, la conxetura de Cramér, que la so veracidá implicaría la de Legendre, diz que:
Teoría aditiva de númberos[editar | editar la fonte]
Otres conxetures rellacionen delles propiedad aditivas de los númberos colos númberos primos. Asina, la conxetura de Goldbach diz que tou númberu par mayor que 2 puede escribise como suma de dos númberos primos, anque tamién esiste una versión más débil de la mesma conxetura según la cual tou númberu impar mayor que 5 puede escribise como suma de tres números primos. El matemáticu chinu Chen Jingrun demostró, en 1966, que n'efeutu, tou númberu par abondo grande puede espresase como suma de dos primos o como la suma d'un primu y de un númberu que ye'l productu de dos primos. ("semi-primu").[48]
Los cuatro problemes de Landau[editar | editar la fonte]
En 1912, Landau estableció nel Congresu Internacional de Matemáticos Quintu Congresu Internacional de Matemáticos de Cambridge una llista de cuatro de los problemes yá mentaos sobre númberos primos, que se conocen como los problemes de Landau. Nengún d'ellos ta resueltu hasta la fecha. Trátase de la conxetura de Goldbach, la de los númberos primos ximielgos, la de Legendre y la de los primos de la forma n2 + 1.[49]
Xeneralización del conceutu de númberu primu[editar | editar la fonte]
El conceutu de númberu primu ye tan importante que se vio xeneralizáu de delles maneres en diverses cañes de les matemátiques.
Elementos primos nun aniellu[editar | editar la fonte]

Pueden definise los elementos primos y los elementos irreducibles en cualesquier dominiu d'integridá.[50] En cualesquier dominiu de factorización única, como por casu, l'aniellu de los enteros, el conxuntu d'elementos primos equival al conxuntu de los elementos irreducibles, qu'en ye {…, −11, −7, −5, −3, −2, 2, 3, 5, 7, 11, …}.
Considérense por casu los enteros gaussianos , esto ye, los númberos complexos de la forma a+bi con a, b ∈ . Este ye un dominiu d'integridá, y los sos elementos primos son los primos gaussianos. Hai de solliñar que'l 2 non ye un primu gaussiano, porque almiti factorización como productu de los primos gaussianos (1+i) y (1-i). Sicasí, l'elementu 3 sí ye primu nos enteros gaussianos, pero nun lu ye n'otru dominiu enteru. Polo xeneral, los primos racionales (esto ye, los elementos primos del aniellu ) de la forma 4k+3 son primos gaussianos, pero nun lu son aquellos de la forma 4k+1.
Ideales primos[editar | editar la fonte]
En teoría d'aniellos, un ideal I ye un subconxuntu d'un aniellu A tal que * si i, j ∈ I, entós la suma i + j pertenez a I
- y si x ∈ A, i ∈ I, entós los productos a × i, i × a pertenecen a I.
Un ideal primu defínese entós como un ideal que cumple tamién que:
- pa cualquier par d'elementos a, b del aniellu A tales que'l so productu a × b pertenez a I, entós, siquier unu de los dos elementos, a o b, ta en I.
- I nun ye l'aniellu A enteru.
Los ideales primos son una ferramienta relevante en álxebra conmutativa, teoría alxebraica de númberos y xeometría alxebraica. Los ideales primos del aniellu d'enteros son los ideales (0), (2), (3), (5), (7), (11), …
Un problema central en teoría alxebraica de númberos ye la manera en que se factorizan los ideales primos cuando se ven sometíos a una estensión de cuerpos. Nel exemplu de los enteros gaussianos, (2) se ramifica en potencia d'un primu (yá que y xeneren el mesmu ideal primu), los ideales primos de la forma son inertes (caltienen la so primalidá) y los de la forma pasen a ser productu de dos ideales primos distintos.
Primos en teoría de la valoración[editar | editar la fonte]
En teoría alxebraica de númberos surde otra xeneralización más. Dau un cuerpu , reciben el nome de valoraciones sobre determinaes funciones de en . Caúna d'estes valoraciones xenera una topoloxía sobre , y dizse que dos valoraciones son equivalentes si xeneren la mesma topoloxía. Un primu de ye una clase d'equivalencia de valoraciones. Con esta definición, los primos del cuerpu de los númberos racionales queden representaos pola función valor absolutu según poles valoraciones p-ádicas sobre pa cada númberu primu p.
Nuedos primos[editar | editar la fonte]
 |
 |

| |
| Dellos nuedos primos. | |||
En teoría de nuedos, un nuedu primu ye un nuedu non trivial que nun se puede descomponer en dos nuedos más pequeños. De forma más precisa, tratar d'un nuedu que nun se puede escribir como suma conexa de dos nuedos non triviales.
En 1949 Horst Schubert demostró un teorema de factorización análogu al teorema fundamental de l'aritmética, qu'asegura que cada nuedu puede llograse de forma única como suma conexa de nuedos primos.[51] Por esti motivu, los nuedos primos desempeñen un papel central na teoría de nuedos: una clasificación de los nuedos foi dende finales del sieglu XIX la tema central de la teoría.
Aplicaciones na matemática[editar | editar la fonte]
- Nel estudiu de los númberos complexos, allegar al conceutu de «primos relativos» pa definir raigaños primitivos de la unidá .[52] Si n ye un númberu primu toes los raigaños enésimos de 1 son raigaños primitivos, salvo'l raigañu 1.
- Na definición d'un cuerpu finito, esíxese que'l númberu d'elementos d'un aniellu sía enteru primu. En tal casu, esaniciando'l cero, cada elementu tien inversu multiplicativu y llógrase la estructura d'un cuerpu.[53]
- Na definición d'un polígonu estrelláu de n llaos, pa tomar los puntos de m en m, esíxese que m sía menor que n/2 y primu con n.[54]
- Al definir el representante canónicu d'un númberu racional, usando clases d'equivalencia de pares ordenaos de númberos enteros, necesariamente, el par ordenáu definente tien qu'arreyar dos enteros primos relativos. A fortiori, a lo menos unu d'ellos, un primu absolutu.[55]
Aplicaciones na computación[editar | editar la fonte]
L'algoritmu RSA basar nel llogru de la clave pública por aciu la multiplicación de dos númberos grandes (mayores que 10100) que sían primos. La seguridá d'esti algoritmu anicia en que nun se conocen maneres rápides de factorizar un númberu grande nos sos factores primos utilizando ordenadores tradicionales.
Númberos primos nel arte y la lliteratura[editar | editar la fonte]
Los númberos primos influyeron en numberosos artistes y escritores. El compositor francés Olivier Messiaen valir d'ellos pa crear música non métrica. N'obres tales como La Nativité du Seigneur (1935) o Quatre études de rythme (1949-50) emplega simultáneamente motivos que la so duración ye un númberu primu pa crear ritmos impredicibles. Según Messiaen, esta forma de componer foi «inspirada polos movimientos de la naturaleza, movimientos de duraciones llibres y desiguales».[56]
Na so novela de ciencia ficción Contact, darréu afecha al cine, Carl Sagan suxure que los númberos primos podríen ser emplegaos pa comunicase con intelixencies estraterrestres, una idea que desenvolviera de manera informal col astrónomu estauxunidense Frank Drake en 1975.[57]
El curiosu incidente del perru a medianueche, de Mark Haddon, que describe en primer persona la vida d'un mozu autista bien dotáu en matemátiques y cálculu mental, utiliza namái los númberos primos pa numberar los capítulos.
Na novela PopCo de Scarlett Thomas, la güela de Alice Butler trabaya na demostración de la hipótesis de Riemann. El llibru ilustra una tabla de los mil primeros númberos primos.[58]
La solitudine dei numeri primi, novela escrita por Paolo Giordano, ganó'l premiu Strega en 2008.
Tamién son munches les películes que reflexen la fascinación popular escontra los misterios de los númberos primos y la criptografía, por casu, Cube, Sneakers, The Mirror Has Two Faces y A Beautiful Mind. Esta postrera basar na biografía del matemáticu y premiu Nobel John Forbes Nash, escrita por Sylvia Nasar.[59]
L'escritor griegu Apostolos Doxiadis, escribió El tíu Petros y la conxetura de Goldbach, que narra cómo un ficticiu matemática maravía de principios de sieglu XX somorguiar nel mundu de les matemátiques d'una forma apasionante. Tratando de resolver unu de los problemes más difíciles y entá non resueltos de la matemática «La Conxetura de Goldbach», la cual reza: «Tou númberu par puede espresase como la suma de dos númberos primos».
Ver tamién[editar | editar la fonte]
- Criptografía
- Espiral de Ulam
- Matemática
- Test de primalidá
- Númberos primos
- Tabla de factores primos
- Primu de Solinas
- Mayor númberu primu conocíu
Referencies[editar | editar la fonte]
- ↑ Niven y Zuckerman: Introducción a la teoría de númberos ISBN 968-18-069-7, páx. 19
- ↑ Burton W. Jones: Teoría de los númberos, Editorial Tríes. Méxicu D. F., páx.55
- ↑ Niven- Zuckerman. Introducción a la teoría de númberos
- ↑ Abramo Hefez: Cursu de álgebbra vol.1, ISBN 9972-9394-1-3, páx.87
- ↑ Marcus du Sautoy, La symphonie des nomes premiers P.42 (en francés)
- ↑ Préhistoire de la géométrie: le problème des sources, artículu d'Olivier Keller (en francés)
- ↑ «Nacencia de les matemátiques.». Consultáu'l 7 de xunu de 2009.
- ↑ Arnaldez, Roger y otros títulu=Les antigües ciencies del Oriente. (1988). . Barcelona: Ediciones Orbis S.A..
- ↑ Planetmath.org. «History of prime numbers.». Consultáu'l 7 de xunu de 2009.
- ↑ Crandall, Richard (2001). Prime numbers, a computational perspective. Nueva York: Springer-Verlag. ISBN 0-387-94777-9.
- ↑ Bernstein, Daniel. «Prime tests». Consultáu'l 1 de xunetu de 2009.
- ↑ Singh, Simon (1998). «Páx. 126», L'enigma de Fermat. Editorial Planeta S.A. ISBN 978-84-08-02375-3..
- ↑ Carles Pina i Estany. «Curiosidad sobre númberos primos.». Consultáu'l 5 de xunu de 2009.
- ↑ Hans Riesel, Prime Numbers and Computer Methods for Factorization. New York: Springer (1994): 36 (n'inglés)
- ↑ Richard K. Guy & John Horton Conway, The Book of Numbers. New York: Springer (1996): 129 - 130 (n'inglés)
- ↑ Gowers, T (2002). Mathematics: A Very Short Introduction. Oxford University Press, páx. 118. ISBN 0-19-285361-9. «La esclusión aparentemente arbitraria del 1 de la definición de númberu primu … nun espresa nenguna conocencia fonda sobre los númberos: trátase a cencielles d'un conveniu útil, adoptáu por que solo haya una manera de factorizar cualquier númberu nos sos factores primos»
- ↑ "Why is the number one not prime?" (n'inglés), aportáu'l 31-05-2009.
- ↑ "Arguments for and against the primality of 1" (n'inglés), aportáu'l 31-05-2009.
- ↑ Puede probase pol principiu d'inducción matemática
- ↑ Niven Zuckerman. Introducción a la teoría de númberos
- ↑ , Euclides (1991-1996). «Vol. II, llibru IX, proposición 20.», Elemento. Obra completa, Madrid, Editorial Gredos. ISBN 978-84-249-1463-9.
- ↑ DiAmOnD. «Demostración topolóxica de la infinitud de los númberos primos.». Consultáu'l 5 de xunu de 2009.
- ↑ Vease, por casu, An Introduction to the Theory of Numbers, p. 24. (n'inglés)
- ↑ Polo xeneral, na notación de Landau, indica que ta apoderada asintóticamente por , esto ye, . Pa más información, llea notación de Landau.
- ↑ Con esta espresión quier dicise que'l llende de la razón ente los dos espresiones tiende a 1 cuando n tiende a infinitu.
- ↑ von Koch, Helge. «Sur la distribution des nomes premiers». SpringerLink. Consultáu'l 6 de xunu de 2009.
- ↑ Nótese qu'esto nun tien por qué ser verdá polo xeneral, por casu, si n ye impar, tiense que n!+(n+1) ye divisible ente 2.
- ↑ (socesión A001223 n'OEIS)
- ↑ Julian Havil, Gamma: Exploring Euler's Constant (tapa dura). Princeton: Princeton University Press (2003): 163 (n'inglés)
- ↑ Julian Havil, Gamma: Exploring Euler's Constant (tapa dura). Princeton: Princeton University Press (2003): 171
- ↑ Eric W. Weisstein. «Number Field Sieve» (inglés). Consultáu'l 31 de mayu de 2009.
- ↑ Introducción del capítulu 3 del llibru de Ribenboim The new book of prime number records.
- ↑ 33,0 33,1 Prime Glossary - Matijasevic's Polynomial, aportáu'l 06-06-2009
- ↑ I.S. Sominski «Métodu d'inducción matemática» Editorial Mir, Moscú (1985) segunda edición
- ↑ W. H. Mills, A prime-representing function (1947) (n'inglés)
- ↑ (socesión A002982 n'OEIS)
- ↑ (socesión A002981 n'OEIS)
- ↑ 38,0 38,1 Keller, Wilfrid. «Fermat factoring status». Archiváu dende l'orixinal, el 10 de febreru de 2016. Consultáu'l 1 de xunu de 2009.
- ↑ DiAmOnD. «esponente compuestu-ye-tambien-compuestu/ Tou númberu de Mersenne con esponente compuestu ye tamién compuestu». Consultáu'l 7 de xunu de 2009. Por contraposición, deduzse que, pa buscar númberos primos de Mersenne, basta con buscar ente los númberos de Mersenne con esponente primu.
- ↑ «Mersenne Prime Discovery - 2^77232917-1 is Prime!» (inglés). Consultáu'l 2018-01-06.
- ↑ Nicholas Anderson, Andrew J. Havens, Brian Hydefrost, Sean Murphy y Steve Sarasin. «Prime Numbers and the Riemann Hypothesis» páxs. 6. Archiváu dende l'orixinal, el 15 de xunu de 2010. Consultáu'l 7 de xunu de 2009.
- ↑ The On-Line Encyclopedia of Integer Sequences!. «A000979. Wagstaff primes.». Archiváu dende l'orixinal, el 18 de xunu de 2010. Consultáu'l 23 d'abril de 2010.
- ↑ Weisstein, Eric W. «Wagstaff Prime» (inglés). MathWorld. Wolfram Research.
- ↑ Plantía:Prime Pages
- ↑ Bombieri, Enrico. «The Riemann hypothesis» (inglés). Clay Mathematics Institute. Archiváu dende l'orixinal, el 27 de marzu de 2009. Consultáu'l 6 de xunu de 2009.
- ↑ Plantía:Prime Pages
- ↑ Por casu, vease Unsolved Problems in Number Theory, Springer-Verlag, problema A3, páxs. 7–8.
- ↑ Tony Crilly (2011). 50 coses qu'hai que saber sobre matemátiques. Ed. Ariel. ISBN 978-987-1496-09-9.
- ↑ Mathworld - Landau's Problems (n'inglés)
- ↑ «Número alxebraicos». Archiváu dende l'orixinal, el 29 de mayu de 2009. Consultáu'l 7 de xunu de 2009.
- ↑ En Mathworld. (n'inglés)
- ↑ Kurosch. «Álxebra cimera»
- ↑ Fraleig. «Álxebra astracta»
- ↑ G.M.Cirgüeyu. «Elementos de xeometría»
- ↑ C. A. Trejo «El conceutu de númberu»
- ↑ Peter Hill (1994). Amadeus Press: The Messiaen companion..
- ↑ Carl Pomerance, Prime Numbers and the Search for Extraterrestrial Intelligence, aportáu'l 31-05-2009
- ↑ A Mathematician reviews PopCo (n'inglés), aportáu'l 31-05-2009
- ↑ Music of the Spheres, Seleición de Marcus du Sautoy de películes que traten sobre los númberos primos (n'inglés), aportáu'l 31-05-2009
Enllaces esternos[editar | editar la fonte]
- «peñerada-de-eratstenes-en-c Penera de Eratóstenes pa buscar los númberos primos aplicada en C/C++». Brainum Code. http://www.brainum.es/code/ccplusplus/sacando-nmeros-primos-pola peñerada-de-eratstenes-en-c.
- Calculador online de factores primos, por www.mathstools.com
- The Prime Pages
- Sobre l'artículu de Manindra Agrawal et al. PRIMES IS IN P, onde afirmen: "We present a deterministic polynomial-time algorithm that determines whether an input number n is prime or composite" mathmistakes
- Algoritmos eficientes pa calcular númberos primos, por Steve Litt
- ¿Ye esti númberu primu?
















![{\displaystyle \mathbb {Z} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d4da3ac703cc7721ebba91a53f6752de7157124)















































![{\displaystyle \mathbb {Z} [i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ffa94e9e2e6d9e5e5373d5fafb954b902743fde)









