Función matemática
| Función matemática | |
|---|---|
| conceutu matemáticu | |
|
rellación binaria, función parcial (es) | |
 | |

En matemátiques, dizse qu'una magnitú o cantidá ye función d'otru si'l valor de la primera depende del valor de la segunda. Por casu, l'área A d'un círculu ye función del so radiu r (el valor del área ye proporcional al cuadráu del radiu, A = π·r2). De la mesma, la duración T d'un viaxe en tren ente dos ciudaes separaes por una distancia d de 150 km depende de la velocidá v a la que se mueva'l tren (la duración ye inversamente proporcional a la velocidá, d / v). A la primer magnitú (l'área, la duración) #denominar variable dependiente, y la cantidá de la que depende (el radiu, la velocidá) ye la variable independiente.
N'analís matemáticu, el conceutu xeneral de función, aplicación o mapeo refierse a una regla qu'asigna a cada elementu d'un primer conxuntu un únicu elementu d'un segundu conxuntu (correspondencia matemática). Por casu, cada númberu enteru tien un únicu cuadráu, que resulta ser un númberu natural (incluyendo'l cero):
| ... | −2 → +4, | −1 → +1, | 0 → 0, |
| +1 → +1, | +2 → +4, | +3 → +9, | ... |
Esta asignación constitúi una función ente'l conxuntu de los númberos enteros Z y el conxuntu de los númberos naturales N. Anque les funciones que manipolien númberos son les más conocíes, nun son l'únicu exemplu: puede imaxinase una función qu'a cada pallabra del asturianu asígne-y la so lletra inicial:
| ..., | Estación → E, | Muséu → M, | Regueru → R, | Rosa → R, | Avión → A, | ... |
Esta ye una función ente'l conxuntu de les pallabres del Aasturianu y el conxuntu de les lletres del alfabetu asturianu.
La manera habitual de denotar una función f ye:
- f: A → B
- a → f(a),
onde A ye'l dominiu de la función f, el so primer conxuntu o conxuntu de partida; y B ye'l codominio de f, el so segundu conxuntu o conxuntu de llegada. Por f(a) se denota la regla o algoritmu pa llograr la imaxe d'un ciertu oxetu arbitrariu a del dominiu A, esto ye, el (únicu) oxetu de B que-y correspuende. N'ocasiones esta espresión ye abonda pa especificar la función por completu, infiriendo'l dominiu y codominio pol contestu. Nel exemplu anterior, les funciones cuadráu» y «inicial», llámese-yos f y g, se denotarían entós como:
- f: Z → N
- k → k2, o cenciellamente f(k) = k2;
- g: V → A
- p → Inicial de p;
si convien V = {Pallabres del asturianu} y A Alfabetu asturianu}.
Una función puede representase de diverses formes: por aciu el citáu algoritmu o ecuaciones pa llograr la imaxe de cada elementu, por aciu una tabla de valores qu'empareye cada valor de la variable independiente cola so imaxe —como les amosaes enriba—, o como una gráfica que dea una imaxe de la función.
Historia[editar | editar la fonte]

El conceutu de función como un oxetu matemáticu independiente, susceptible de ser estudiáu por sigo solo, nun apaeció hasta los entamos del cálculu nel sieglu XVII.[1] René Descartes, Isaac Newton y Gottfried Leibniz establecieron la idea de función como dependencia ente dos cantidaes variables. Leibniz en particular acuñó los términos «función», «variable», «constante» y «parámetru». La notación f(x) foi utilizada per primer vegada por A.C. Clairaut, y por Leonhard Euler na so obra Commentarii de San petersburgo en 1736.[2][3][4]
Primeramente, una función #identificar a efeutos práuticos con una espresión analítica que dexaba calcular los sos valores. Sicasí, esta definición tenía delles llimitaciones: espresiones distintes pueden refundiar los mesmos valores, y non toles dependencies» ente dos cantidaes pueden espresase d'esta manera. En 1837 Dirichlet propunxo la definición moderna de función numbérica como una correspondencia cualesquier ente dos conxuntos de númberos, qu'acomuña a cada númberu nel primer conxuntu un únicu númberu del segundu.
La intuición sobre'l conceutu de función tamién evolucionó. Primeramente la dependencia ente dos cantidaes imaxinábase como un procesu físicu, de cuenta que la so espresión alxebraica prindaba la llei física que correspondía a este. L'enclín a una mayor astracción viose reforzada a midida que atopáronse exemplos de funciones ensin espresión analítica o representación xeométrica sencielles, o ensin rellación con nengún fenómenu natural; y polos exemplos «patolóxicos» como funciones continues ensin derivada en nengún puntu.
Mientres el sieglu XIX Julius Wilhelm Richard Dedekind, Karl Weierstrass, Georg Cantor, partiendo d'un estudiu fondu de los númberos reales, desenvolvieron la teoría de funciones, siendo esta teoría independiente del sistema de numberación emplegáu.[cita [ensin referencies] Col desenvolvimientu de la teoría de conxuntos, nos sieglos XIX y XX surdió la definición actual de función, como una correspondencia ente dos conxuntos d'oxetos cualesquier, non necesariamente numbéricos.[5] Tamién se #acomuñar con otros conceutos venceyaos como'l de rellación binaria.
Introducción[editar | editar la fonte]

Una función ye un oxetu matemáticu que s'utiliza pa espresar la dependencia ente dos #magnitud, y puede presentase al traviés de dellos aspeutos complementarios. Un exemplu habitual de función numbérica ye la rellación ente la posición y el tiempu nel movimientu d'un cuerpu.
Un móvil que se mueve con una aceleración de 0,66 m/s2 percuerre una distancia d que ta en función del tiempu trescurríu t. Dizse que d ye la variable dependiente de t, la variable independiente. Estes magnitúes, calculaes a priori o midíes nun esperimentu, pueden conseñase de delles maneres. (Supónse que'l cuerpu parte nun intre nel que se convien que'l tiempu ye t = 0 s.)
Los valores de les variables pueden recoyese nuna tabla, anotando la distancia percorrida d nun ciertu intre t, pa dellos momentos distintos:
| Tiempu t (s) | Distancia d (m) |
|---|---|
| 0,0 | 0,0 |
| 0,5 | 0,1 |
| 1,0 | 0,3 |
| 1,5 | 0,7 |
| 2,0 | 1,3 |
| 2,5 | 2,0 |
La gráfica na imaxe ye una manera equivalente de presentar la mesma información. #Cada puntu de la curva colorada representa una pareya de #dato #tiempo-alloña, utilizando la correspondencia ente puntos y coordenaes del planu cartesianu. Tamién puede utilizase una regla o algoritmu que dicte como s'hai de calcular d a partir de t. Nesti casu, la distancia que percuerre un cuerpu con esta aceleración ta dada pola espresión:
- d = 0,33 × t2,
onde les magnitúes espresen unidaes del SI. D'estos trés maneres refléxase qu'esiste una dependencia ente dambes magnitúes.
Una función tamién puede reflexar la rellación d'una variable dependiente con delles variables independientes. Si'l cuerpu del exemplu #mover con una aceleración constante pero indeterminao a, la distancia percorrida ye una función entós d'a y t; en particular, d = a·t2/2. Les funciones tamién s'utilicen pa espresar la dependencia ente otros oxetos cualesquier, non solo los númberos. Por casu, esiste una función qu'a cada polígonu asígnalu los so númberu de llaos; o una función qu'a acaldía de la selmana asígna-y el siguiente:
- Llunes → Martes, Martes → Miércoles,..., Domingo → Llunes
Definición[editar | editar la fonte]
La definición xeneral de función fai referencia a la dependencia ente los elementos de dos conxuntos dados.
Un oxetu o valor xenéricu a nel dominiu A #denominar la variable independiente; y un oxetu xenéricu b del codominio B ye la variable dependiente. Tamién se-yos llama valores d'entrada y de salida, respeutivamente. Esta definición ye precisa, anque en matemátiques utiliza una definición formal más rigorosa, que constrúi les funciones como un oxetu concretu.
- Exemplos
- Tolos númberos reales tienen un cubu, polo qu'esiste la función «cubu» qu'a cada númberu nel dominiu R asígna-y los so cubu nel codominio R.
- Quitando al 0, tolos númberos reales tienen un únicu inversu. Esiste entós la función inversu» que'l so dominiu son los númberos reales non nulos R \ {0}, y con codominio R.
- #Cada mamíferu conocíu #clasificar nun xéneru, como Homo, Los sos o Loxodonta. Esiste por tanto una función «clasificación en xéneros» qu'asigna a cada mamíferu de la coleición M = {mamíferos conocíos} el so xéneru. El codominio de «clasificación en xéneros» ye la coleición G = {xéneros de Mammalia}.
- Esiste una función «área» qu'a cada triángulu del planu (na coleición T de toos ellos, el so dominiu), asígna-y los so área, un númberu real, depués el so codominio ye R.
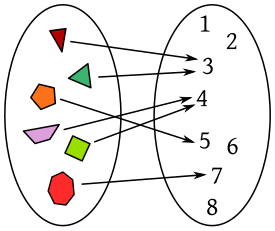
- Nunes eleiciones nes que cada votante pueda emitir un únicu votu, esiste una función «voto» qu'asigna a cada eleutor el partíu qu'escueya. Na imaxe amuésase un conxuntu d'eleutores Y y un conxuntu de partíos P, y una función ente ellos.
Funciones con múltiples variables[editar | editar la fonte]
Esisten munchos exemplos de funciones que «precisen dos valores» pa ser calculaes, como la función «tiempu de viaxe» T, que vien dada pol cociente ente la distancia d y la velocidá media v: cada pareya de númberos reales positivos (una distancia y una velocidá) tien acomuñada un númberu real positivu (el tiempu de viaxe). Poro, una función puede tener dos (o más) variables independientes.
La noción de función de múltiples variables independientes nun precisa d'una definición específica separada de la de función ordinaria». La xeneralidá de la definición anterior, na que se contempla que'l dominiu seya un conxuntu d'oxetos matemáticos arbitrarios, dexa omitir la especificación de dos (o más) conxuntos de variables independientes, A1 y A2, por casu. En llugar d'ello, el dominiu tómase como'l conxuntu de les pareyes (a1, a2), con primer componente n'A1 y segunda componente n'A2. Esti conxuntu #denominar el productu cartesianu d'A1 y A2, y se denota por A1 × A2.
D'esta miente los dos variables independientes queden axuntaes nun solu oxetu. Por casu, nel casu de la función T, el so dominiu ye'l conxuntu R+ × R+, el conxuntu de pareyes de númberos reales positivos. Nel casu de más de dos variables, la definición ye la mesma, usando un conxuntu ordenáu de múltiples oxetos, (a1,..., an), una n-tupla. Tamién el casu de múltiples variables dependientes #contemplar d'esta manera. Por casu, una función división puede tomar dos númberos naturales como valores d'entrada (dividendu y divisor) y refundiar dos númberos naturales como valores de salida (cociente y restu). Dizse entós qu'esta función tien como dominiu y codominio el conxuntu N × N.
Notación. Nomenclatura[editar | editar la fonte]
La notación habitual pa presentar una función f con dominiu A y codominio B ye:
Tamién se diz que f ye una función «d'A a B» o «ente A y B». El dominiu d'una función f se denota tamién por dom(f), D(f), Df, etc. Por f(a) #resumir la operación o regla que dexa llograr l'elementu de B acomuñáu a un ciertu a ∈ A, denomináu la imaxe d'a.
- Exemplos
- La función «cubu» puede denotarse agora como f: R → R, con f(x) = x3 pa cada númberu real x.
- La función inversu» ye g: R \ {0} → R, con g(x) = 1/x pa cada x real y non nulu.
- La función «clasificación en xéneros» puede escribise como γ: M → G, onde γ(m) = Xéneru de m, pa cada mamíferu conocíu m.
- La función «área» puédese denotar como A: T → R, y entós A(t) = Área de t = B · H/2, onde t ye un triángulu del planu, B la so base, y H el so altor.
- La función «voto» puede escribise como v: Y → P, onde v(a) = Partíu qu'a votó, pa cada votante a.
La notación utilizada pue ser un pocu más laxa, como por casu «la función f(n) = √n». En dicha espresión nun s'especifica que conxuntos se tomen como dominiu y codominio. Polo xeneral, estos van venir daos pol contestu nel que s'especifique dicha función. Nel casu de funciones de delles variables (dos, por casu), la imaxe del par (a1, a2) non se denota por f((a1, a2)), sinón por f(a1, a2), y similarmente para más variables.
Esisten amás terminoloxíes diverses en distintes cañes de les matemátiques pa referise a funciones con determinaos dominios y codominios:
- Función real: f: R → R
- Función complexa: f: C → C
- Función esguilar: f: Rn → R
- Función vectorial: f: Rn → Rm
Tamién les socesiones infinites d'elementos tales como a, b, c, ... son funciones, que'l so dominiu nesti casu son los númberos naturales. Les pallabres «función», «aplicación», «mapeo», o otres como «operador», «funcional», etc. pueden designar tipos concretos de función según el contestu. Adicionalmente, #dellos autores acuten la pallabra «función» pal casu nel que los elementos del conxuntu inicial y final son númberos.[6]
Imaxe ya imaxe inversa[editar | editar la fonte]

Los elementos del codominio B acomuñaos con dalgún elementu del dominiu A constitúin la imaxe de la función.
La xe d'un función
{} se denota por Im ( ) { {\tet{Im}}()} o
( A ) { f(A)} , ente que la imaxe d'un subconxuntu X
A {\textstyle X\subseteq A} se denota, de la mesma, por f ( X ) {\displaystyle f(X)} o f
X
{} . En notación conjuntista les imáxenes de f y X se denotan:

La imaxe d'una función f ye un subconxuntu del codominio de la mesma, pero nun son necesariamente iguales: pueden esistir elementos nel codominio que nun son la imaxe de nengún elementu del dominiu, esto ye, que nun tienen preimagen.
Asina, la preimagen d'un elementu del codominio puede nun contener nengún oxetu o, otra manera, contener unu o más oxetos, cuando a unu o dellos elementos del dominiu asígnase-yos dichu elementu del codominio. En notación conjuntista, escríbense:
- La imaxe de la función cubu f ye tou R, una y bones tou númberu real tien un raigañu cúbicu real. En particular, los raigaños cúbicos de los númberos positivos (negativos) son positives (negatives), polo que se tien, por casu, f−1(R+) = R+.
- El percorríu de la función inversu g nun ye igual a la so codominio, yá que nun hai nengún númberu real x que'l so inversu seya 0, 1/x = 0.
- Pa la función «clasificación en xéneros» γ tiense:
- γ(Perru) = Canis, y γ−1(Canis) = {Perru, coyote, chacal,...}.
- Como l'área ye siempres un númberu positivu, el percorríu de la función área A ye R+.
- Na diagrama puede comprobase que la imaxe de la función voto v nun coincide col codominio, una y bones el partíu C nun recibió nengún votu. Sicasí puede trate que, por casu, v−1(Partíu A) tien 2 elementos.
Igualdá de funciones[editar | editar la fonte]
Daes dos funciones, por que sían idéntiques han de tener el mesmu dominiu y codominio, y asignar la mesma imaxe a cada elementu del dominiu:
Funciones inyectivas, sobreyectivas y biyectivas[editar | editar la fonte]
La imaxe inversa d'un elementu del codominio puede ser vacida, o contener dellos oxetos del dominiu. Esto da llugar a la siguiente clasificación:
| Funciones | Inyectiva | Non inyectiva | ||
| Sobreyectiva |
|

| ||
| Non sobreyectiva | 
|

|
Les funciones inyectivas nun repiten les imáxenes: si b = f(a), nengún otru a' tien por imaxe a b, polo que la anti-imaxe d'esti postreru namái contién al elementu a. Les funciones suprayectivas percuerren tol codominio, polo que nenguna anti-imaxe puede tar vacida. La definición de función suprayectiva asume qu'esta tien un codominio especificáu primeramente. De lo contrario, la noción de suprayectividad nun tien sentíu.
Cuando una función tien dambes propiedaes al empar, dizse que ye una biyección ente dambos conxuntos:
Les funciones biyectivas constitúin un axugamientu perfectu» ente los elementos del dominiu y el codominio: cada elementu n'A tien una única «pareya» en B —como toles funciones—, y a cada elementu de B correspuénde-y unu solu n'A —siquier unu por ser suprayectiva, y como muncho unu por ser inyectiva—.
- Exemplos.
- La función cubu f: R → R ye biyectiva. Ye inyectiva porque dos númberos reales que tienen el mesmu cubu son idénticos, y ye suprayectiva porque Im(f) = R.
- La función inversu» g: R \ {0} → R ye inyectiva, una y bones l'inversu de cada númberu real non nulu ye únicu (1/x = 1/ya implica necesariamente que x = y). Sicasí nun ye suprayectiva, yá que Im(g) = R \ {0}.
- La función de clasificación de mamíferos γ: M → G nun ye inyectiva, yá que hai mamíferos distintos nel mesmu xéneru (por casu, γ(Yac) = γ(Toru) = Bos). Sicasí sí ye suprayectiva, yá qu'en cada xéneru de mamíferos hai clasificada siquier una especie de mamíferos.
- La función área A: T → R nun ye sobreyectiva, yá que Im(A) = R+. Tampoco ye inyectiva, yá que pueden construyise con #facilidad #triángulo distintos col mesmu área.
- Na imaxe pueden trate dellos exemplos de funciones ente un conxuntu de pinceles P y un conxuntu de cares C.
Álxebra de funciones[editar | editar la fonte]
Coles funciones puede realizase una operación de composición con propiedaes similares a les de la multiplicación.
Composición de funciones[editar | editar la fonte]

Daes dos funciones, so ciertes condiciones podemos usar los valores de salida d'una d'elles como valores d'entrada pa la otra., creando una nueva función.
Esto ye, la composición g ∘ f fai actuar primero la función f sobre un elementu d'A, y depués g sobre la imaxe que se llogre:
La condición Im(f) ⊆ C asegura precisamente qu'esti segundu pasu pueda llevase a cabu.
- Exemplos
- La imaxe de la función inversu» g ye R \ {0} —yá que tou númberu real non nulu ye l'inversu d'otru—, y por tanto ta conteníu nel dominiu de la función cubu f, que ye R. La composición f ∘ g: R \ {0} → R actúa entós como f(g(x)) = f(1/x) = (1/x)3 = 1/x3.
- Daes les funciones reales h1: R → R y h2: R → R daes por h1(x) = x2 y h2(x) = x + 1, puede tomase la composición en dambos órdenes, h1 ∘ h2 y h2 ∘ h1. Sicasí, son funciones distintes, yá que:
- (h1 ∘ h2)(x) = h1(h2(x)) = h1(x + 1) = (x + 1)2 = x2 + 2x + 1, y
- (h2 ∘ h1)(x) = h2(h1(x)) = h2(x2) = x2 + 1
- La función γ que clasifica los mamíferos en xéneros puede componese cola función ω: G → Or que clasifica los xéneros de mamíferos n'órdenes —que formen el conxuntu Or—. La función ω ∘ γ asigna a cada mamíferu'l so orde:
- (ω ∘ γ)(Humanu) = ω(Homo) = Primate, (ω ∘ γ)(Guanacu) = ω(Lama) = Artiodactyla
Función identidá[editar | editar la fonte]
En #cualquier conxuntu puede definise una función identidá, que teniendo como dominiu y codominio al propiu conxuntu, acomuña cada elementu consigo mesmu.
Tamién se denota como IA. La función identidá actúa como un elementu neutru al componer funciones, yá que nun fai nada». La función única sobre un conxuntu X qu'asigna cada elementu a sigo mesmu #denominar función d'identidá pa X y, típicamente, #indicar con idX. #Cada conxuntu tien la so propia función d'identidá, polo que'l subíndice nun puede omitise nun siendo que'l conxuntu pueda deducise del contestu. So composición, una función d'identidá ye "neutral": si f ye #cualquier función de X a Y, entós:
Función inversa[editar | editar la fonte]
Una función puede tener inversa, esto ye, otra función que al componela con ella resulte na identidá, de la mesma qu'un númberu multiplicáu pol so inversu da 1.
Non toles funciones son invertibles, sinón que solo aquelles que sían biyectivas tienen inversa:
La notación pa funciones inverses pue ser confusa. Pa un elementu del codominio b, f−1(b) puede denotar tantu la anti-imaxe de b (un subconxuntu del dominiu), como a la imaxe de b pola función inversa de f (un elementu del dominiu), nel casu de que f seya invertible.
- Exemplos.
- La función esponencial» h: R → R, qu'acomuña a cada númberu real el so esponencial, h(x) = ex, nun ye invertible, yá que nun ye suprayectiva: nengún númberu negativu pertenez a la imaxe de h.
- Esiste una función que calcula'l cambéu ente dos acolumbres. Nel casu del cambéu de rupies a quetzales (les monedes de la India y Guatemala), la conversión ta dada (en 2011) por: Q(r) = 0,15 × resta función de cambéu tien inversa, la conversión recíproca de quetzales a rupies: R(q) = 6,65 × q
- La función cubu f(x) = x3 ye invertible, yá que podemos definir la función inversa por aciu el raigañu cúbicu, f−1(x) = 3√x.
- La función de clasificación en xéneros γ: M → G nun ye invertible, yá que nun ye inyectiva, y pa cada xéneru pueden esistir dellos mamíferos clasificaos nél.
- La función qu'asigna a acaldía de la selmana'l so siguiente tien por inversa la función qu'asigna a acaldía de la selmana'l so antecesor:
- #Lunes → Domingo, Martes → Llunes,..., Domingo → Sábadu
Restricción y estensión[editar | editar la fonte]

La restricción d'una función dada ye otra función definida nuna parte del dominiu de la orixinal, pero que «actúa igual» qu'esta. Dizse tamién que la primera ye una estensión de la segunda. Informalmente, una restricción d'una función f ye la resultancia de retayar el so dominiu. De manera más precisa, si S ye un subconxuntu de X, la restricción de f a S ye la función f | S de S a Y tal que f | S (s) = f (s) pa tou s en S. Si g ye a Restricción de f, entós dizse que f ye una estensión de g.
La restricción d'una función f: A → B a un subconxuntu C ⊆ A se denota por f|C.
Representación de funciones[editar | editar la fonte]
Les funciones pueden presentase de distintes maneres:
- usando una rellación matemática descrita por aciu una espresión matemática: ecuaciones de la orma = f (
) {\displaystyle y=f(x)} . Cuando la rellación ye funcional, ye dicir satisfai la segunda condición de la definición de función, puede definise una función que se diz definida pola #rellación, Nun siendo que s'indique lo contrario, #suponer en tales casos que'l dominiu ye'l mayor posible (al respective de inclusión) y que'l codominio son tolos Reales. El dominiu escoyíu llámase'l dominiu natural, de la función.
- Exemplu: y=x+2. Dominiu natural ye tolos reales.
- Exemplu: "Pa tou x, númberu enteru, y vale x más dos unidaes".
- Como tabulación: tabla que dexa representar dellos valores discretos de la función.
- Exemplu:
- Como pares ordenaos: pares ordenaos, bien usaos en teoría de grafos.
- Exemplu: A={(-2, 0),(-1, 1),(0, 2),(1, 3),... (x, x+2)}
- Como gráfica: gráfica que dexa visualizar los enclinos na función. Bien utilizada pa les funciones continues típiques del cálculu, anque tamién les hai pa funciones discretes.
- Exemplu:
| 5 | X | |||||
| 4 | X | |||||
| 3 | X | |||||
| 2 | X | |||||
| 1 | X | |||||
| 0 | X | |||||
| y / x | -2 | -1 | 0 | 1 | 2 | 3 |
Espacios de función[editar | editar la fonte]
El conxuntu de toles funciones dende un conxuntu X a un conxuntu Y se denota X -> Y, por [X -> Y] o por X^Y. Esta postrera notación ta motivada pol fechu de que cuando X y Y son finitos y de tamañu |X| y |Y| entós el númberu de funciones de X -> Y ye |Y^X| = |Y|^|X| Este ye un exemplu de la convención de la combinatoria enumerativa qu'apurre anotaciones pa conxuntos basaos nos sos cardinalidades.Si X ye infinitu y hai más d'un elementu en Y entós hai innumberables funciones de X a Y, anque namái contablemente munches d'elles pueden espresase con una fórmula o un algoritmu.
Curtiendo (Currying)[editar | editar la fonte]
Un enfoque alternativu pa remanar funciones con múltiples argumentos ye tresformales nuna cadena de funciones que caúna toma un solu argumentu. Por casu, puede interpretase Add (3,5) pa significar "producir primero una función qu'añade 3 al so argumentu, y depués aplicar la función 'Sumar 3' a 5". Esta tresformamientu llámase "Currying": Add 3 ye curry (Add) aplicáu a 3. Hai una biyección ente los espacios de función CA × B y (CB) A.
Cuando se trabaya con funciones con curry, ye habitual usar la notación de prefixu cola aplicación de función considerada asociativa a la izquierda, una y bones la yuxtaposición de múltiples argumentos -como en (f x y) -de normal se correlaciona cola evaluación d'una función curry. Otra manera, los símbolos → y "are" considérense asociativos a la derecha, de cuenta que les funciones curry pueden definise por aciu una notación como f: ℤ → ℤ → ℤ = x ⟼ y ⟼ x · y.
Definición formal. Xeneralizaciones[editar | editar la fonte]
Les funciones pueden definise en términos d'otros oxetos matemáticos, como los conxuntos y los pares ordenaos. En particular, una función ye un casu particular de rellación binaria, depués esta definición ta basada na que s'adopte pa les rellaciones. Nel enfoque estensivu» identifícase una función cola so gráfica:
Na definición estensiva nun apaez el conceutu de codominio como conxuntu potencial onde ta conteníu'l percorríu. En delles árees de les matemátiques ye importante caltener esta distinción, y por tanto úsase una definición distinta:[7]
Con esta definición, dos funciones col mesmu grafo son distintes si'l so codominio nun coincide. Tamién se fala n'ocasiones de funciones parciales, pa les que non necesariamente cada elementu del dominiu tien una imaxe, en contraste coles funciones como se definieron antes, que se denominen totales. A les funciones parciales tamién-y les llama correspondencies o rellaciones unívoques.[8]
Ver tamién[editar | editar la fonte]
Referencies[editar | editar la fonte]
- ↑ Esta seición está basada en Pedro Ponte, J. (1992). «The history of the concept of function and some educational implications» (n'inglés). The Mathematics Educator 3 (2). http://math.coe.uga.edu/tme/issues/v03n2/Ponte.pdf. Consultáu'l 10 d'avientu de 2011.
- ↑ Dunham, William (1999). Euler: The Master of Us All. The Mathematical Association of America, páx. 17.
- ↑ Friedrich Gauss, Carl (1995). Academia Colombiana de Ciencias Exactas, Físicas y Naturales: .
- ↑ Howard Eves (1990). Foundations and Fundamental Concepts of Mathematics, 3, Dover, páx. 235. ISBN 0-486-69609-X.
- ↑ Dorronsoro, Jorge; Hernández, Eugenio (1996).
- ↑ Diccionario esencial de matemáticas.
- ↑ Al rodiu la diferencia ente dambes definiciones, vease por casu Forster, Thomas (2003). «§1.3.
- ↑ Gran enciclopedia temática Plaza.
Bibliografía[editar | editar la fonte]
- Dorronsoro, Jorge; Hernández, Eugenio (1996). Númberos, grupos y aniellos. Dorronsoro, Jorge; Hernández, Eugenio (1996). Números, grupos y anillos. Adison-Wesley Iberoamericana. ISBN 0-201-65395-8.


