Teoría de grafos

Teoría de grafos
	disciplina académica, especialidá, área de les matemátiques, especialidá y campu d'estudiu
	teoría y matemátiques

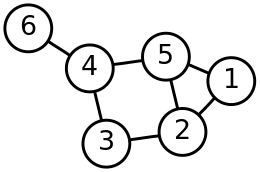Los grafos son l'oxetu d'estudiu d'esta caña de les matemátiques. Enriba'l grafo pez, en mediu'l grafo arcu y embaxo'l grafo dodecaedru.

La teoría de grafos, tamién llamada teoría de gráfiques, ye una caña de les matemátiques y les ciencies de la computación qu'estudia les propiedaes de los grafos, y que nun tienen de ser confundíos coles gráfiques que tienen una acepción bien amplia. Formalmente, un grafo $G=(V,Y)$ ye una pareya ordenada na que $V$ ye un conxuntu non vacíu de vértices y $Y$ ye un conxuntu d'arestes. Onde $V$ consta de pares ensin ordenar de vértices, tales como { ${x,y}$ } $\in Y$ entós dicimos que $x$ y $y$ son axacentes; y [nel grafo] representar por aciu una llinia ensin empobinar qu'una dichos vértices. Si'l grafo ye empobináu llámase-y digrafo, se denota $D$ , y entós el par $(x,y)$ ye un par ordenáu, y represéntase con una flecha que va de $x$ a $y$ , y dicimos que $(x,y)\in Y$ .^[1]

La teoría de grafos tien los sos fundamentos nes matemátiques discretes y de les matemátiques aplicaes. Esta teoría que rique de distintos conceutos de diverses árees como combinatoria, álxebra, probabilidá, xeometría de polígonos, aritmética y topoloxía. Anguaño tuvo mayor influencia nel campu de la informática, les ciencies de la computación y telecomunicaciones. Por cuenta de la gran cantidá d'aplicaciones na optimización de percorríos, procesos, fluxos, algoritmos de busques, ente otros, xeneróse toa una nueva teoría que se conoz como analís de redes.^[2]

Historia

L'orixe de la teoría de grafos remontar al sieglu XVIII col problema de les pontes de Königsberg, que consistía n'atopar un camín que percorriera los siete pontes del ríu Pregel (54°42′12″N 20°30′56″E / 54.70333°N 20.51556°E / 54.70333; 20.51556) na ciudá de Königsberg, anguaño Kaliningráu, de cuenta que se percorrieren toles pontes pasando una sola vegada per caúnu d'ellos. El trabayu de Leonhard Euler sobre'l problema tituláu Solutio problematis ad geometriam situs pertinentis^[3] (La solución d'un problema relativu a la xeometría de la posición) en 1736, ye consideráu la primer resultancia de la teoría de grafos. Tamién se considera unu de les primeres resultancies topolóxiques en xeometría (que nun depende de nenguna midida). Esti exemplu ilustra la fonda rellación ente la teoría de grafos y la topoloxía.

Depués, en 1847, Gustav Kirchhoff utilizó la teoría de grafos pal analís de redes llétriques publicando les sos lleis de los circuitos pa calcular el voltaxe y la corriente nos circuitos llétricos, conocíes como lleis de Kirchhoff, consideráu la primer aplicación de la teoría de grafos a un problema d'inxeniería.

En 1852 Francis Guthrie plantegó'l problema de los cuatro colores el cual afirma que ye posible, utilizando solamente cuatro colores, colorear cualquier mapa de países de tala forma que dos países vecinos nunca tengan el mesmu color. Esti problema, que nun foi resueltu hasta un sieglu dempués por Kenneth Appel y Wolfgang Haken en 1976, pue ser consideráu como la nacencia de la teoría de grafos. Al tratar de resolvelo, los matemáticos definieron términos y conceutos teóricos fundamentales de los grafos.

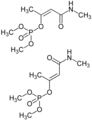
En 1857, Arthur Cayley estudió y resolvió el problema de enumeración de los isómeros, compuestos químicos con idéntica composición (fórmula) pero distintu estructura molecular. Pa ello representó cada compuestu, nesti casu hidrocarburos enchíos C_nH_2n+2, por aciu un grafo árbol onde los vértices representen átomos y les arestes la esistencia d'enllaces químicos.

El términu «grafo», provién de la espresión graphic notation («notación gráfica») usada per primer vegada por Edward Frankland^[4] y darréu adoptada por Alexander Crum Brown en 1884, y faía referencia a la representación gráfica de los enllaces ente los átomos d'una molécula.

El primer llibru sobre teoría de grafos foi escritu por Dénes Kőnig y publicáu en 1936.^[5]

Composición d'un grafo

Arestes: Son les llinies coles que se xunen los vértices d'un grafo.
- Arestes axacentes: 2 arestes son axacentes si converxen nel mesmu vértiz.
- Arestes paraleles: Son dos arista conxuntes si'l vértiz inicial y final son el mesmu.
- Aresta cícliques: Ye l'aresta que parte d'un vértiz pa entrar en sí mesmu.
- Encruz: Son 2 arestes que crucien nun mesmu puntu.

Vértices: Los vértices son los elementos que formen un grafo. Cada unu lleva acomuñada una valencia carauterística según la situación, que se correspuende cola cantidá d'arestes que conflúin en dichu vértiz.

Camín: Denominar camín d'un grafo a un conxuntu de vértices interconectaos por arestes. Dos vértices tán coneutaos si hai un camín ente ellos.

Tipos de grafos

Grafo simple: O a cencielles grafo ye aquel qu'acepta una sola aresta xuniendo dos vértices cualesquier. Esto ye equivalente a dicir qu'una aresta cualesquier ye la única que xune dos vértices específicos. Ye la definición estándar d'un grafo.
Multigrafo: Ye'l qu'acepta más d'una aresta ente dos vértices. Estes arestes llámense múltiples o llazos (loops n'inglés). Los grafos simples son una subclase d'esta categoría de grafos. Tamién se-yos llama grafos xeneral.
Pseudografo: Si inclúi dalgún llazu.
Grafo empobináu: grafo empobináu o digrafo. Son grafos nos cualos añadióse una orientación a les arestes, representada gráficamente por una flecha.
Grafo etiquetáu: Grafos nos cualos añadióse un pesu a les arestes (númberu enteru xeneralmente) o un etiquetáu a los vértices.
Grafo aleatoriu: Grafo que les sos arestes tán acomuñaes a una probabilidá.
Hipergrafo: Grafos nos cualos les arestes tienen más de dos estremos, esto ye, les arestes son incidentes a 3 o más vértices.
Grafo infinitu: Grafos con conxuntu de vértices y arestes de cardinal infinitu.
Grafo planu: Los grafos planos son aquellos que los sos vértices y arestes pueden ser representaos ensin nenguna interseición ente ellos. Podemos establecer qu'un grafo ye planu gracies al Teorema de Kuratowski.
Grafo regular: Un grafo ye regular cuando tolos sos vértices tienen el mesmu grau de valencia.

Representación de grafos

Esisten distintes formes de representar un grafo (simple), amás de la xeométrica y munchos métodos p'almacenalos nun ordenador. La estructura de datos usada depende de les carauterístiques del grafo y el algoritmu usáu pa manipolialo. Ente les estructures más sencielles y usaes atópense les llistes y les matrices, anque frecuentemente úsase una combinación de dambes. Les llistes son preferíes en grafos esvalixaos porque tienen un eficiente usu de la memoria. Per otru llau, les matrices aproven accesu rápidu, pero pueden consumir grandes cantidaes de memoria.

Estructura de llista

Llista d'incidencia - Les arestes son representaes con un vector de pares (ordenaos, si'l grafo ye empobináu), onde cada par representa una de les arestes.^[6]

Llista d'axacencia - Cada vértiz tien una llista de vértices los cualos son axacentes a él. Esto causa redundancia nun grafo non empobináu (yá que A esiste na llista d'axacencia de B y viceversa), pero les busques son más rápides, al costu d'almacenamientu extra.

Secuencia de graos Llista de graos - Tamién llamada secuencia de graos o socesión gráfica d'un grafo non-empobináu ye una secuencia de númberos, que correspuende a los graos de los vértices del grafo.

Estructures matriciales

Matriz d'axacencia - El grafo ta representáu por una matriz cuadrada M de tamañu $n^{2}$ , onde $n$ ye'l númberu de vértices. Si hai una aresta ente un vértiz x y un vértiz y, entós l'elementu $m_{x,y}$ ye 1, de lo contrario, ye 0.

Matriz d'incidencia - El grafo ta representáu por una matriz d'A (arestes) por V (vértices), onde [vértiz, aresta] contién la información de l'aresta (1 - conectáu, 0 - non conectáu)

Grafo G(V,A)	Conxuntos	Matriz d'axacencia	Matriz d'incidencia	Secuencia de graos	Llista d'Axacencia
	V = { 1, 2, 3, 4, 5, 6 } A = { {1,1}, {1,2}, {1,5}, {2,3}, {2,5}, {3,4}, {4,5}, {4,6} }	${\begin{pmatrix}1&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\\\end{pmatrix}}$	${\begin{pmatrix}1&1&1&0&0&0&0&0\\0&1&0&1&1&0&0&0\\0&0&0&1&0&1&0&0\\0&0&0&0&0&1&1&1\\0&0&1&0&1&0&1&0\\0&0&0&0&0&0&0&1\\\end{pmatrix}}$	(3,3,2,3,3,1)	{ {1,2,5}, {1,3,5}, {2,4}, {3,5,6},{1,2,4},{4} }

Problemes de teoría de grafos

Subgrafos, subgrafos inducíos y menores

Un problema común, denomináu problema d'isomorfismu de subgrafos, ye atopar un grafo fixu como subgrafo d'un grafo dau. Una razón pa tar interesáu nesta cuestión ye que munches propiedaes de grafos son heredaes de subgrafos, lo que significa qu'un grafo tien una propiedá si y solu si tolos sos subgrafos de la mesma tener. Desafortunadamente, atopar subgrafos máximos d'un ciertu tipu suel ser un problema NP-completu. Por casu:

Atopar el subgrafo completu más grande llámase problema de la clique.

Un problema similar ye atopar subgrafo inducíu nun grafo dau. De nuevu, delles propiedaes importantes son heredaes con al respective de subgrafos inducíos, lo que significa qu'un grafo tien una propiedá si y solu si tolos subgrafos inducíos tener. Atopar subgrafos inducíos máximos d'un determináu tipu ye, de nuevu, un problema NP-completu. Como exemplu:

Atopar el subgrafo inducíu más grande ensin cantos o conxuntu independiente denominar problema del conxuntu independiente.

Otru nuevu problema ye'l problema del menor conteníu, que ye atopar un grafo fixu como menor d'un grafo dau. Un menor o subcontración d'un grafo ye cualesquier grafo llográu tomando un subgrafo y contrayendo dellos cantos. Munches propiedaes de grafos son heredaes de menores, lo que significa qu'un grafo tener namái si tolos sos menores tener tamién. Por casu, el teorema de Wagner axusta que:

Un grafo ye planu si contién como menor nin el grafo bipartitu completu nin el grafo completu.

Un problema de les mesmes carauterístiques ye'l problema de la subdivisión del conteníu. Una subdivisión o homeomorfismo d'un grafo ye cualesquier grafo llográu subdividiendo dellos cantos. La subdivisión del conteníu ta rellacionada coles propiedaes de los grafos tales como la "planeza". Por casu, el teorema de Kuratowski establez que:

Un grafo ye planu si contién una subdivisión nin el grafo bipartitu nin el grafo completu.

Otru problema na subdivisión de conteníu ye la conxetura de Kelmans-Seymour:

Cada grafo de cinco vértice coneutaos que nun ye planu contién una subdivisión del grafo completu de cinco vértice.

Otru problemes de clases tienen que ver col algame pa la cual delles especies y xeneralizaciones de grafos tán determinaes poles sos subgrafos de puntos esaniciaos. Por casu, la conxetura de la reconstrucción.

Ciclos y caminos hamiltonianos

Un ciclu ye una socesión d'arestes axacentes, onde nun se percuerre dos veces la mesma aresta, y onde se torna al puntu inicial. Un ciclu hamiltoniano tien amás que percorrer tolos vértices esautamente una vegada (sacante'l vértiz del que parte y al cual llega).

Por casu, nun muséu grande (al estilu del Louvre), lo aparente sería percorrer toles sales una sola vegada, esto ye buscar un ciclu hamiltoniano nel grafo que representa'l muséu (los vértices son les sales, y les arestes los corredores o puertes ente elles).

Fálase tamién de Camín hamiltoniano si nun s'impon tornar al puntu de partida, como nun muséu con una única puerta d'entrada. Por casu, un caballu puede percorrer tolos caxellos d'un tableru d'axedrez ensin pasar dos veces pola mesma: ye un camín hamiltoniano. Exemplu d'un ciclu hamiltoniano nel grafo del dodecaedru.

Anguaño, nun se conocen métodos xenerales pa topar un ciclu hamiltoniano en tiempu polinómico, siendo la busca por fuercia bruto de tolos posibles caminos o otros métodos descomanadamente costosos. Esisten, sicasí, métodos pa refugar la esistencia de ciclos o caminos hamiltonianos en grafos pequeños.

El problema de determinar la esistencia de ciclos hamiltonianos, entra nel conxuntu de los NP-completus.

Grafos planos

Cuando un grafo o multigrafo puede dibuxase nun planu ensin que dos segmentos se corten, dizse que ye planu.

Un xuegu bien conocíu ye'l siguiente: Dibúxense trés cases y tres pozos. Tolos vecinos de les cases tienen el derechu d'utilizar los trés pozos. Como nun se lleven bien n'absolutu, nun quieren cruciase enxamás. ¿Ye posible trazar los nueve caminos que xunten los trés cases colos trés pozos ensin qu'haya cruces?

Cualquier disposición de les cases, los pozos y los caminos implica la presencia de siquier un encruz.

Sía K_n el grafo completu con n vértices, K_{n, p} ye'l grafo bipartitu de n y p vértices.

El xuegu anterior equival a afayar si'l grafo bipartitu completu K_3,3 ye planu, esto ye, si puede dibuxase nun planu ensin qu'haya cruces, siendo la respuesta que non. Polo xeneral, puede determinase qu'un grafo non ye planu, si nel so diseñu puede atopara una estructura análoga (conocida como menor) a K₅ o a K_3,3.

Establecer qué grafos son planos nun ye obviu, y ye un problema que tien que ver con topoloxía.

Coloración de grafos

Si G=(V, Y) ye un grafo non empobináu, una coloración propia de G, asocede cuando coloreamos los vértices de G de cuenta que si {a, b} ye una aresta en G entós a y b tienen distintos colores. (Poro, los vértices axacentes tienen colores distintos). El númberu mínimu de colores necesarios pa una coloración propia de G ye'l númberu cromáticu de G y escríbese como C (G). Sía G un grafo non empobináu sía λ el númberu de colores disponibles pa la coloración propia de los vértices de G. El nuesu oxetivu ye atopar una función polinomial P (G,λ), na variable λ, llamada <o>polinomiu cromáticu de G</o>, que nos indique'l númberu de coloraciones mesmes distintes de los vértices de G, usando un máximu de λ colores.

Descomposición de polinomios cromáticos. Si G=(V, Y) ye un grafo conexu y y pertenez a Ε, entós: P (G,λ)=P (G+y,λ)+P (G/y,λ), onde G/y ye el grafo llograr por contraición d'arestes.

Pa cualesquier grafo G, el términu constante en P (G,λ) ye 0

Sía G=(V, Y) con |Y|>0 entós, la suma de los coeficientes de P (G,λ) ye 0.

Sía G=(V, Y), con a, b pertenecientes al conxuntu de vértices V pero {a, b}=y, non perteneciente a al conxuntu d'arestes Y. Escribimos G+y pal grafo que se llogra de G al añader l'aresta y={a, b}. Al identificar los vértices a y b en G, llogramos el subgrafo G++y de G.0000

Teorema de los cuatro colores

Mapa coloriáu con 4-colores.

Grafo dual acomuñáu al mapa con una 4-vértice coloración.

Otru problema famosu relativu a los grafos: ¿Cuántos colores son necesarios pa dibuxar un mapa políticu, cola condición obvia que dos países axacentes nun puedan tener el mesmu color? Supónse que los países son d'un solu cachu, y que'l mundu ye esféricu o planu. Nun mundu en forma de toroide; el teorema siguiente nun ye válidu:

Cuatro colores son siempres abondos pa colorear un mapa.

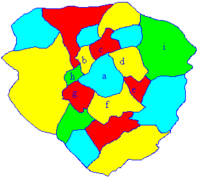
El mapa siguiente amuesa que trés colores nun basten: Si empezar pol país central a y esfórciase unu n'utilizar el menor númberu de colores, entós na corona alredor de a alternen dos colores. Llegando al país h tiense qu'introducir un cuartu color. Lo mesmo asocede en i si emplega'l mesmu métodu.

La forma precisa de cada país nun importa; lo único relevante ye saber qué país toca a qué otru. Estos datos tán incluyíos nel grafo onde los vértices son los países y les arestes conecten los que xustamente son axacentes. Entós la cuestión equival a atribuyir a cada vértiz un color distintu del de los sos vecinos.

Vimos que trés colores nun son abondos, y demostrar que con cinco siempres se llega, ye abondo fácil. Pero'l teorema de los cuatro colores nun ye nada obviu. Prueba d'ello ye que se tuvieron qu'emplegar ordenadores p'acabar la demostración (fíxose un programa que dexó verificar un ensame de casos, lo qu'aforró bien de tiempu a los matemáticos). Foi la primer vegada que la comunidá matemática aceptó una demostración asistida por ordenador, lo que creó nel so día una ciertu discutiniu dientro de dicha comunidá.

Carauterización de grafos

Grafo simple

Un grafo ye simple si a lo sumo esiste una aresta xuniendo dos vértices cualesquier. Esto ye equivalente a dicir qu'una aresta cualesquier ye la única que xune dos vértices específicos.

Un grafo que nun ye simple denominar multigrafo.

Grafos conexos

Un grafo ye conexu si cada par de vértices ta conectáu per un camín; esto ye, si pa cualquier par de vértices (a, b), esiste siquier un camín posible dende a escontra b.

Un grafo ye doblemente conexu si cada par de vértices ta conectáu por siquier dos caminos dixuntos; esto ye, ye conexu y nun esiste un vértiz tal que al sacalo'l grafo resultante sía disconexo.

Ye posible determinar si un grafo ye conexu usando un algoritmu Busca n'anchor (BFS) o Busca en fondura (DFS).

En términos matemáticos la propiedá d'un grafo (fuertemente) conexu dexa establecer una rellación d'equivalencia pa los sos vértices, que lleva a una partición d'estos en "componentes (fuertemente) conexos", esto ye, porciones del grafo, que son (fuertemente) conexes cuando se consideren como grafos aisllaos. Esta propiedá ye importante pa munches demostraciones en teoría de grafos.

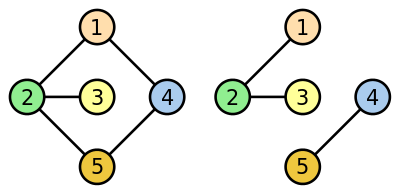
Grafos completos

Un grafo ye completu si esisten arestes xuniendo tolos pares posibles de vértices. Esto ye, tou par de vértices (a, b) tien de tener una aresta y que los xune.

El conxuntu de los grafos completos ye denomináu usualmente $\mathbb {K}$ , siendo $\mathbb {K} _{n}$ el grafo completu de n vértices.

Un $\mathbb {K} _{n}$ , esto ye, grafo completu de $n$ vértices tien esautamente ${\frac {n(n-1)}{2}}$ arestes.

La representación gráfica de los $\mathbb {K} _{n}$ como los vértices d'un polígonu regular da cuenta de la so peculiar estructura.

Grafos bipartitos

Un grafo G ye bipartitu si puede espresar como $G=\{V_{1}\cup V_{2},A\}$ (esto ye, los sos vértices son la unión de dos grupos de vértices), so les siguientes condiciones:

$V_{1}$ y $V_{2}$ son dixuntos y non vacíos.
Cada aresta d'A xune un vértiz de V₁ con unu de V₂.
Nun esisten arestes xuniendo dos elementos de V₁; análogamente pa V₂.

So estes condiciones, el grafo considérase bipartitu, y puede describise informalmente como'l grafo que xune o rellaciona dos conxuntos d'elementos distintos, como aquellos resultantes de los exercicios y puzzles nos que tien de xunise un elementu de la columna A con un elementu de la columna B.

Homeomorfismo de grafos

Dos grafos $G_{1}$ y $G_{2}$ son homeomorfos si dambos pueden llograse a partir del mesmu grafo con una socesión de subdivisiones elementales d'arestes.

Árboles

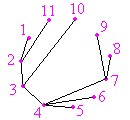
Un grafo que nun tien ciclos y que coneuta a tolos puntos, llámase un árbol. Nun grafo con n vértices, los árboles tienen esautamente n - 1 arestes, y hai n^n-2 árboles posibles. La so importancia anicia en que los árboles son grafos que conecten tolos vértices utilizando'l menor númberu posible d'arestes. Un importante campu d'aplicación del so estudiu atopar nel analís filoxenéticu, el de la filiación d'entidaes que deriven unes d'otres nun procesu evolutivu, que s'aplica sobremanera a l'averiguación del parentescu ente especies; anque s'usó tamién, por casu, nel estudiu del parentescu ente llingües.

Grafos ponderaos o etiquetaos

En munchos casos, ye precisu atribuyir a cada aresta un númberu específicu, llamáu valuación, ponderación o costu según el contestu, y llógrase asina un grafo valuáu.
Formalmente, ye un grafo con una función v: A → R₊.

Por casu, un representante comercial tien que visitar n ciudaes coneutaes ente sigo per carreteres; el so interés previsible va ser embrivir la distancia percorrida (o'l tiempu, si pueden prevese atascos). El grafo correspondiente va tener como vértices les ciudaes, como arestes les carreteres y la valuación va ser la distancia ente elles.
Y, pel momento, nun se conocen métodos xenerales pa topar un ciclu de valuación mínima, pero sí pa los caminos dende a hasta b, ensin más condición.

Diámetru

Nun grafo, la distancia ente dos vértices ye'l menor númberu d'arestes d'un percorríu ente ellos. El diámetru, nuna figura como nun grafo, ye la mayor distancia d'ente tolos pares de puntos de la mesma.

El diámetru de los K_n ye 1, y el de los K_n,_p ye 2. Un diámetru infinitu puede significar que'l grafo tien una infinidá de vértices o a cencielles que nun ye conexu. Tamién puede considerase el diámetru permediu, como'l permediu de les distancies ente dos vértices.

Una aplicación d'esti conceutu ye la hipótesis conocida como los seis graos de separación, que plantega que, si cada unu de los habitantes de la Tierra representar por un vértiz y dos persones tán coneutaes por una aresta si conócense personalmente, la distancia ente dos persones escoyíes al azar ente tolos habitantes de la Tierra ye de seis arista o menos.

El mundu d'Internet punxo de moda esa idea del diámetru: Si refugamos los sitios que nun tienen enllaces, y escoyemos dos páxina web al azar: ¿En cuántos clics puede pasase de la primera a la segunda? La resultancia ye'l diámetru de la Rede, vista como un grafo que los sos vértices son los sitios, y que les sos arestes son lóxicamente los enllaces.

Esti conceutu reflexa meyor la complexidá d'una rede que'l númberu de los sos elementos.

Aplicaciones

Gracies a la teoría de grafos pueden resolvese diversos problemes como por casu la síntesis de circuitos secuenciales, contadores o sistemes d'apertura. Utilizar pa distintes árees por casu, Dibuxu computacional, en toa les árees d'Inxeniería.

Los grafos utilícense tamién pa modelar trayectos como'l d'una llinia d'autobús al traviés de les cais d'una ciudá, nel que podemos llograr caminos óptimos pal trayeutu aplicando diversos algoritmos como pue ser l'algoritmu de Floyd.

Pa l'alministración de proyeutos, utilizamos téuniques como téunica de revisión y evaluación de programes (PERT) nes que se modelen los mesmos utilizando grafos y optimizando los tiempos pa concretar los mesmos.

Una importante aplicación de la teoría de grafos ye nel campu de la informática, yá que sirvió pal resolución d'importantes y complexos algoritmos. Un claru exemplu ye l'Algoritmu de Dijkstra, utilizáu pa la determinación del camín más curtiu nel percorríu d'un grafo con determinaos pesos nos sos vértices.

Dientro d'esti campu, un grafo ye consideráu un tipu de datu astractu TAD.

El científicu d'Estaos Xuníos Donald Knuth estableció los grafos planos como base de determinaos estudios y descubrimientos realizaos por él.

Per otra parte, destaca'l Algoritmu de Kruskal, que déxanos buscar un subconxuntu d'arestes qu'inclúi tolos vértices, estableciendo a lo menos el valor de les arestes.

La teoría de grafos tamién sirvió d'inspiración pa les ciencies sociales, cuantimás pa desenvolver un conceutu non metafóricu de rede social que sustitúi los nodos polos actores sociales y verifica la posición, centralidad ya importancia de cada actor dientro de la rede. Esta midida dexa cuantificar y abstraer rellaciones complexes, de manera que la estructura social puede representase gráficamente. Por casu, una rede social puede representar la estructura de poder dientro d'una sociedá al identificar los venceyos (arestes), la so direición ya intensidá y da idea de la manera en que'l poder tresmítese y a quién.

Emplegar en problemes de control de producción, pa proyeutar redes d'ordenadores, pa diseñar módulos electrónicos modernos y proyeutar sistemes físicos con parámetros alcontraos (mecánicos, acústicos y llétricos).

Usar pa la solución de problemes de xenética y problemes d'automatización de la proyeición (SAPR). Sofitu matemáticu de los sistemes modernos pal procesamientu de la información. Allega nes investigaciones nucleares (téunica de diagrames de Feynman).^[7]

Los grafos son importantes nel estudiu de la bioloxía y hábitat. El vértiz representa un hábitat y les arestes (o "edges" n'inglés) representa los senderos de los animales o les migraciones. Con esta información, los científicos pueden entender cómo esto puede camudar o afectar a les especies nel so hábitat.

Mapes conceptuales
Planu d'estaciones del metro.
Planu d'autopistes.
Circuitu llétricu
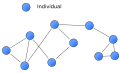
Sociograma d'una rede social
Topoloxía de rede d'ordenadores Ficheru:Ministry
Organigrames
Isomeros
Arquiteutura de redes de telefonía móvil
Draws d'eliminación direuta (ej: tenis)

Ente les aplicaciones de la Teoría de gráfiques que se volvieron importantes na actualidá podemos atopar l'estudiu de les redes sociales, que la so importancia anicia nel fayadizu almacenamientu de datos, yá que el costu del tiempu de busca de la información de cada miembru que pertenez a esta rede puede tornase demasiáu altu debíu al númberu d'usuarios. Por casu, el númberu d'usuarios qu'hai anguaño nuna importante rede social tan solo en Méxicu ye de 49 millones -cifra reportada pol periódicu L'economista en 2014-, si esti númberu multiplicar por 194 que ye'l númberu averáu de países qu'hai nel mundu, percíbese la posibilidá d'un grave problema d'almacenamientu pa los servidores qu'hai destinaos pa ello y pa la busca d'información. Este mesmu fenómenu pasa n'otres redes de fotografíes, mensaxes, etc. El modeláu d'esti tipu de problemes foi encetáu principalmente por estudiantes de doctoráu d'universidaes como Stanford, Massachusetts Institute of Technology (MIT), Berkeley, Oxford, Rice y tamién pola NASA; en Méxicu, tantu l'Institutu Politéunicu Nacional (IPN) como la Universidá Nacional Autónoma de Méxicu (UNAM) son los principales promotores nestes árees al traviés de los grupos académicos de combinatoria y de computación científica. Podemos considerar qu'esti tipu de problemes son trataos por espertos en matemátiques y ciencies de la computación, por cuenta del so altu grau de complexidá.

El celebru humanu ye una rede complexa que interactúa en rexones coneutaes por tractos de sustancia blanco. La carauterización de carauterístiques estructurales y funcionales d'una rede tal en suxetos sanos y persones enfermes tien la posibilidá d'ameyorar la nuesa comprensión de la fisiopatoloxía y les manifestaciones neurolóxiques y condiciones psiquiátriques. Esto llevó al usu de nueves ferramientes pal analís de sistemes complexos pa faer frente enfermedaes cerebrales. Ente estos, la teoría de grafos ye un marcu matemáticu que dexa describir una rede en forma d'una gráfica, que consiste nuna coleición de los nodos (esto ye, rexones del celebru) y los cantos (esto ye, estructurales y conexones funcionales) .L'usu de la teoría de grafos, distintu cambeos de la topoloxía de red cerebro fueron identificaos mientres el desenvolvimientu y l'avieyamientu normal, y rompiéronse conectividades funcionales y estructurales fueron acomuñáu con dellos trestornos neurolóxicu y psiquiátricu, incluyendo llocura, esclerosis llateral amiotrófica, y l'esquizofrenia. Nesti últimu enfoque contribuyóse a probar la teoría d'esta condición como un síndrome de desconexón. Na esclerosis múltiple (MS), l'escurrimientu de la desconexón foi acotada por estudios de resonancia magnética estructural de topoloxía de la rede cerebral qu'amosó un amenorgamientu de la conectividad estructural de les rexones de los lóbulos fronto-temporal.

Otra aplicación de les gráfiques consiste en tomar datos de resonancia magnética del celebru adquiríos en condición ausente ( estáu de reposu ) riquen nuevos analises de datos téuniques que nun dependen d'un modelu d'activación, una alternativa son los métodos llibre de parámetru sobre la base d'una forma particular de la centralidad del vector propiu asociáu a un nodo llamáu de centralidad; la centralidad del vector propiu asigna atributos d'un valor a cada voxel nel celebru de manera que un voxel recibe un valor grande si ta fuertemente correlacionada con munchos otros nodos que son centrales dientro de la rede; l'algoritmu PageRank de Google ye una variante del vector propiu centralidad el cual ye utilizáu nes busques que s'efectúen n'internet. Hasta'l momentu, otres midíes de centralidad - en particular centralidad d'intermediación - aplicáronse a datos de la fMRI usando un conxuntu pre-escoyíu de nodos que consisten en dellos cientos d'elementos. Centralidad del Vector Propiu ye computacionalmente muncho más eficiente que centralidad d'intermediación y nun riquir d'estragales de valores de semeyanza de cuenta que puede aplicase a miles de voxels nuna rexón d'interés que cubren la totalidá del celebru que sería invidable l'usu de centralidad d'intermediación. Centralidad del Vector Propiu puede utilizase nuna variedá de distintes midíes de semeyanza. (Lohmann et al., 2010). “La teoría de redes complexes xuega un papel importante nuna amplia variedá de disciplines, que van dende la informática, socioloxía, inxeniería y física, pa molecular y la bioloxía de la población. Dientro de los campos de la bioloxía y la medicina, el potencial d'aplicaciones d'analises de redes inclúin, por casu, la identificación oxetivu de drogues, determinando una función del xen de la proteína, o diseñar estratexes eficaces pal tratamientu de diverses enfermedaes o apurrir el diagnósticu precoz de trestornos. “ (Pavlopoulos et al., 2011) La teoría de gráfiques, ye afecha por que los informáticos modelen problemes, pero tamién ye afechu pa los matemáticos que tienen interés na complexidá computacional. La mayoría de los conceutos clásicos de la teoría de grafos teórica y aplicada (árboles d'espansión, conectividad, xéneru, colorabilidad, flúi nes redes, los apareyamientos y percorríos). Usar na solución de problemes.(Czumaj, Jansen, Meyer auf der Heide, & Schiermeyer, 2006)

Algoritmos importantes

Investigadores relevantes en teoría de grafos

Ver tamién

Referencies

↑ (2001). Algebraic Graph Theory. New York: Springer.
↑ CEPAL Charles Sobre Sistemes Complexos Sociales (CCSSCS): Analisis de Redes1: https://www.youtube.com/watch?v=oy8YxTshZhI&list=UUQbp2yá-gyew7Y_tzgOI36A & Analisis de Redes2: https://www.youtube.com/watch?v=1abtP36Wx24&list=UUQbp2yá-gyew7Y_tzgOI36A; Cursu completu en llinia: http://www.martinhilbert.net/CCSSCS.html
↑ Euler, L. (1736). «Solutio problematis ad geometriam situs pertinentis». Commentarii Academiae Scientiarum Imperialis Petropolitanae 8. 128-140. http://math.dartmouth.edu/~euler/docs/originals/Y053.pdf.
↑ http://booklens.com/l-r-foulds/graph-theory-applications páx.7
↑ Tutte, W.T., Graph Theory, Cambridge University Press, p. 30, ISBN 978-0-521-79489-3, https://books.google.com/books?id=uTGhooU37h4C&pg=PA30 .
↑ Exemplu d'una llista d'incidencia
↑ Gorbátov:«Fundamentos de la matemática discreta»

Czumaj, A., Jansen, K., Meyer auf der Heide, F., & Schiermeyer, I. (2006). Algorithmic Graph Theory. Oberwolfach Reports, 379–460.

Hinz, A. M. (2012). Graph theory of tower tasks. In Behavioural Neurology (Vol. 25, páxs. 13–22).

Lohmann, G., Margulies, D. S., Horstmann, A., Pleger, B., Lepsien, J., Goldhahn, D., … Turner, R. (2010). Eigenvector centrality mapping for analyzing connectivity patterns in fMRI data of the human brain. PLoS ONE, 5(4). http://doi.org/10.1371/journal.pon.0010232

Pavlopoulos, G. a, Secrier, M., Moschopoulos, C. N., Soldatos, T. G., Kossida, S., Aerts, J., … Bagos, P. G. (2011). Using graph theory to analyze biological networks. BioData Mining, 4(1), 10. Retrieved from http://www.biodatamining.org/content/4/1/10

Rocca, M. A., Valsasina, P., Meani, A., Falini, A., Comi, G., & Filippi, M. (2014). Impaired functional integration in multiple sclerosis: a graph theory study. Brain Structure and Function, 115–131. http://doi.org/10.1007/s00429-014-0896-4

Enllaces esternos

Sobre los grafos VPT y los grafos EPT. Mazzoleni, María Pía. 30 de mayu de 2014.
El conteníu d'esti artículu incorpora material d'una entrada de la Enciclopedia Libre Universal, espublizada en castellán baxo la llicencia Creative Commons Compartir-Igual 3.0.

Kaufmann, Walter Arnold

[1] (2001). Algebraic Graph Theory. New York: Springer.

[2] CEPAL Charles Sobre Sistemes Complexos Sociales (CCSSCS): Analisis de Redes1: https://www.youtube.com/watch?v=oy8YxTshZhI&list=UUQbp2yá-gyew7Y_tzgOI36A & Analisis de Redes2: https://www.youtube.com/watch?v=1abtP36Wx24&list=UUQbp2yá-gyew7Y_tzgOI36A; Cursu completu en llinia: http://www.martinhilbert.net/CCSSCS.html

[3] Euler, L. (1736). «Solutio problematis ad geometriam situs pertinentis». Commentarii Academiae Scientiarum Imperialis Petropolitanae 8. 128-140. http://math.dartmouth.edu/~euler/docs/originals/Y053.pdf.

[4] ttp://booklens.com/l-r-foulds/graph-theory-applications páx.7

[5] Tutte, W.T., Graph Theory, Cambridge University Press, p. 30, ISBN 978-0-521-79489-3, https://books.google.com/books?id=uTGhooU37h4C&pg=PA30 .

[6] Exemplu d'una llista d'incidencia

[7] Gorbátov:«Fundamentos de la matemática discreta»

[1]

[2]

[3]

[4]

[5]

[6]

[7]