Lleis de Kirchhoff

Les lleis de Kirchhoff son dos igualdaes que se basen na caltenimientu de la enerxía y la carga nos circuitos llétricos. Fueron descrites per primer vegada en 1846 por Gustav Kirchhoff. Son llargamente usaes n'inxeniería llétrica y inxeniería electrónica.

Dambes lleis de circuitos pueden derivase direutamente de les ecuaciones de Maxwell, pero Kirchhoff precedió a Maxwell y gracies a Georg Ohm el so trabayu foi xeneralizáu. Estes lleis son utilizaes pa topar corrientes y tensiones en cualquier puntu d'un circuitu llétricu.

Llei de corrientes de Kirchhoff[editar | editar la fonte]

La corriente que pasa por un nodo ye igual a la corriente que sale del mesmu. *i₁ + i₄ = i₂ + i₃*

Esta llei tamién ye llamada llei de nodos o primer llei de Kirchhoff y ye común que s'use la sigla LCK pa referise a esta llei. La llei de corrientes de Kirchhoff diznos que:

{{teorema|En cualesquier nodo, la suma de les corrientes qu'entren nesi nodo ye igual a la suma de les corrientes que salen. De forma equivalente, la suma de toles corrientes que pasen pol nodo ye igual a cero

\sum _{k=1}^{n}I_{k}=I_{1}+I_{2}+I_{3}+\dots +I_{n}=0

|-} Esta fórmula ye válida tamién pa circuitos complexos:

\sum _{k=1}^{n}{\tilde {I}}_{k}=0

La llei basar nel principiu de la caltenimientu de la carga onde la carga en coulombios ye'l productu de la corriente n'amperios y el tiempu en segundos.

Por definición, un nodo ye un puntu d'una rede llétrica nel cual converxen trés o más conductores.

Esta primer llei confirma'l principiu del caltenimientu de les cargues llétriques.

Densidá de carga variante[editar | editar la fonte]

La LCK solo ye válida si la densidá de carga caltiénse constante nel puntu nel que s'aplica. Considere la corriente entrando nuna llámina d'un condensador. Si unu imaxínase una superficie zarrada alredor d'esa llámina, la corriente entra al traviés del dispositivu, pero nun sale, violando la LCK. Amás, la corriente al traviés d'una superficie zarrada alredor de tol capacitor va cumplir la LCK entrante por una llámina sía banciada pola corriente que sale de la otra llámina, que ye lo que se fai n'analís de circuitos, anque cabo resaltar qu'hai un problema al considerar una sola llámina. Otru exemplu bien común ye la corriente nes antenes , onde la corriente entra del alimentador del tresmisor pero nun hai corriente que sala del otru llau sinón que los electrones salen proyeutaos/tremaos armónicamente escontra l'atmósfera circundante.

Maxwell introdució'l conceutu de corriente de desplazamientu pa describir estes situaciones. La corriente que flúi na llámina d'un capacitor ye igual al aumentu de l'acumuladura de la carga y amás ye igual a la tasa de cambéu del fluxu llétrico por cuenta de la carga (el fluxu llétrico tamién se mide en Coulombs, como una carga llétrica nel SIU). Esta tasa de cambéu del fluxu $\psi \$ , ye lo que Maxwell llamó corriente de desplazamientu $I_{\mathrm {D} }$ :

I_{\mathrm {D} }={\frac {d\psi }{dt}}

Cuando la corriente de desplazamientu inclúyese, la llei de Kirchhoff cumplir de nuevu. Les corrientes de desplazamientu nun son corrientes reales por cuenta de que nun consten de cargues en movimientu, deberíen trate más como un factor de correición pa faer que la LCK cumplir. Nel casu de la llámina del capacitor, la corriente entrante de la llámina ye atayada por una corriente de desplazamientu que sale de la llámina y entra pola otra llámina.

Esto tamién puede espresase en términos del vector campu al tomar la Llei de Ampere de la diverxencia cola correición de Maxwell y combinando la llei de Gauss, llogrando:

\nabla \cdot \mathbf {J} =-\nabla \cdot {\frac {\partial \mathbf {D} }{\partial t}}=-{\frac {\partial \rho }{\partial t}}

Esto ye a cencielles la ecuación del caltenimientu de la carga en forma integral, diz que la corriente que flúi al traviés d'una superficie zarrada ye igual a la tasa de perda de carga del volume zarráu (Teorema de Diverxencia). La llei de Kirchhoff ye equivalente a dicir que la diverxencia de la corriente ye cero, pa un tiempu invariante p, o siempres verdad si la corriente de desplazamientu ta incluyida en J.

Llei de tensiones de Kirchhoff[editar | editar la fonte]

Esta llei ye llamada tamién segunda llei de Kirchhoff, llei de llazos de Kirchhoff o llei de mallas de Kirchhoff (ye común que s'use la sigla LVK pa referise a esta llei).

Nun llazu zarráu, la suma de toles cayíes de tensión ye igual a la tensión total suministrada. De forma equivalente, la suma alxebraica de les diferencies de potencial llétricu nun llazu ye igual a cero.
$\sum _{k=1}^{n}V_{k}=V_{1}+V_{2}+V_{3}\dots +V_{n}=0$

D'igual manera que cola corriente, les tensiones tamién pueden ser complexos, asina:

\sum _{k=1}^{n}{\tilde {V}}_{k}=0

Esta llei basar nel caltenimientu d'un campu potencial d'enerxía. Dau una diferencia de potencial, una carga que completó un llazu zarráu nun gana o pierde enerxía al tornar al potencial inicial.

Esta llei ye cierta inclusive cuando hai resistencia nel circuitu. La validez d'esta llei puede esplicase al considerar qu'una carga nun torna al so puntu de partida, por cuenta de la disipación d'enerxía. Una carga a cencielles va terminar nel terminal negativu, en vegada del positivu. Esto significa que tola enerxía dada pola diferencia de potencial foi dafechu consumida pola resistencia, que va tresformar en calor. Teóricamente, y, yá que les tensiones tienen un signu, esto traduzse con un signu positivu al percorrer un circuitu dende un mayor potencial a otru menor, y al aviesu: con un signu negativu al percorrer un circuitu dende un menor potencial a otru mayor.

En resume, la llei de tensión de Kirchhoff nun tien nada que ver cola ganancia o perda d'enerxía de los componentes electrónicos (Resistores, capacitores, etc.). Ye una llei que ta rellacionada col campu potencial xeneráu por fontes de tensión. Nesti campu potencial, ensin importar que componentes electrónicos tean presentes, la ganancia o perda de la enerxía dada pel campu potencial ten de ser cero cuando una carga completa un llazu.

Campu llétrico y potencial llétricu[editar | editar la fonte]

La llei de tensión de Kirchhoff puede trate como una consecuencia del principiu del caltenimientu de la enerxía. Considerando esi potencial llétricu defínese como una integral de llinia, sobre un campu llétrico, la llei de tensión de Kirchhoff puede espresase como:

\oint _{C}\mathbf {Y} \cdot d\mathbf {l} =0,

Que diz que la integral de llinia del campu llétrico alredor d'un llazu zarráu ye cero.

Pa tornar a una forma más especial, esta integral puede "partise" pa consiguir la tensión d'un componente n'específicu.

Casu práuticu[editar | editar la fonte]

Asumiendo una rede llétrica consistente en dos fuentes y tres resistencies, disponemos el siguiente resolución: (antes d'empezar, ye necesariu esclariar la convención de signos: si percuerro la malla a favor de la corriente, el potencial acomuñáu a la resistencia ye negativu; casu contrariu ye positivu. Si percuerro la fonte y hai una xubida de potencial (de - a +), la fem ye positiva; casu contrariu ye negativa).

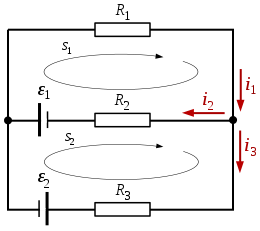
Acordies cola primer llei de Kirchhoff (llei de los nodos), tenemos:

i_{1}-i_{2}-i_{3}=0\,

La segunda llei de Kirchhoff (llei de les mallas), aplicada a la malla según el circuitu zarráu s₁, fainos llograr:

-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}=0

La segunda llei de Kirchhoff (llei de les mallas), aplicada a la malla según el circuitu zarráu s₂, pela so parte:

-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}=0

Por cuenta de lo anterior, plantégasenos un sistema d'ecuaciones coles incógnites $i_{1},i_{2},i_{3}$ :

{\begin{cases}i_{1}-i_{2}-i_{3}&=0\\-R_{2}i_{2}+\epsilon _{1}-R_{1}i_{1}&=0\\-R_{3}i_{3}-\epsilon _{2}-\epsilon _{1}+R_{2}i_{2}&=0\\\end{cases}}

Daes les magnitúes:

R_{1}=100,\ R_{2}=200,\ R_{3}=300,\ \epsilon _{1}=3,\ \epsilon _{2}=4

, la solución

definitiva sería:

{\begin{cases}i_{1}={\frac {1}{1100}}\\i_{2}={\frac {4}{275}}\\i_{3}=-{\frac {3}{220}}\\\end{cases}}

Puede reparase que $i_{3}$ tien signu negativu, lo cual significa que la direición de $i_{3}$ ye inversa respectu de lo qu'asumimos nun principiu (la direición de $i_{3}$ -en colloráu definida na imaxe).