Coordenaes polares

Les coordenaes polares o sistema de coordenaes polares son un sistema de coordenaes bidimensional nel que cada puntu del planu determinar por una distancia y un ángulu. Esti sistema ye llargamente utilizáu en física y trigonometría.

De manera más precisa, como sistema de referencia tómase: (a) un puntu O del planu, al que se llama orixe o polu; y (b) una recta empobinada (o rayu, o segmentu OL) que pasa por O, llamada exa polar (equivalente a la exa x del sistema cartesianu). Con esti sistema de referencia y una unidá de midida métrica (pa poder asignar distancies ente cada par de puntos del planu), tou puntu P del planu correspuende a un par ordenáu (r, θ) onde r ye la distancia de P al orixe y θ ye l'ángulu formáu ente la exa polar y la recta empobinada OP que va de O a P. El valor θ crez en sentíu antihorario y escai en sentíu horariu. La distancia r (r ≥ 0) conozse como la coordenada radial» o «radiu vector», ente que l'ángulu ye la «coordenada angular» o «ángulu polar».

Nel casu del orixe, O, el valor de r ye cero, pero'l valor de θ ye indefiníu. N'ocasiones adopta la convención de representar l'orixe por (0,0º).

Historia

Magar esisten testimonios de que los conceutos d'ángulu y radiu conócense y remanen dende l'antigüedá, nun ye sinón hasta'l sieglu XVII, posterior a la invención de la xeometría analítica, cuando puede falase del conceutu formal de sistema coordenaes polares.

Los primeros usos empíricos de rellaciones ente ángulos y distancies rellacionar con aplicaciones al navegación y l'estudiu de la bóveda celeste. L'astrónomu Hiparco (190 e.C. -120 e.C. ) creó una tabla trigonométrica que daba'l llargor d'una cuerda en función del ángulu. Tamién esisten referencies del usu de coordenaes polares pa establecer la posición de les estrelles.^[1] Nel tratáu Sobre les espirales, Arquímedes describe la llamada espiral de Arquímedes, una función que'l so radiu depende del ángulu. Sicasí, estes aplicaciones nun faíen usu d'un sistema de coordenaes como mediu d'alcontrar puntos nel planu, situación análoga al estáu de la xeometría antes de la invención de la xeometría analítica.

En tiempos modernos, Grégoire de Saint-Vincent y Bonaventura Cavalieri introducieron de forma independiente'l conceutu de coordenada polar a mediaos del sieglu XVII na solución de problemes xeométricos. Saint-Vincent escribió sobre esta tema en 1625 y publicó los sos trabayos en 1647, ente que Cavalieri publicó los sos escritos en 1635 y una versión correxida en 1653. Cavalieri utilizó en primer llugar les coordenaes polares pa resolver un problema rellacionáu cola área dientro d'una espiral de Arquímedes. Blaise Pascal utilizó darréu les coordenaes polares pa calcular el llargor d'arcos parabólicos.

Sicasí, el conceutu astractu de sistema de coordenada polar deber a sir Isaac Newton, quien nel so Métodu de les flusiones escritu en 1671 y publicáu en 1736, introduz ocho nuevos sistemes de coordenaes (amás de les cartesianes) pa resolver problemes relativos a tanxentes y curves, unu de los cualos, el séptimu, ye'l de coordenaes polares.^[2] Nel periódicu Acta Eruditorum Jacob Bernoulli utilizó en 1691 un sistema con un puntu nuna llinia, llamándolos polu y exa polar respeutivamente. Les coordenaes determinar por aciu la distancia al polu y l'ángulu respeuto al exa polar. El trabayu de Bernoulli sirvió de base p'atopar el radiu de combadura de ciertes curves espresaes nesti sistema de coordenaes.

El términu actual de coordenaes polares atribuyir a Gregorio Fontana, y foi utilizáu polos escritores italianos del sieglu XVIII. El términu apaez per primer vegada n'inglés na traducción de 1816 efectuada por George Peacock del Tratáu del cálculu diferencial y del cálculu integral de Sylvestre François Lacroix,^[3] ente qu'Alexis Clairaut foi'l primeru que pensó n'ampliar les coordenaes polares a tres dimensiones.

Representación de puntos con coordenaes polares

Na figura representa un sistema de coordenaes polares nel planu, el centru de referencia (puntu O) y la llinia OL sobre la que se miden los ángulos. Pa referenciar un puntu indica la distancia al centru de coordenaes y l'ángulu sobre la exa OL.

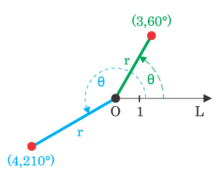
El puntu (3, 60º) indica que ta a una distancia de 3 unidaes dende O, midíes con un ángulu de 60º sobre OL.
El puntu (4, 210º) indica que ta a una distancia de 4 unidaes dende O y un ángulu de 210º sobre OL.

Un aspeutu a considerar nos sistemes de coordenaes polares ye qu'un únicu puntu del planu puede representase con un númberu infinitu de coordenaes distintes, lo cual nun asocede nel sistema de coordenaes cartesianes. Esto ye que nel sistema de coordenaes polares nun hai una correspondencia biunívoca ente los puntos del planu y el conxuntu de les coordenaes polares. Esto asocede por dos motivos:

Un puntu, definíu por un ángulu y una distancia, ye'l mesmu puntu que l'indicáu por esi mesmu ángulu más un númberu de revoluciones completes y la mesma distancia. Polo xeneral, el puntu ( $r$ , θ) puede representase como ( $r$ , θ ± $n$ ×360°) o (− $r$ , θ ± (2 $n$ + 1)180°), onde $n$ ye un númberu enteru cualesquier.^[4]
El centru de coordenaes ta definíu por una distancia nula, independientemente de los ángulos que s'especifiquen. De normal utilícense les coordenaes arbitraries (0, θ) pa representar el polu, yá que independientemente del valor que tome l'ángulu θ, un puntu con radiu 0 atópase siempres nel polu.^[5] Estes circunstancies tienen de tenese en cuenta pa evitar tracamundios nesti sistema de coordenaes. Pa llograr una única representación d'un puntu, suelse llindar $r$ a númberos non negativos $r$ ≥ 0 y θ al intervalu [0, 360°) o (−180°, 180°] (en radianes, [0, 2π) o (−π, π]).^[6]

Los ángulos en notación polar esprésense de normal en graos o en radianes, dependiendo del contestu. Por casu, les aplicaciones de navegación marítima utilicen les midíes en graos, ente que delles aplicaciones físiques (especialmente la mecánica rotacional) y la mayor parte del cálculu matemáticu espresen les midíes en radianes.^[7]

Conversión de coordenaes

Pasu de coordenaes polares a rectangulares y viceversa

Nel planu d'exes xy con centru de coordenaes nel puntu O puede definise un sistema de coordenaes polares d'un puntu M del planu, definíes pola distancia r al centru de coordenaes, y l'ángulu $\theta$ del vector de posición sobre la exa x.

Conversión de coordenaes polares a rectangulares

Definíu un puntu en coordenaes polares pol so ángulu $\theta$ sobre la exa x, y la so distancia r al centru de coordenaes, tiense:

x=r\cos \theta \,

y=r\operatorname {sen} \theta \,

Conversión de coordenaes rectangulares a polares

Definíu un puntu del planu poles sos coordenaes rectangulares (x,y), tiense que la coordenada polar r ye:

r={\sqrt {x^{2}+y^{2}}}

(aplicando'l Teorema de Pitágoras)

Pa determinar la coordenada angular θ, tienen d'estremase dos casos:

Pa $r$ = 0, l'ángulu θ puede tomar cualesquier valor real.
Pa $r$ ≠ 0, pa llograr un únicu valor de θ, tien de llindase a un intervalu de tamañu 2π. Por convención, los intervalos utilizaos son [0, 2π) y (−π, π].

Pa llograr θ nel intervalu [0, 2π), tienen d'usase les siguientes fórmules ( $\arctan$ denota la inversa de la función tanxente):

\theta ={\begin{cases}\arctan({\frac {y}{x}})&{\text{si }}x>0{\text{ y }}y\geq 0\\{\frac {\pi }{2}}&{\text{si }}x=0{\text{ y }}y>0\\\arctan({\frac {y}{x}})+\pi &{\text{si }}x<0\\{\frac {3\pi }{2}}&{\text{si }}x=0{\text{ y }}y<0\\\arctan({\frac {y}{x}})+2\pi &{\text{si }}x>0{\text{ y }}y<0\end{cases}}

Pa llograr $\theta$ nel intervalu $(-\pi ,\pi ]$ , considérase que $\arctan {\bigg (}{\frac {y}{x}}{\bigg )}\in {\bigg (}-{\frac {\pi }{2}},{\frac {\pi }{2}}{\bigg )}$ ye una función creciente nel so dominiu:

\theta ={\begin{cases}\arctan({\frac {y}{x}})-\pi &{\text{si }}x<0{\text{ y }}y<0\\-{\frac {\pi }{2}}&{\text{si }}x=0{\text{ y }}y<0\\\arctan({\frac {y}{x}})&{\text{si }}x>0\\{\frac {\pi }{2}}&{\text{si }}x=0{\text{ y }}y>0\\\arctan({\frac {y}{x}})+\pi &{\text{si }}x<0{\text{ y }}y\geq 0\end{cases}}

Munchos llinguaxes de programación modernos eviten tener qu'almacenar el signu del numberador y del denominador gracies a la implementación de la función arreyen2, que tien argumentos separaos pal numberador y el denominador. Nos llinguaxes que dexen argumentos opcionales, la función arreyen puede recibir como parámetru la coordenada x (como asocede en Lisp).

Ecuaciones polares

Llámase-y ecuación polar a la ecuación que define una curva espresada en coordenaes polares. En munchos casos puede especificase tal ecuación definiendo $r$ como una función de θ. La curva resultante consiste nuna serie de puntos na forma ( $r$ (θ), θ) y puede representase como la gráfica d'una función $r$ .

Pueden deducise distintes formes de simetría de la ecuación d'una función polar $r$ . Si $r$ (−θ) = $r$ (θ) la curva va ser simétrica respectu a la exa horizontal (0°/180°), si $r$ (180°−θ) = $r$ (θ) va ser simétrica respectu a la exa vertical (90°/ 270°), y si $r$ (θ−α°) = $r$ (θ) va ser simétricu rotacionalmente α° en sentíu horariu respectu al polu.

Por cuenta de la naturaleza circular del sistema de coordenaes polar, munches curves pueden describise con una simple ecuación polar, ente que na so forma cartesiana sería muncho más entrevesgáu. Dalgunes de les curves más conocíes son la rosa polar, la espiral de Arquímedes, la lemniscata, el cascoxu de Pascal y la cardioide.

Pa los apartaos siguientes entiéndese que'l círculu, la llinia y la rosa polar nun tienen restricciones nel dominiu y rangu de la curva.

Circunferencia

La ecuación xeneral pa una circunferencia con centru en ( $r$ ₀, φ) y radiu $a$ ye

r^{2}-2rr_{0}\cos(\theta -\varphi )+r_{0}^{2}=a^{2}.\,

En ciertos casos específicos, la ecuación anterior puede simplificase. Por casu, pa una circunferencia con centru nel polu y radiu a, llógrase:^[8]

r(\theta )=a\,

Llinia

Les llinies radiales (aquelles que traviesen el polu) representar por aciu la ecuación

\theta =\varphi \,

onde φ ye l'ángulu d'elevación de la llinia, esto ye, φ = arctan $m$ onde $m$ ye la pendiente de la llinia nel sistema de coordenaes cartesianes. La llinia non radial que crucia la llinia radial θ = φ perpendicularmente al puntu ( $r$ ₀, φ) tien la ecuación

r(\theta )={r_{0}}\sec(\theta -\varphi ).\,

Rosa polar

La rosa polar ye una famosa curva matemática que paez una flor con pétalos, y puede espresase como una ecuación polar simple,

r(\theta )=a\cos(k\theta +\phi _{0})\,

pa cualesquier constante $\phi _{0}$ (incluyendo al 0). Si k ye un númberu enteru, estes ecuaciones representen una rosa de k pétalos cuando k ye impar, o 2k pétalo si k ye par. Si k ye racional pero non enteru, la gráfica ye similar a una rosa pero colos pétalos asolapaos. Nótese qu'estes ecuaciones nunca definen una rosa con 2, 6, 10, 14, etc. pétalos. La variable a representa'l llargor de los pétalos de la rosa.

Si tomamos solu valores positivos pa r y valores nel intervalu $[0,2\pi )\,$ pa $\theta \,$ , la gráfica de la ecuación:

r(\theta )=\left|a\sin \left({\frac {k}{2}}\theta +\phi _{0}\right)\right|\,

ye una rosa de k pétalos, pa cualquier númberu natural $k\,$ . Y si $k=0\,$ , la gráfica ye una circunferencia de radiu $r=|a\sin(\phi _{0})|\,$

Espiral de Arquímedes

La espiral de Arquímedes ye una famosa espiral descubierta por Arquímedes, que puede espresase tamién como una ecuación polar simple. Representar cola ecuación

r(\theta )=a+b\theta .\,

Un cambéu nel parámetru a va producir un xiru na espiral, ente que b controla la distancia ente los brazos, que ye constante pa una espiral dada. La espiral de Arquímedes tien dos brazos, unu pa θ > 0 y otru pa θ < 0. Los dos brazos tán coneutaos nel polu. La imaxe especular d'un brazu sobre la exa vertical produz l'otru brazu. Esta curva foi una de les primeres curves, dempués de les seiciones cóniques, en ser descrites en trataos matemáticos. Amás ye'l principal exemplu de curva que puede representase de forma más fácil con una ecuación polar.

Otros exemplos d'espirales son la espiral logarítmica y la espiral de Fermat.

Seiciones cóniques

Elipse, indicándose la so semilado rectu.

Una seición cónica con un focu nel polu y l'otru en cualquier puntu de la exa horizontal (de cuenta que el semiexe mayor de la cónica fuelgue sobre la exa polar) ye dada por:

r={\ell  \over {1+y\cos \theta }}

onde y ye la escentricidá y $\ell$ ye'l semilado rectu (la distancia perpendicular a un focu dende la exa mayor a la curva). Si y > 1, esta ecuación define una hipérbola; si y = 1, define una parábola; y si y < 1, define una elipse. Pa la elipse, el casu especial y = 0 resulta nun círculu de radiu $\ell$ .

Númberos complexos

Ilustración d'un númberu complexu z nel planu complexu.

Cada númberu complexu puede representase como un puntu nel planu complexu, y puede espresase, por tanto, como un puntu en coordenaes cartesianes o en coordenaes polares. El númberu complexu z puede representase en forma rectangular como

z=x+iy\,

onde i ye la unidá imaxinaria. De forma alternativa, puede escribise en forma polar (por aciu les fórmules de conversión daes enriba) como

z=r\cdot (\cos \theta +i\operatorname {sen} \theta )

polo que se deduz que

z=re^{i\theta }\,

onde y ye la constante de Neper.^[9] Esta espresión ye equivalente a l'amosada na fórmula d'Euler. (Nótese que nesta fórmula, al igual qu'en toes aquelles nes qu'intervienen esponenciales d'ángulos, asumir que l'ángulu θ ta espresáu en radianes.) Pa pasar de la forma polar a la forma rectangular d'un númberu complexu dadu pueden usase les fórmules de conversión vistes enantes.

Pa les operaciones de multiplicación, división y exponenciación de númberos complexos, ye de normal muncho más simple trabayar con númberos complexos espresaos en forma polar que col so equivalente en forma rectangular:

Multiplicación:
$r_{0}y^{i\theta _{0}}\cdot r_{1}y^{i\theta _{1}}=r_{0}r_{1}y^{i(\theta _{0}+\theta _{1})}\,$
División:
${\frac {r_{0}y^{i\theta _{0}}}{r_{1}y^{i\theta _{1}}}}={\frac {r_{0}}{r_{1}}}y^{i(\theta _{0}-\theta _{1})}\,$
Exponenciación (Fórmula de De Moivre):
$(re^{i\theta })^{n}=r^{n}e^{in\theta }\,$

Cálculu infinitesimal

El cálculu infinitesimal pue ser aplicáu a les ecuaciones espresaes en coordenaes polares. A lo llargo d'esta seición espresa la coordenada angular θ en radianes, al ser la opción convencional nel analís matemáticu.^[10]^[11]

Cálculu diferencial

Partiendo de les ecuaciones de conversión ente coordenaes rectangulares y polares, y tomando derivaes parciales llógrase

r{\tfrac {\partial }{\partial r}}=x{\tfrac {\partial }{\partial x}}+y{\tfrac {\partial }{\partial y}}\,

{\tfrac {\partial }{\partial \theta }}=-y{\tfrac {\partial }{\partial x}}+x{\tfrac {\partial }{\partial y}}.

P'atopar la rimada en cartesianes de la recta tanxente a una curva polar r(θ) nun puntu dau, la curva tien d'espresase primero como un sistema d'ecuaciones paramétricas

x=r(\theta )\cos \theta \,

y=r(\theta )\operatorname {sen} \theta \,

Estremando dambes ecuaciones al respeutive de θ resulta

{\frac {dx}{d\theta }}=r'(\theta )\cos \theta -r(\theta )\operatorname {sen} \theta \,

{\frac {dy}{d\theta }}=r'(\theta )\operatorname {sen} \theta +r(\theta )\cos \theta .\,

Estremando la segunda ecuación pola primera llógrase la rimada cartesiana de la recta tanxente a la curva nel puntu (r, r(θ)):

{\frac {dy}{dx}}={\frac {r'(\theta )\operatorname {sen} \theta +r(\theta )\cos \theta }{r'(\theta )\cos \theta -r(\theta )\operatorname {sen} \theta }}.

Cálculu integral

Sía R una rexón del planu delimitada pola curva continua r(θ) y les semirrectas θ = a y θ = b, onde 0 < b − a < 2π. Entós, l'área de R vien dau por

S={\frac {1}{2}}\int _{a}^{b}r(\theta )^{2}\,d\theta .

Esta resultancia puede llograse de la siguiente manera. De primeres, l'intervalu [a, b] estremar en n subintervalos, onde n ye un enteru positivu cualesquier. Polo tanto Δθ, el llargor de cada subintervalo, ye igual a b − a (el llargor total del intervalu) estremáu por n (el númberu de subintervalos). Pa cada subintervalo i = 1, 2, …, n, seya θ_i el so puntu mediu. Puede construyise un sector circular con centru nel polu, radiu r(θ_i), ángulu central Δθ y llargor d'arcu $r(\theta _{i})\Delta \theta \,$ . L'área de cada sector ye entós igual a

S_{i}={\tfrac {1}{2}}r(\theta _{i})^{2}\Delta \theta

.

Poro, l'área total de tolos sectores ye

S_{n}=\sum _{i=1}^{n}S_{i}=\sum _{i=1}^{n}{\tfrac {1}{2}}r(\theta _{i})^{2}\,\Delta \theta .

Cuanto mayor seya n, meyor ye l'aproximamientu al área. Na llende, cuando n → ∞, la suma pasa a ser una suma de Riemann, y por tanto converxe na integral

\lim _{n\to +\infty }S_{n}={\frac {1}{2}}\int _{a}^{b}r(\theta )^{2}\mathrm {d} \theta =S

Xeneralización

Usando les coordenaes cartesianes, un elementu d'área infinitesimal pue ser calculáu como da = dx dy. El métodu d'integración per sustitución pa les integrales múltiples establez que, cuando s'utiliza otru sistema de coordenaes, tien de tenese en cuenta la matriz de conversión Jacobiana:

J=\det {\frac {\partial (x,y)}{\partial (r,\theta )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \theta }}\\{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \theta }}\end{vmatrix}}={\begin{vmatrix}\cos \theta &-r\operatorname {sen} \theta \\\operatorname {sen} \theta &r\cos \theta \end{vmatrix}}=r\cos ^{2}\theta +r\operatorname {sen} ^{2}\theta =r.

Poro, un elementu d'área en coordenaes polares puede escribise como:

da=J\,dr\,d\theta =r\,dr\,d\theta .

Una función en coordenaes polares pue ser integrada como sigue:

\iint _{R}f(r,\theta )\,da=\int _{a}^{b}\int _{0}^{r(\theta )}f(r,\theta )\,r\,dr\,d\theta .

onde R ye la rexón entendida por una curva r(θ) y les rectes θ = a y θ = b.

La fórmula pa l'área de R mentada enriba llógrase tomando f como una función constante igual a 1. Una de les aplicaciones d'estes fórmules ye'l cálculu de la Integral de Gauss : $\int _{-\infty }^{\infty }y^{-x^{2}}\,dx={\sqrt {\pi }}.$

Cálculu vectorial

El cálculu vectorial puede aplicase tamién a les coordenaes polares. Sía $\mathbf {r}$ el vector de posición $(r\cos \theta ,r\operatorname {sen} \theta )\,$ , con r y $\theta$ dependientes del tiempu t.

Sía : ${\hat {\mathbf {r} }}=(\cos \theta ,\operatorname {sen} \theta )$ .

un vector unitariu na direición de $\mathbf {r}$ y : ${\hat {\boldsymbol {\theta }}}=(-\operatorname {sen} \theta ,\cos \theta )$

un vector unitariu ortogonal a $\mathbf {r}$ . Les derivaes primer y segundo del vector de posición son:

{\frac {d\mathbf {r} }{dt}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}},

{\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+{\frac {1}{r}}\quad {\dot {\overbrace {r^{2}{\dot {\theta }}} }}\quad {\hat {\boldsymbol {\theta }}}

Estensión a más de dos dimensiones

Tres dimensiones

El sistema de coordenaes polares puede estendese a tres dimensiones con dos sistemes de coordenaes distintes: el sistema de coordenaes cilíndriques y el sistema de coordenaes esfériques. El sistema de coordenaes cilíndriques añade una coordenada de distancia, ente que'l sistema de coordenaes esfériques añade una coordenada angular.

Coordenaes cilíndriques

El sistema de coordenaes cilíndriques ye un sistema de coordenaes qu'estiende al sistema de coordenaes polares añadiendo una tercera coordenada que mide l'altor d'un puntu sobre'l planu, de la mesma forma que'l sistema de coordenaes cartesianes estender a tres dimensiones. La tercera coordenada suelse representar por h, faciendo que la notación de felicidaes coordenaes seya (r, θ, h).

Les coordenaes cilíndriques pueden convertise en coordenaes cartesianes de la siguiente manera:

{\begin{aligned}x&=r\,\cos \theta \\y&=r\,\operatorname {sen} \theta \\z&=h.\end{aligned}}

Coordenaes esfériques

Les coordenaes polares tamién pueden estendese a tres dimensiones usando les coordenaes (ρ, φ, θ), onde ρ ye la distancia al orixe, φ ye l'ángulu con respectu a la exa z (midíu de 0º a 180°), y θ ye l'ángulu con respectu a la exa x (igual que nes coordenaes polares, ente 0º y 360°) Esti sistema de coordenaes ye similar al sistema utilizáu pa denotar l'altitú y la llatitú d'un puntu na superficie de la Tierra, onde s'asitia l'orixe nel centru de la Tierra, la llatitú δ ye l'ángulu complementariu de φ (esto ye, δ = 90° − φ), y el llargor l vien dada por θ − 180°.^[12]

Les coordenaes esfériques pueden convertise en coordenaes cartesianes de la siguiente manera:

{\begin{aligned}x&=\rho \operatorname {sen} \phi \cos \theta \\y&=\rho \operatorname {sen} \phi \operatorname {sen} \theta \\z&=\rho \cos \phi \end{aligned}}

Les coordenaes polares nel espaciu tienen especial interés cuando los ángulos determinen la función, como nel casu de la héliz.

n dimensiones

Ye posible xeneralizar estes ampliaciones de forma que se llogre un sistema de representación pa 4 o más dimensiones. Por casu, pa 4 dimensiones llógrase : ${\begin{aligned}x&=\rho \operatorname {sen} \gamma \operatorname {sen} \phi \cos \theta \\y&=\rho \operatorname {sen} \gamma \operatorname {sen} \phi \operatorname {sen} \theta \\z&=\rho \operatorname {sen} \gamma \cos \phi \\t&=\rho \cos \gamma \end{aligned}}$

Aplicaciones

Les coordenaes polares son bidimensionales, polo que solamente se pueden usar onde les posiciones de los puntos asitiar nun planu bidimensional. Son les más fayadices en cualquier contestu onde'l fenómenu a considerar tea direutamente amestáu cola direición y llargor d'un puntu central, como nes figures de revolución, nos movimientos xiratorios, nes observaciones estelares, etc. Los exemplos vistos enantes amuesen la facilidá cola que les coordenaes polares definen curves como la espiral de Arquímedes, que la so ecuación en coordenaes cartesianes sería muncho más entrevesgada. Amás munchos sistemes físicos, tales como los rellacionaos con cuerpos que se mueven alredor d'un puntu central, o los fenómenos aniciaos dende un puntu central, son más simples y más intuitivos de modelar usando coordenaes polares. La motivación inicial de la introducción del sistema polar foi l'estudiu del movimientu circular y el movimiento orbital.

Posición y navegación

Les coordenaes polares úsense de cutiu en navegación, una y bones el destín o la direición del trayeutu pueden venir daos por un ángulu y una distancia al oxetu consideráu. Les aeronaves, por casu, utilicen un sistema de coordenaes polares llixeramente modificáu pa la navegación.

Modeláu

Los Sistemes son Busterniano simetría radial tienen unes carauterístiques fayadices pal sistema de coordenaes polares, col puntu central actuando como polu. Un primer exemplu d'esti usu ye la ecuación del fluxu de les agües soterrañes cuando s'aplica a pozos radialmente simétricos. De la mesma manera, los sistemes influyíos por una fuercia central son tamién bonos candidatos pal usu de les coordenaes polares. Dellos exemplos son les antenes radioeléctriques, o los campos gravitatorius, qu'obedecen a la llei de la inversa del cuadráu (vease'l problema de los dos cuerpos).

Los sistemes radialmente asimétricos tamién pueden modelase con coordenaes polares. Por casu la direutividad d'un micrófonu, que caracteriza la sensibilidá del micrófonu en función de la direición del soníu recibíu, puede representase por curves polares. La curva d'un micrófonu cardioide estándar, el más común de los micrófonos, tien por ecuación r = 0,5 + 0,5 sen θ.^[13]

Campos esguilares

Un problema nel analís matemáticu de funciones de delles variables ye la dificultá pa probar la esistencia d'una llende, yá que pueden llograse distintes resultaos según la trayeutoria d'aproximamientu al puntu. Nel orixe de coordenaes, unu de los puntos que tienen más interés pal analís (por anular davezu funciones racionales o logarítmiques), esti problema puede arreglase aplicando coordenaes polares. N'otros puntos ye posible realizar un cambéu de sistema de referencia y asina aplicar el trucu.

Al sustituyir les coordenaes cartesianes x, y, z... polos sos correspondientes equivalencies en coordenaes polares, la llende al averase al orixe amenorgar a una llende d'una única variable, lo que resulta bono de calcular por ser el senu y el cosenu funciones acutaes y r un infinitésimu. Si la resultancia nun amuesa dependencia angular, ye posible aseverar que la llende ye indistintu del puntu y trayeutoria dende'l que s'averó.

Ver tamién

Referencies

↑ Friendly, Michael. «Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization». Archiváu dende l'orixinal, el 24 d'avientu de 2008. Consultáu'l 10 de payares de 2008.
↑ Boyer, C. B. (1949). «Newton as an Originator of Polar Coordinates». American Mathematical Monthly 56. 10.2307/2306162, páxs. 73-78. http://www.jstor.org/pss/2306162.
↑ Smith, David Eugene (1925). History of Mathematics, Vol II. Boston: Ginn and Co., páx. 324.
↑ «Polar Coordinates and Graphing» (13 d'abril de 2006). Archiváu dende l'orixinal, el 2012-02-09. Consultáu'l 11 de xineru de 2009.
↑ David Cohen; David Sklar (2005) Thomson Brooks/Cole: Precalculus: With Unit-Circle Trigonometry, Cuarta Edición. ISBN 0534402305.
↑ Ian Stewart; David Tall (1983) Cambridge University Press: Complex Analysis (the Hitchhiker's Guide to the Plane). ISBN 0521287634.
↑ Raymond A. Serway; John W. Jewett, Jr. (2005) Brooks/Cole—Thomson Learning: Principles of Physics. ISBN 0-534-49143-X.
↑ Claeys, Johan. «Polar coordinates». Archiváu dende l'orixinal, el 27 d'abril de 2006. Consultáu'l 11 de xineru de 2009.
↑ Smith, Julius O.. «Euler's Identity», Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. ISBN 0-9745607-0-7.
↑ Husch, Lawrence S.. «Areas Bounded by Polar Curves». Archiváu dende l'orixinal, el 2000-03-01. Consultáu'l 11 de xineru de 2009.
↑ Lawrence S. Husch. «Tangent Lines to Polar Graphs». Archiváu dende l'orixinal, el 2019-11-21. Consultáu'l 11 de xineru de 2009.
↑ Wattenberg, Frank. «Coordenaes esfériques». Archiváu dende l'orixinal, el 22 d'avientu de 2008. Consultáu'l 26 de payares de 2008.
↑ Eargle, John (2005). Springer: Handbook of Recording Engineering, Fourth Edition. ISBN 0387284702.

Enllaces esternos

Wikimedia Commons tien conteníu multimedia tocante a Coordenaes polares.

[milestones-1] Friendly, Michael. «Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization». Archiváu dende l'orixinal, el 24 d'avientu de 2008. Consultáu'l 10 de payares de 2008.

[2] Boyer, C. B. (1949). «Newton as an Originator of Polar Coordinates». American Mathematical Monthly 56. 10.2307/2306162, páxs. 73-78. http://www.jstor.org/pss/2306162.

[3] Smith, David Eugene (1925). History of Mathematics, Vol II. Boston: Ginn and Co., páx. 324.

[4] «Polar Coordinates and Graphing» (13 d'abril de 2006). Archiváu dende l'orixinal, el 2012-02-09. Consultáu'l 11 de xineru de 2009.

[5] David Cohen; David Sklar (2005) Thomson Brooks/Cole: Precalculus: With Unit-Circle Trigonometry, Cuarta Edición. ISBN 0534402305.

[6] Ian Stewart; David Tall (1983) Cambridge University Press: Complex Analysis (the Hitchhiker's Guide to the Plane). ISBN 0521287634.

[7] Raymond A. Serway; John W. Jewett, Jr. (2005) Brooks/Cole—Thomson Learning: Principles of Physics. ISBN 0-534-49143-X.

[ping-8] Claeys, Johan. «Polar coordinates». Archiváu dende l'orixinal, el 27 d'abril de 2006. Consultáu'l 11 de xineru de 2009.

[9] Smith, Julius O.. «Euler's Identity», Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. ISBN 0-9745607-0-7.

[10] Husch, Lawrence S.. «Areas Bounded by Polar Curves». Archiváu dende l'orixinal, el 2000-03-01. Consultáu'l 11 de xineru de 2009.

[11] Lawrence S. Husch. «Tangent Lines to Polar Graphs». Archiváu dende l'orixinal, el 2019-11-21. Consultáu'l 11 de xineru de 2009.

[12] Wattenberg, Frank. «Coordenaes esfériques». Archiváu dende l'orixinal, el 22 d'avientu de 2008. Consultáu'l 26 de payares de 2008.

[13] Eargle, John (2005). Springer: Handbook of Recording Engineering, Fourth Edition. ISBN 0387284702.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]