Hipérbola

Hipérbola
	non-degenerate conic section (en) y espiral sinusoidal (es)

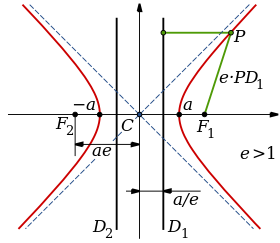
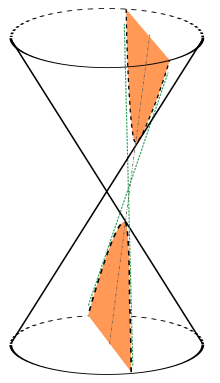
Una hipérbola (del griegu ὑπερβολή) ye una seición cónica, una curva abierta de dos rames llograda cortando un conu rectu por un planu oblicuu a la exa de simetría, y con ángulu menor que'l de la generatriz respectu de la exa de revolución.^[1]

Una hipérbola ye'l llugar xeométricu de los puntos d'un planu tales que'l valor absolutu de la diferencia de les sos distancies a dos puntos fixos, llamaos focos, ye igual a la distancia ente los vértices, que ye una constante positiva.

Etimoloxía. Hipérbole ya hipérbola

Hipérbola deriva de la pallabra griega ὑπερβολή (escesu), y ye cognáu de hipérbole (la figura lliteraria qu'equival a desaxeración).

Historia

Según la tradición, les seiciones cóniques fueron afayaes por Menecmo, nel so estudiu del problema de la duplicación del cubu,^[2] onde demuestra la esistencia d'una solución por aciu la corte d'una parábola con una hipérbola, lo cual ye confirmáu darréu por Proclo y Eratóstenes.^[3]

Sicasí, el primeru n'usar el términu hipérbola foi Apolonio de Perge nel so tratáu Cóniques,^[4] considerada obra cume sobre la tema de les matemátiques griegues, y onde se desenvuelve l'estudiu de les tanxentes a seiciones cóniques.

Ecuaciones de la hipérbola

Ecuaciones en coordenaes cartesianes: Ecuación d'una hipérbola con centru nel orixe de coordenaes $(0,0)\,$ y ecuación de la hipérbola na so forma canónica.

{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1

Ecuación d'una hipérbola con centru nel puntu $(h,k)\,$

{\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1

Exemplos:

a)

{\frac {(x)^{2}}{25}}-{\frac {(y)^{2}}{9}}=1

b)

{\frac {(y)^{2}}{9}}-{\frac {(x)^{2}}{25}}=1

Si la exa x ye positivu, entós la hipérbola ye horizontal; si ye al aviesu, ye vertical. La escentricidá d'una hipérbola siempres ye mayor qu'unu.

Ecuación de la hipérbola na so forma complexa

Una hipérbola nel planu complexu ye'l llugar xeométricu formáu por un conxuntu de puntos $z\,$ , nel planu $ReIm\,$ ; tales que, cualesquier d'ellos satisfai la condición xeométrica de que'l valor absolutu de la diferencia de les sos distancies $|z-w_{1}|-|z-w_{2}|\,$ , a dos puntos fixos llamaos focos $w_{1}\,$ y $w_{2}\,$ , ye una constante positiva igual al doble de la distancia (esto ye $2l\,$ ) qu'esiste ente'l so centru y cualesquier de los sos vértices de la exa focal.

La ecuación queda: $|z-w_{1}|-|z-w_{2}|=2l\,$

Evidentemente esta operación llevar a cabu nel conxuntu de los númberos complexos.

Ecuaciones en coordenaes polares

Dos hipérboles y los sos asíntotas en coordenaes cartesianes.

Hipérbola abierta de derecha a esquierda:

r^{2}=a\sec 2\theta \,

Hipérbola abierta de riba abaxo:

r^{2}=-a\sec 2\theta \,

Hipérbola abierta de nordés a suroeste:

r^{2}=a\csc 2\theta \,

Hipérbola abierta de noroeste a sureste:

r^{2}=-a\csc 2\theta \,

Hipérbola con orixe nel focu derechu:

$r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1-\varepsilon \cos \theta }}$

Hipérbola con orixe nel focu esquierdu:

$r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1+\varepsilon \cos \theta }}$

Ecuaciones paramétricas

Hipérbola abierta de derecha a esquierda:

{\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=\pm a\cosh t+h\\y=b\sinh t+k\\\end{matrix}}

Hipérbola abierta de riba abaxo:

{\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=a\sinh t+h\\y=\pm b\cosh t+k\\\end{matrix}}

En toles fórmules (h,k) son les coordenaes del centru de la hipérbola, a ye'l llargor del semiexe mayor, b ye'l llargor del semiexe menor.

Elementos de la hipérbola

Exa mayor o real

La exa mayor ye la recta de la hipérbola onde pertenecen los focos y los vértices de la mesma. El so valor ye 2a y ye perpendicular a la exa imaxinaria

Exa menor o imaxinariu

La exa menor o imaxinariu nun tien puntos de mancomún cola hipérbola. Sicasí, siempres se cumple que les perpendiculares llanzaes pelos sos estremos corten coles perpendiculares llanzaes pelos estremos de la exa mayor en 4 puntos que pueden sirvir pa trazar les asíntotas.

Asíntotas

Son les rectes r y r' que pasen pel centru de la hipérbola y verifiquen que s'averen a les cañes al alloñar del centru de la hipérbola.

Les ecuaciones de les asíntotas son: r: y= b/a x r': y = -b/a r

Vértices

Los vértices d'una hipérbola son los puntos onde esta curtia a les sos exes.

Focos

Son dos puntos, $F_{1}\,y\,F_{2}$ , respectu de los cualos permanez constante la diferencia de distancies (en valor absolutu) a cualquier puntu, $x$ , de dicha hipérbola.

\vert d(F_{1},x)-d(F_{2},x)\vert =cte

Centro

Puntu mediu de los vértices y de los focos de la hipérbola.

Tanxentes

La tanxente a una hipérbola en cualquier puntu de la curva ye bisectriz del ángulu formáu pelos radios vectores d'esi puntu.

Radiu de combadura

Sía'l puntu $M(x_{0},y_{0})$ de la hipérbola, entós el radiu de combadura ye

$R=a^{2}b^{2}({\frac {x_{0}^{2}}{a^{4}}}+{\frac {y_{0}^{2}}{b^{4}}})^{\frac {3}{2}}={\frac {(r_{1}\cdot r_{2})^{1.5}}{ab}}$

, la ecuación de la hipérbola ye

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

^[5]

Árees

01.Sía'l segmentu $AMN$ onde A, vértiz d'una caña; M y N estremos d'una cuerda perpendicular a la exa focal, entós l'área ye

$AMN=x\cdot y-a\cdot b\cdot \ln \left({\frac {x}{a}}+{\frac {y}{b}}\right)=a\cdot b\cdot \operatorname {Arch} {\frac {x}{a}}$

02. Sía'l cuadriláteru curvu $OAMG$ , onde O (orixe de coordenaes); segmentu OG sobre una asíntota; OA estremos centru y un vértiz; y $M(xy)$ un puntu de la hipérbola; MA un arcu d'hipérbola; L'área ye

$OAMG={\frac {a\cdot b}{4}}+{\frac {a\cdot b}{2}}\cdot \ln {\frac {2OG}{c}}$ ^[6]

Ver tamién

Referencies

↑ Si l'ángulu de planu interseición, respectu de la exa de revolución, ye mayor que l'entendíu ente la generatriz y la exa de revolución, la interseición va ser una elipse. Va Ser una parábola si ye paralelu a la citada exa, y una circunferencia si ye perpendicular a la exa.
↑ Heath, Sir Thomas (1921). A history of Greek Mathematics vol. 1 (n'inglés). Londres, Inglaterra: Oxford University Press. OCLC 2014918.
↑ Ken Schmarge. «Conic Sections in Ancient Greece» (inglés). Consultáu'l 2 de xunu de 2008.
↑ J. J. O'Connor y Y. F. Robertson. «Apollonius of Perga» (inglés). Consultáu'l 2 de xunu de 2008.
↑ Bronshtein et al Manual de matemátiques pa inxenieros y estudiantes Editorial Mir Moscú (1973)
↑ Bronshtein Op. cit.

Enllaces esternos

Exercicios resueltos y videu tutoriales sobre hipérbola
Animación d'un planu seicionando un conu y determinando la curva cónica hipérbola (enllaz rotu disponible n'Internet Archive; ver l'historial y la última versión).
Apollonius' Derivation of the Hyperbola at Convergence
Plantía:Planetmath reference
Plantía:Planetmath reference
Plantía:Planetmath reference
Weisstein, Eric W. «Hipérbola» (inglés). MathWorld. Wolfram Research.

[1] Si l'ángulu de planu interseición, respectu de la exa de revolución, ye mayor que l'entendíu ente la generatriz y la exa de revolución, la interseición va ser una elipse. Va Ser una parábola si ye paralelu a la citada exa, y una circunferencia si ye perpendicular a la exa.

[Heath-2] Heath, Sir Thomas (1921). A history of Greek Mathematics vol. 1 (n'inglés). Londres, Inglaterra: Oxford University Press. OCLC 2014918.

[3] Ken Schmarge. «Conic Sections in Ancient Greece» (inglés). Consultáu'l 2 de xunu de 2008.

[4] J. J. O'Connor y Y. F. Robertson. «Apollonius of Perga» (inglés). Consultáu'l 2 de xunu de 2008.

[5] Bronshtein et al Manual de matemátiques pa inxenieros y estudiantes Editorial Mir Moscú (1973)

[6] Bronshtein Op. cit.

[1]

[2]

[3]

[4]

[5]

[6]