Triángulu
| Triángulu | ||||
|---|---|---|---|---|
|
figura geométrica (es) | ||||
|
polígono bicéntrico (es) | ||||
 | ||||
| ||||
Un triángulu, en xeometría plana, ye un polígonu de tres llaos y tres ángulos. Los puntos comunes a cada par de llaos llámense vértices del triángulu.[1]
Un triángulu tien tres ángulos interiores, tres pares congruentes d'ángulos esteriores,[2] tres llaos y tres vértices, entre otros elementos.
Si ta conteníu nuna superficie plana se denomina triángulu, o trígonu (un nome menos común pa esta triba de polígonos). Si ta conteníu nuna superficie esférica se denomina triángulu esféricu. Representáu, en cartografía, sobre la superficie terrestre, llámase triángulu xeodésicu.
Tribes de triángulos[editar | editar la fonte]
Pola llonxitú de los llaos pueden clasificase en:
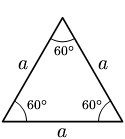
- Triángulu equilláteru: Los tres llaos tienen la mesma llonxitú y los ángulos de los vértices miden lo mesmo (60°)
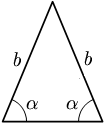
- Triángulu isósceles: Tien dos llaos y dos ángulos iguales
- Triángulu escalenu: Tolos llaos y tolos sos ángulos son desemeyaos.
|
|

|
|---|---|---|
| Equilláteru | Isósceles | Escalenu |
Pola midida de los sos ángulos:
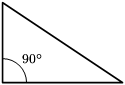
- Triángulu rectángulu: Tien un ángulu reutu (90º). A los dos llaos qu'ensamen un ángulu reutu nómase-yos catetos y al llau restante hipotenusa.
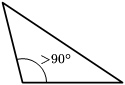
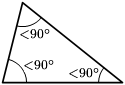
- Triángulu obtusángulu: ún de los sos ángulos ye obtusu (mayor de 90º) y los otros dos son agudos (menor de 90º)
- Triángulu acutángulu: Ye nel que los tres ángulos son menores a noventa. En particular, el triángulu equiláteru ye un exemplu de triángulu acutángulu.
- Triángulu oblicuángulu: Cuando nun tien un ángulu interior reutu (90º), ye dicir, que seya obtusángulu o acutángulu.
|
|
|
|---|---|---|
| Rectángulu | Obtusángulu | Acutángulu |
| Oblicuángulos | ||
Resume[editar | editar la fonte]
Según lo anterior los triángulos acutángulos son:
- Triángulu equilláteru, colos tres ángulos agudos ya iguales a 60º y los tres llaos iguales, esti triángulu ye simétricu respeutu a les sos tres altures.
- Triángulu acutángulu isósceles: con tolos ángulos agudos, siendo dos iguales, y el otru desemeyáu, esti triángulu ye simétricu respeutu de la so altura diferente.
- Triángulu acutángulu escalenu: con tolos sos ángulos agudos y toos diferentes, nun tien exes de simetría.
Los triángulos rectángulos pueden ser:
- Triángulu rectángulu isósceles: con un ángulu reutu y dos agudos iguales(de 45º cada ún), dos llaos son iguales y l'otru distintu, naturalmente los llaos iguales son los catetos , y el distintu ye la hipotenusa, ye simétricu respeutu a l'altura que pasa pol ángulu reutu hasta la hipotenusa.
- Triángulu rectángulu escalenu: tien un ángulu reutu y tolos sos llaos y ángulos son diferentes.
Los triángulos obtusángulos son:
- Triángulu obtusángulu isósceles: tien un ángulu obtusu, y dos llaos iguales que son los que parten del ángulu obtusu, l'otru llau ye mayor qu'estos dos.
- Triángulu obtusángulu escalenu: tien un ángulu obtusu y tolos sos llaos son distintos.
| Triángulu | |||
|---|---|---|---|
| acutángulu | 
|

|

|
| rectángulu | 
|

| |
| obtusángulu | 
|

|
Cálculu de la superficie d'un triángulu[editar | editar la fonte]
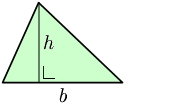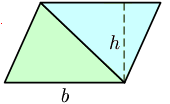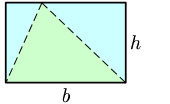
- La superficie o l'área (xeometría) d'un triángulu obtiénse multiplicando la base pola altura (au l'altor ye un segmentu perpendicular que va dende la base hasta'l vértiz opuestu) y dixebrando por dos. Siendo b la llonxitú de cualquiera de los llaos del triángulu y h la distancia perpendicular ente la base y el vértiz opuestu a esa base, la superficie S queda del siguiente mou:
- Si conocemos les llonxitúes de los llaos del triángulu (a, b, c) ye dable calcular la superficie emplegando la fórmula d'Herón.
onde p = ½ (a + b + c) ye'l semiperimetru del triángulu.
Cuando el triángulu ye enforma "afiláu" (la suma de los dos llaos menores ye abondo asemeyada al valor del llau mayor) la fórmula anterior ye inestable numbéricamente.
Reescribiendo la fórmula anterior tenemos: (suponiendo a ≥ b ≥ c )
Los paréntesis eviten la inestabilidá na fórmula.
Propiedaes de los triángulos.[editar | editar la fonte]
- Una propiedá obvia de tolos triángulos ye que la suma de les llonxitúes de dos de los sos llaos, ye siempre mayor que la llonxitú del tercer llau.
- La suma de tolos ángulos de los sos vértices, nún planu, ye igual a 180°.

- Pa cualquier triángulu rectángulu cuyos catetos midan a y b, y cuya hipotenusa mida c, verifícase que:(Teorema de Pitágores)
- a² + b² = c²
- Pa cualquier triángulu verifícase'l Teorema del senu que demuestra que: «Los llaos d'un triángulu son proporcionales a los senos de los ángulos opuestos»:
- Pa cualquier triángulu verifícase'l Teorema del cosenu que demuestra que: «El cuadráu d'un llau ye igual a la suma de los cuadraos de los otros llaos menos el duble del productu d'estos llaos pol cosenu del ángulu comprendíu»:
Centros del triángulu[editar | editar la fonte]
Xeométricamente puen definise dellos centros nún triángulu:
- Baricentru: ye'l puntu que s'alcuentra na interseición de les medianes, y equival al centru de gravedá
- Circuncentru: ye'l centro de la circunferencia circunscrita, aquella que pasa polos tres vértices del triángulu. Allúgase na interseición de les mediatrices de los llaos.
- Incentru: ye'l centru de la circunferencia inscrita, aquella que ye tanxente a los llaos del triángulu. Allúgase na interseición de les bisectrices de los ángulos.
- Ortocentru: ye'l puntu que s'afaya na interseición de les altures.
L'únicu casu nel que los tolos centros coinciden nún únicu puntu, ye nún triángulu equilláteru.
Triángulos Oblicuángulos[editar | editar la fonte]
Pa resolver triángulos oblicuángulos utilízase'l Teorema del Senu y el Teorema del cosenu.
Ver tamién[editar | editar la fonte]
 Wikimedia Commons tien conteníu multimedia tocante a triángulos.
Wikimedia Commons tien conteníu multimedia tocante a triángulos.- Puntos d'Euler
- Teorema de Pitágores
- Teorema del senu
- Teorema del cosenu
- Vértiz
Referencies[editar | editar la fonte]
| Polígonos |
|---|
| Triángulu • Cuadriláteru • Pentágonu • Hexágonu • Heptágonu • Octógonu • Eneágonu • Decágonu • Endecágonu • Dodecágonu • Tridecágonu • Tetradecágonu • Pentadecágonu • Hexadecágonu • Heptadecágonu • Octodecágonu • Eneadecágonu • Isodecágonu • Triacontágonu • Tetracontágonu • Pentacontágonu • Hexacontágonu • Heptacontágonu • Octocontágonu • Eneacontágonu • Hectágonu • Chiliágonu • Miriágonu • Megágonu • Googólgonu |








