Xiroscopiu
| Xiroscopiu | |
|---|---|
 | |

El xiroscopiu (del griegu skopeein, 'ver' y gyros, 'xiru') ye un dispositivu mecánicu que sirve pa midir, caltener o camudar la orientación nel espaciu de dalgún aparatu o vehículu.
Ta formáu esencialmente por un cuerpu con simetría de rotación que xira alredor de la exa de dicha simetría. Cuando'l xiroscopiu sométese a un momentu de fuercia que tiende a camudar la orientación de la so exa de rotación, tien un comportamientu aparentemente paradóxicu, yá que camuda d'orientación (o esperimenta un momentu angular sía que non, si ta acutáu) xirando respectu d'una tercer exa, perpendicular tantu a aquel respectu del cual emburriar a xirar, como a la so exa de rotación inicial. Si ta montáu sobre un soporte de Cardano qu'embrive cualesquier momentu angular esternu, o si a cencielles xira llibre nel espaciu, el xiroscopiu caltién la orientación de la so exa de rotación ante fuercies esternes que tiendan a esvialo meyor qu'un oxetu non xiratoriu; esviar muncho menos, y nuna direición distinta.
Presenta, por tanto, dos propiedaes fundamentales: la inercia xiroscópica o «rixidez nel espaciu» y la precesión, que ye l'enclín de la exa n'ángulu rectu ante cualquier fuercia que tienda a camudar el planu de rotación. Estes propiedaes manifestar a tolos cuerpos en rotación, incluyida la Tierra. El términu xiroscopiu aplícase xeneralmente a oxetos esféricos o en forma de discu montaos sobre una exa, de forma que puedan xirar llibremente en cualquier direición; estos preseos emplegar pa demostrar les propiedaes anteriores, pa indicar movimientos nel espaciu, o pa producilos.
Esti fenómenu físicu, el efeutu xiroscópicu, puede reparase fácil y cotidianamente en peonces, o monedes llanzaes a rodar, por casu, anque de xacíu, cualquier oxetu xiratoriu funciona en ciertu mou, como xiroscopiu. El xiru en vuelu impartíu pol xugador a un balón de rugbi, o'l d'una bala disparada dende una arma d'ánima rayada pa estabilizar la so trayeutoria son exemplos d'aplicación del efeutu.
Historia y aplicaciones[editar | editar la fonte]

La peonza o trompu ye de xuru l'elementu cultural más vieyu y senciellu qu'ilustra de forma clara l'efeutu xiroscópicu en funcionamientu. Nes sos diverses formes conocer dende bien antiguu, con restos y referencies pictóriques o epigráficas que daten siquier dende'l primer mileniu e.C., en Mesopotamia, anque de xuru sía bien anterior. Hai evidencies del so usu tempranu na Antigua Roma, en Grecia, China, India y munchos otros llugares. Permanez n'esencia un xuguete inalteráu, variando llixeramente la forma y los materiales (magre, madera, plásticu, metal, etc.) y la decoración. De xacíu, conocer empíricamente el so funcionamientu, el fechu de que al xirar caltiénse de pies, nun implica que se conocieren les causes del fenómenu, nin poder calcular la magnitú y los factores qu'inflúin nel efeutu, colo que les aplicaciones más potentes nun fueron evidentes hasta muncho más tarde, concluyida la revolución científica y escontra el final de la Revolución Industrial.

Al paecer, unu de los primeros intentos conocíos d'aplicación de les propiedaes de la peonza foi'l «espejillo xiratoriu» de John Serson, un capitán inglés. En 1743, inventó una especie de peonza que sirviría p'alcontrar l'horizonte n'alta mar, en condiciones de visibilidá amenorgada, gracies a la so estabilidá dinámica. Sería un precursor bien rudimentariu del horizonte artificial modernu, anque nun paez tener gran impautu.
A quien s'atribúi'l descubrimientu del efeutu xiroscópicu y la construcción del primer preséu paecíu al xiroscopiu modernu ye al astrónomu alemán Johann Bohnenberger, quien en 1817 escribió avera de la tema nun escritu tituláu Descripción d'una máquina pa la esplicación de les lleis de rotación de la Tierra en redol a la so exa, y del cambéu d'orientación del mesmu. Llamó al so aparatu, una esfera rotatoria pesada, "la máquina".[1] El matemáticu francés Siméon Denis Poisson yá menta[2] dicha máquina en 1813, nuna memoria so, y el so compatriota y colega Pierre-Simon Laplace, trabayando entós daquella na escuela politéunica de París, encamentó'l so usu na enseñanza, como ayuda didáctica. Asina foi como llegó a saber d'ella Léon Foucault.[3]
El xiroscopiu como tal foi inventáu, con esi mesmu nome, en 1852 por Foucault, montando una masa rotatorio nun soporte de Cardano pa un esperimentu de demostración de la rotación de la Tierra. La rotación yá fuera demostrada col pendilexu de Foucault. Sicasí nun entendía por qué la velocidá de rotación del pendilexu yera más lenta que la velocidá de rotación de la Tierra por un factor , onde representa la llatitú en que s'alcuentra'l pendilexu. Precisábase otru aparatu pa demostrar la rotación de la Tierra de forma más simple.

Foucault presentó asina un aparatu capaz de caltener una rotación abondo rápida (150 a 200 vueltes per minutu) mientres un tiempu abondu (una decena de minutos) por que pudieren faese midíes. Esta proeza mecánica (pa la dómina) ilustra'l talentu de Foucault y el so collaborador Froment en mecánica.

Foucault tamién se dio cuenta de que'l so aparatu podía sirvir pa indicar el Norte. N'efeutu, si torguen ciertos movimientos del soporte del xiroscopiu, ésti allíniase col meridianu. Esto dexó la invención del girocompás, una brúxula xiroscópica.
Otra de les sos aplicaciones industriales iniciales foi sirvir como sistema de guía a los primeres torpedos, dexando programar una rudimentaria ruta a siguir antes del llanzamientu y correxir les esviaciones sobre la marcha, hasta ciertu puntu. Polo xeneral emplegar enforma pa la navegación inercial n'aviones, misiles y similares construyíos antes de l'apaición del GPS (entá son imprescindibles, pero yá non como únicu o principal sistema d'empuestu, sinón pa controlar con precisión la orientación). Nesti campu últimamente empiecen a sustituyise por xiroscopios de fibra óptica, y en munches aplicaciones industrial y cotidianu, como la tableta o'l teléfonu intelixente, utilícense xiroscopios del tipu "MEMS" (Micro Electro Mechanical System), "SMLM" n'asturianu, con menor tamañu y pesu, y mayor precisión y cencellez, que namái comparten la función col xiroscopiu mecánicu, non l'efeutu xiroscópicu como principiu operativu.
Tamién s'utilicen xiroscopios mecánicos pa menguar el valumbu de navíos y p'estabilizar plataformes de tiru.
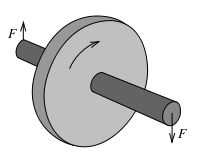
| Cuando se da un golpecito na estremidá de la barra horizontal comunicar a les mases una velocidá horizontal perpendicular a les sos velocidaes tanxenciales. | Vista dende enriba del dibuxu d'esquierda. Les velocidaes de la masa de riba tán dibuxaes en trazos continuos y les de la masa de baxo en puntiáu. |
Descripción del efeutu xiroscópicu[editar | editar la fonte]
Supongamos un xiroscopiu formáu por un discu montáu sobre una exa horizontal, alredor del cual el discu xira llibremente a gran velocidá, como se repara na figura de la derecha. Un observador caltién la exa del fondu cola manzorga y l'exa de lantre cola mano derecha. Si l'observador trata de faer xirar la exa escontra la derecha (baxando la mano derecha y xubiendo la manzorga) va sentir un comportamientu bien interesáu, una y bones el xiroscopiu emburria la so mano derecha y tira de la so manzorga. L'observador acaba de sentir l'efeutu xiroscópicu. Ye una sensación bien sorprendente porque da la impresión de que'l xiroscopiu nun se porta como un oxetu normal».
Descripción detallada del efeutu[editar | editar la fonte]
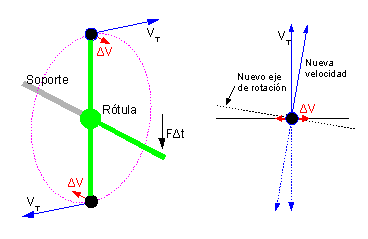
Sía l'oxetu dibuxáu na imaxe de la derecha, formáu por dos mases (en negru) de pequeñes dimensiones suxetes por una barra (en verde) en forma de T de masa despreciable y total rixidez. El centru de la T ta afitáu a un soporte per mediu d'una rótula que dexa que la barra en T xire llibremente alredor de cualquier exa.
Les mases xiren rápido alredor del puntu fixu con una velocidá tanxencial . Nel momentu que les mases pasen pola posición del dibuxu da un impulsu escontra baxo na estremidá llibre de la T. La barra verde tresmite esi impulsu a los dos mases y da-y a caúna, una pequeña velocidá horizontal perpendicular a la so velocidá actual. Escontra la derecha na masa de riba y escontra la esquierda na masa de baxo; esto ye, la barra xira un pocu respectu de la exa llonxitudinal.
Nel dibuxu de la derecha apaecen los dos mases vistes dende enriba. Les velocidaes comunicaes pol impulsu sumir a les velocidaes corrientes. La consecuencia inmediata ye que la velocidá de la masa de riba esviar llixeramente escontra la derecha y la velocidá de la masa de baxo esviar escontra la esquierda. Sorprendentemente, la resultancia final ye que'l planu de rotación de los dos mases xiró (amás de respectu de la exa llonxitudinal, tamién respectu de la exa vertical) O, dicho otra manera, la exa de rotación de los dos mases xiró respectu de dos exes, y non yá respectu del qu'intentábamos faelo xirar.
Nun xiroscopiu nun se trata de dos mases puntuales sinón de mases distribuyíes sobremanera'l discu o'l cilindru, pero eso nun camuda'l fondu de la esplicación. Y cuando, en llugar de da-y un impulsu a un xiroscopiu, aplícase-y un momentu, puede considerase esti momentu como una socesión de curtios impulsos. Cada unu d'ellos añade a les mases una ínfima velocidá perpendicular a les sos velocidaes. Eso fai que la velocidá camude de direición ensin camudar de módulu.

Esplicación intuitiva de la causa del efeutu xiroscópicu[editar | editar la fonte]
Supongamos frente a nós un xiroscopiu, un discu trevesáu per una exa. Imaginémoslo de forma tal que la exa atopar n'horizontal, frente a los nuesos güeyos, y nueses dos manes garren los estremos; por tanto, vamos ver el "cantar" del discu en vertical. Imaxinemos agora que'l discu empieza a xirar nel sentíu nel que la so parte cimera se "alloña" de nós y l'inferior se "avera" a nós. Imaxinemos por casu un puntu coloráu pintáu sobre'l cantar, de cuenta que lo vemos xirar col discu, va siempres de baxo a enriba al pasar frente a nós. Agora xubimos un pocu nuesa manzorga y baxamos un pocu la derecha, inclinando la exa de xiru del discu. Si agora miramos el nuesu puntu coloráu, vamos ver que yá nun viaxa de baxo a enriba, sinón en diagonal, esto ye, de baxo a enriba y d'esquierda a derecha. Agora estremamos mentalmente'l discu, ensin detenelo, en dos metaes: la más alloñada de nós (la metá del discu que nun vemos, dende la nuesa perspeutiva) y la más cercana (la que vemos), y damos cuenta de que, na parte más alloñada del discu, el puntu coloráu viaxa siempres escontra baxo y a la izquierda. Na más cercana, viaxa escontra riba y a la derecha. De xacíu, non yá el puntu coloráu, tola masa del discu sigue estes direiciones en cada metá. La componente vertical del movimientu (enriba o embaxo) podemos inorala, porque yá esistía antes d'inclinar la exa, anque yera mayor. Lo realmente nuevo son les componentes horizontales del movimientu. La masa ta moviéndose de derecha a esquierda na parte más alloñada del discu, y d'esquierda a derecha na más cercana, na que vemos. Estos movimientos de masa con una componente horizontal, qu'apaecen al inclinar la exa, anicien reacciones (3ª Llei de Newton) opuestes a ellos, y por tanto'l discu va esperimentar una fuercia escontra la derecha na so parte alloñada, y escontra la esquierda na so parte cercana. Ye dicir que les nueses manes, que sostienen la exa, al inclinalo, xubiendo la manzorga y baxando la derecha (amás de notar la resistencia habitual de sentíu opuestu al nuesu esfuerciu y que notaríamos anque'l discu nun xirara, 3ª Llei de N), van notar una fuercia "estraña" qu'emburria escontra tras la nuesa mano derecha, y palantre la esquierda. Esta fuercia, sorprendente y esconcertante pa quien nun conoz el fenómenu, ye l'efeutu xiroscópicu. Ye por esi nuevu momentu angular perpendicular al planu de rotación inicial pol que, si'l xiroscopiu nun ta acutáu nes sos exes de movimientu, al pretender xirar dichu planu esperimenta otra rotación (como reacción newtoniana a dichu momentu) tamién nuna tercer exa perpendicular al xiru y a la so exa de rotación inicial.
En resume, la causa del efeutu xiroscópicu ye'l cambéu na direición de desplazamientu de la masa del discu, con una componente paralela a la exa de rotación inicial, de sentíu contrariu en cada estremu del discu. Esta nueva componente del movimientu implica una reacción de sentíu contrariu (3ª Llei de Newton), que se manifiesta nel momentu angular qu'esperimenta'l xiroscopiu.

Esto vese entá más claru si sustituímos el discu del xiroscopiu, una vegada inclináu, por otros dos que los sos exes de xiru son ortogonales, como nes viñetes de la imaxe de baxo. El discu vertical representa'l momentu angular que se caltién nel planu de xiru inicial, y l'horizontal el que pasó a esti planu. Si'l xiroscopiu permanez vertical, nun hai rueda horizontal, namái equival a un discu vertical del so mesmu tamañu. Cuando empieza a inclinase, apaez el discu horizontal, de primeres bien pequeñu, en comparanza col vertical. A midida que el xiroscopiu va inclinándose, y escai l'ángulu, el tamañu de la rueda vertical menguaría, y aumentaría el de la horizontal. Rescampla que si los dos ruedes tán acoplaes nun únicu mecanismu, ésti va esperimentar un momentu angular nel planu horizontal, contrariu al sentíu de xiru del discu horizontal a midida que ésti creza en tamañu (y por tanto en momentu angular) pa caltener el caltenimientu del momentu angular del mecanismu total.
Movimientos del xiroscopiu y planteamientu matemáticu[editar | editar la fonte]
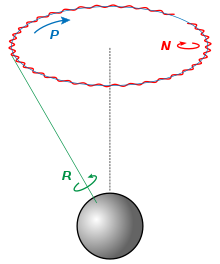
Acordies cola mecánica del sólidu ríxidu, amás de la rotación alredor de la so exa de simetría, un xiroscopiu presenta polo xeneral dos movimientos principales: la precesión y la nutación. Esti fechu deduzse direutamente de les ecuaciones de Euler.
Pa entender cuantitativamente el movimientu d'un xiroscopiu, podemos utilizar la segunda llei de Newton pa la rotación.
Xunto coles rellaciones
y
Onde Ι ye'l momentu d'inercia y ω ye la velocidá angular de la rueda al respeutive de la so exa de spin.
Nun xiroscopiu tenemos de tener en cuenta que'l cambéu nel momentu angular de la rueda tien de dase na direición del momentu de la fuercia qu'actúa sobre la rueda.
La velocidá angular de precesión puede calculase de la siguiente manera:
Nun pequeñu intervalu de tiempu dt, el cambéu esperimentáu enagora angular tien módulu dL:
Onde MgD ye'l módulu del momentu respeuto al puntu onde pivota. L'ángulu θ barríu pela exa nel so movimientu ye
Y por lo tanto la velocidá angular de precesión ye
Precesión[editar | editar la fonte]

Cuando s'aplica un momentu a un cuerpu en rotación que'l so momentu angular ye , y siempres que nun sía colineal col momentu angular orixinal , la direición de la exa de rotación del cuerpu animar d'un movimientu de rotación de velocidá angular . Esta velocidá angular, llamada velocidá de precesión, ta rellacionada col momentu y el momentu angular pola fórmula:
La velocidá de precesión, como toles velocidaes angulares, midir en radianes/segundu. En módulu, la velocidá de precesión ye igual a . Esto ye, para una mesma cantidá pel momento, la magnitú de la velocidá de precesión ye tantu más pequeña cuanto más grande sía'l momentu angular. Y como'l momentu angular ye'l productu de la velocidá de rotación del xiroscopiu multiplicada pol so momentu d'inercia, puede amenorgase la velocidá de precesión aumentando'l momentu d'inercia, la velocidá de rotación o dambes.
Equí atopamos l'interés d'utilizar un xiroscopiu pa caltener una referencia de direición. Partiendo del reposu, tolos cuerpos caltienen la orientación que tienen salvu cuando se-yos apliquen momentos esternos. Nesi casu, cuando un cuerpu non xira, l'efeutu del momentu ye'l de crear una aceleración angular, que crea una velocidá angular creciente. Cuando'l momentu atáyase, l'oxetu sigue xirando cola velocidá angular qu'adquirió. Sicasí, cuando'l mesmu momentu aplicar a un oxetu en rotación, este empieza a xirar cola velocidá de precesión calculada antes. Y cuando'l momentu atáyase, la precesión del oxetu tamién s'ataya. La resultancia ye que, nun xiroscopiu, los momentos parásitos tienen muncho menos efeutu al llargu plazu que nun oxetu ensin rotación. Amás, puede menguase l'efeutu d'esos momentos, aumentando'l momentu d'inercia y la velocidá de rotación del xiroscopiu.
Nutación[editar | editar la fonte]
Cuando'l momentu que causa la precesión camuda de valor, la velocidá de precesión tamién camuda de valor. Pero esi cambéu nun asocede instantáneamente. Hai un periodu de transición mientres el cual el xiroscopiu «dexa un mizcu al momentu na mesma direición qu'un oxetu que nun xira. Dempués el xiroscopiu repon lo que venciera, bazcuyando na direición del momentu alredor de la trayeutoria de precesión final. Esti movimientu d'oscilación transitoriu llámase nutación.
Si'l cambéu de valor de los momentos enllargar, la nutación puede durar enforma. Ye'l casu de la Tierra. L'atraición de la Lluna y del Sol sobre l'abombadura de la Tierra nel ecuador ye distintu ente'l llau próximu y el llau alloñáu respectu al astru. Esa diferencia d'atraición crea un momentu, que causa la precesión de los equinoccios. Pero, como nin el Sol nin la Lluna tán nel planu del ecuador terrestre, el momentu producíu por estos astros camuda dacuando y el movimientu de nutación de la Tierra non se amortigua.
Bicicleta[editar | editar la fonte]
Supúnxose mientres enforma tiempu que l'efeutu xiroscópicu yera l'únicu o'l principal fenómenu físicu rellacionáu col equilibriu de les bicicletes y motocicletes, anque foi delles vegaes refutado.[4] La forma más senciella de comprobar que l'efeutu xiroscópicu nun apurre la mayor parte de la so estabilidá a una bicicleta ye compensalo con xiroscopios nes ruedes. L'esperimentu foi realizáu[5] y comprobóse que la bicicleta ye perfectamente estable ensin efeutu xiroscópicu netu. Sicasí, ye imposible conducir una bicicleta col manillar bloquiáu, lo que demuestra que son les fuercies centrífugues (nel sistema de referencia de la bicicleta) qu'apaecen al mover el manillar les que-y confieren estabilidá. Una bicicleta o una motocicleta llanzaes en movimientu ensin conductor, siguen avanzando ensin cayese hasta qu'atopen una torga o que pierdan el so impulsu. La trayeutoria va ser una espiral, un círculu o, raramente, una recta.

Nel dibuxu ta representada una bicicleta en movimientu col manillar derechu ya inclinada un pocu escontra la esquierda. El pesu de la bicicleta crea un momentu que tiende a inclinar entá más la bicicleta y a faela cayer. Pero como la bicicleta avanza, la rueda de lantre tien un momentu angular empobináu escontra la esquierda. La rueda de tras tamién tien un momentu angular, pero la manera na cual ta suxeta nun-y dexa tener efeutu nel equilibriu de la bicicleta. Esti momentu crea una variación , dirixida escontra tras, del momentu angular de la rueda de lantre. Esto quier dicir que la rueda de lantre xira escontra la esquierda, como si xirárase'l manillar escontra la esquierda. La bicicleta empieza a voltiar escontra la esquierda. Mientres el momentu faiga inclinase más la bicicleta, el momentu angular de la rueda de lantre va inclinase escontra tras, el manillar escontra la esquierda y el radiu de la trayeutoria de la bicicleta va menguar.
Vistu dende'l sistema aceleráu y non inercial de la bicicleta, el radiu de rotación mengua, lo cual aumenta la fuercia centrífuga. Esta fuercia centrífuga crea un momentu que tiende a endrechar la bicicleta y a compensar el momentu del pesu que tiende a faela cayer. Cuando los dos momentos terminen per compensar se, la bicicleta dexa d'inclinase y el manillar de xirar escontra la esquierda. La bicicleta sigue na so trayeutoria circular con radio constante. Si'l frotamiento col aire o otres coses mengüen la velocidá de la bicicleta, la fuercia centrífuga va menguar, la bicicleta recomenzará a cayese, lo cual va faer xirar el manillar escontra la esquierda. El radiu de xiru va menguar, lo cual va aumentar la fuercia centrífuga hasta qu'ésta compense de nuevu'l momentu del pesu. Cuando'l manillar llega a 90° o se bloquia, la bicicleta caise.
Si llánzase una bicicleta col manillar inmovilizáu (amarráu), la bicicleta va cayese como si tuviera parada.
Ver tamién[editar | editar la fonte]
Referencies[editar | editar la fonte]
- ↑ Johann G. F. Bohnenberger (1817) "Beschreibung einer Maschine zur Erläuterung der Gesetze der Umdrehung der Erde um ihre Axe, und der Veränderung der Lage der letzteren" (Descripción d'una máquina pa la esplicación de les lleis de rotación de la Tierra en redol a la so exa, y del cambéu d'orientación del mesmu), Tübinger Blätter für Naturwissenschaften und Arzneikunde, vol. 3, páxines 72–83.
- ↑ El matemáticu francés Poisson menta la máquina de Bohnenberger yá en 1813: Simeon-Denis Poisson (1813) "Mémoire sur un cas particulier du mouvement de rotation des corps pesans" [Memoria sobre un casu particular del movimientu de rotación de los cuerpos pesaos.], Journal de l'École Polytechnique, vol. 9, páxines 247–262. Disponible n'Internet en: http://www.ion.org/museum/files/File_2.pdf .
- ↑ (N'inglés) Wagner JF, "La Máquina de Bohnenberger", Institutu de la Navegación. (Wagner JF, "The Machine of Bohnenberger", The Institute of Navigation)
- ↑ Klein, Richard E.. «Bicycle Science». Archiváu dende l'orixinal, el 10 de setiembre de 2007. Consultáu'l 4 d'agostu de 2006.
- ↑ Jones, David Y. H. (1970). «The stability of the bicycle». Physics Today 23 (4): páxs. 34–40. http://socrates.berkeley.edu/%7Efajans/Teaching/MoreBikeFiles/JonesBikeBW.pdf. Consultáu'l 4 d'agostu de 2006.
Bibliografía[editar | editar la fonte]
- Feynman, Leighton and Sands. Lectures on physics. Addison-Wesley. (n'inglés)
Enllaces esternos[editar | editar la fonte]
 Wikimedia Commons tien conteníu multimedia tocante a Xiroscopiu.
Wikimedia Commons tien conteníu multimedia tocante a Xiroscopiu.
- The Precession and Nutation of a Gyroscope (n'inglés) (Bien incompleta en 2006.)
- Everything you needed to know about gyroscopes (n'inglés)
- Cómo construyir Xiroscopios (n'español)
- Magnetal AB - Xiroscópico efeutu y el volante - un estudiu (n'inglés)

















