Sistema binariu
Esti artículu o seición necesita referencies qu'apaezan nuna publicación acreitada, como revistes especializaes, monografíes, prensa diaria o páxines d'Internet fiables. |
| Sistema binariu | ||||
|---|---|---|---|---|
|
sistema de numeración posicional (es) | ||||
| Códigu binariu | ||||
 | ||||
| ||||
El sistema binariu, llamáu tamién sistema diádicu[1] en ciencies de la computación, ye un sistema de numberación nel que los númberos represéntense utilizando solamente dos cifres: cero y unu (0 y 1). Ye unu de los sistemes que s'utilicen nos ordenadores, por cuenta de que estes trabayen internamente con dos niveles de voltaxe, polo cual el so sistema de numberación natural ye'l sistema binariu.[2]
Historia del sistema binariu[editar | editar la fonte]

L'antiguu matemáticu indiu Pingala presentó la primer descripción que se conoz d'un sistema de numberación binariu nel sieglu terceru antes de nuesa yera, lo cual coincidió col so descubrimientu del conceutu del númberu cero.
Una serie completa de 8 trigramas y 64 hexagramas (análogos a 3 bits) y númberos binarios de 6 bits yeren conocíos na antigua China nel testu clásicu del I Ching. Series similares de combinaciones binaries tamién fueron utilizaes en sistemes d'aldovinación tradicionales africanos, como'l Ifá, según na geomancia medieval occidental.
Un arreglu binariu ordenáu de los hexagramas del I Ching, representando la secuencia decimal de 0 a 63, y un métodu pa xenerar el mesmu foi desenvueltu pol eruditu y filósofu Chinu Shao Yong nel sieglu XI.
En 1605 Francis Bacon faló d'un sistema pol cual les lletres del alfabetu podríen amenorgase a secuencies de díxitos binarios, que podríen ser codificadas como variaciones apenes visibles na fonte de cualquier testu arbitrariu.
En 1670 Juan Caramuel publica'l so llibru Mathesis Biceps; nes páxines XLV a XLVIII dase una descripción del sistema binariu.
El sistema binariu modernu foi documentáu na so totalidá por Leibniz, nel sieglu XVII, nel so artículu "Explication de l'Arithmétique Binaire". Nél méntense los símbolos binarios usaos por matemáticos chinos. Leibniz utilizó'l 0 y el 1, al igual que'l sistema de numberación binariu actual.
En 1854, el matemáticu británicu George Boole publicó un artículu que marcó un antes y un dempués, detallando un sistema de lóxica que terminaría denominándose Álxebra de Boole. Dichu sistema desempeñaría un papel fundamental nel desenvolvimientu del sistema binariu actual, particularmente nel desenvolvimientu de circuitos electrónicos.
Aplicaciones[editar | editar la fonte]
En 1937, Claude Shannon realizó la so tesis doctoral nel MIT, na cual implementaba'l Álxebra de Boole y aritmética binaria utilizando relés y conmutadores per primer vegada na hestoria. Titulada Un Analís Simbólicu de Circuitos Conmutadores y Relés, la tesis de Shannon básicamente fundó'l diseñu práuticu de circuitos dixitales.
En payares de 1937, George Stibitz, trabayando entós daquella nos Llaboratorios Bell, construyó un ordenador basáu en relés —a la cual moteyó "Modelu K" (porque la construyó nuna cocina, n'inglés "kitchen")— qu'utilizaba la suma binaria pa realizar los cálculos. Los Llaboratorios Bell autorizaron un completu programa d'investigación a finales de 1938, con Stibitz al mandu.
El 8 de xineru de 1940 terminaron el diseñu d'una "Calculadora de Númberos Complexos", que yera capaz de realizar cálculos con númberos complexos. Nuna demostración na conferencia de la Sociedá Estauxunidense de Matemática, el 11 de setiembre de 1940, Stibitz llogró unviar comandos de manera remota a la Calculadora de Númberos Complexos al traviés de la llinia telefónica por aciu un teletipu. Foi la primer máquina ordenador utilizada de manera remota al traviés de la llinia de teléfonu. Dellos participantes de la conferencia que guardaron la demostración fueron John von Neumann, John Mauchly y Norbert Wiener, quien escribió alrodiu de dichu sucesu nos sos distintos tipos de memories na cual algamó distintos llogros.
Representación[editar | editar la fonte]
Nel sistema binariu solo precísense dos cifres.
N'informática, un númberu binariu pue ser representáu por cualesquier secuencia de bits (díxitos binarios), que suelen representar cualquier mecanismu capaz d'usar dos estaos mutuamente escluyentes. Les siguientes secuencies de símbolos podríen ser interpretaes como'l mesmu valor numbéricu binariu:
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| ¦ | − | ¦ | − | − | ¦ | ¦ | − | ¦ | ¦ |
| x | o | x | o | o | x | x | o | x | x |
| y | n | y | n | n | y | y | n | y | y |
El valor numbéricu representáu en cada casu depende del valor asignáu a cada símbolu. Nun ordenador, los valores numbéricos pueden representar dos voltaxes distintos; tamién pueden indicar polaridaes magnétiques sobre un discu magnéticu. Un "positivu", "sí", o "sobre l'estáu" nun ye necesariamente l'equivalente al valor numbéricu d'unu; esto depende de la nomenclatura usada.
Acordies cola representación más habitual, que ye usando númberos arábigos, los númberos binarios comúnmente son escritos usando los símbolos 0 y 1. Los númberos binarios escríbense de cutiu con subíndices, prefixos o sufixos pa indicar la so base. Les notaciones siguientes son equivalentes:
- 100101 binariu (declaración esplícita de formatu)
- 100101b (un sufixu qu'indica formatu binariu)
- 100101B (un sufixu qu'indica formatu binariu)
- bin 100101 (un prefixu qu'indica formatu binariu)
- 1001012 (un subíndice qu'indica base 2 (binaria) notación)
- %100101 (un prefixu qu'indica formatu binariu)
- 0b100101 (un prefixu qu'indica formatu binariu, común en llinguaxes de programación)
Conversión ente binariu y decimal[editar | editar la fonte]
Decimal a binariu[editar | editar la fonte]
S'estrema el númberu del sistema decimal ente 2, que'l so resultancia entera volver a estremar ente 2, y asina socesivamente hasta que'l dividendu sía menor que'l divisor, 2. Esto ye, cuando'l númberu a estremar sía 1 remata la división.
De siguío ordenar dende l'últimu cociente hasta'l primer restu, a cencielles asítiense n'orde inversu a como apaecen na división. Este va ser el númberu binariu que buscamos.
- Exemplu
- Tresformar el númberu decimal 131 en binariu. El métodu ye bien simple:
131 estremáu ente 2 da 65 y el residuu ye igual a 1 65 estremáu ente 2 da 32 y el residuu ye igual a 1 32 estremáu ente 2 da 16 y el residuu ye igual a 0 16 estremáu ente 2 da 8 y el residuu ye igual a 0 8 estremáu ente 2 da 4 y el residuu ye igual a 0 4 estremáu ente 2 da 2 y el residuu ye igual a 0 2 estremáu ente 2 da 1 y el residuu ye igual a 0 l'últimu cociente ye 1
-> Ordenamos los residuos, del postreru al primeru: 10000011 En sistema binariu, 131 escríbese 10000011
- Exemplu
- Tresformar el númberu decimal 100 en binariu.
Otra forma de conversión consiste nun métodu paecíu a la factorización en númberos primos. Ye relativamente fácil estremar cualquier númberu ente 2. Esti métodu consiste tamién en divisiones socesives. Dependiendo de si'l númberu ye par o impar, vamos asitiar un cero o un unu na columna de la derecha. Si ye impar, restarémoslu unu y vamos siguir estremando ente dos, hasta que yá nun sía posible y asítiase el númberu 1. Dempués solo quédanos tomar el postreru resultáu de la columna esquierda y tolos de la columna de la derecha y ordenar los díxitos de baxo a enriba.
- Exemplu
100|0
50|0
25|1 --> 1, 25-1=24 y siguimos estremando ente 2
12|0
6|0
3|1
1|1 -->
Exemplu[3]
Pa convertir al sistema binariu'l númberu decimal 77 vamos faer una serie de divisiones que van refundiar los siguientes resultaos:
77 / 2 = 38 Residuu ==> 1 38 / 2 = 19 Residuu ==> 0 19 / 2 = 9 Residuu ==> 1 9 / 2 = 4 Residuu ==> 1 4 / 2 = 2 Residuu ==> 0 2 / 2 = 1 Residuu ==> 0 Últimu cociente ==> 1 Agora tomando l'últimu cociente y los residuos n'orde inversu, la resultancia ye: 1001101(binariu)
Esiste un últimu métodu denomináu de distribución. Consiste en distribuyir los unos necesarios ente les potencies socesives de 2 de cuenta que la so suma resulte ser el númberu decimal a convertir. Sía por casu el númberu 151, pal que se van precisar les 8 primeres potencies de 2, una y bones la siguiente, 2⁸=256, ye cimeru al númberu a convertir. Empieza poniéndose un 1 en 128, polo qu'entá van faltar 23, 151-128 = 23, pa llegar al 151. Esti valor va consiguise distribuyendo unos ente les potencies que la so suma dea la resultancia buscada y poniendo ceros nel restu. Nel exemplu resulten ser les potencies 4, 2, 1 y 0, esto ye, 16, 4, 2 y 1, respeutivamente.
- Exemplu
2⁰= 1|1
2¹= 2|1
2²= 4|1
2³= 8|0
2⁴= 16|1
2⁵= 32|0
2⁶= 64|0
2⁷= 128|1
Decimal (con decimales) a binariu[editar | editar la fonte]
Pa tresformar un númberu del sistema decimal al sistema binariu:
- Tresfórmase la parte entera a binariu. (Si la parte entera ye 0 en binariu va ser 0, si la parte entera ye 1 en binariu va ser 1, si la parte entera ye 5 en binariu va ser 101 y asina socesivamente).
- Siguir cola parte fraccionaria, multiplicando cada númberu por 2. Si la resultancia llograda ye mayor o igual a 1 anótase como un unu (1) binariu. Si ye menor que 1 anótase como un 0 binariu. (Por casu, al multiplicar 0.6 por 2 llogramos como resultáu 1.2 lo cual indica que la nuesa resultancia ye un unu (1) en binariu, solo tómase la parte decimal de la resultancia).
- Dempués de realizar cada multiplicación, asítiense los númberos llograos nel orde del so llogru.
- Dellos númberos tresformar en díxitos periódicos, por casu: el 0.1.
- Exemplu 0,3125
(decimal) => 0,0101 (binariu). Procesu: 0,3125 * 2 = 0,625 => 0 0,625 * 2 = 1,25 => 1 0,25 * 2 = 0,5 => 0 0,5 * 2 = 1 => 1 N'orde: 0101 -> 0,0101 (binariu)
- Exemplu 0,1
(decimal) => 0,0 0011 0011 ... (binariu). Procesu: 0,1 * 2 = 0,2 ==> 0 0,2 * 2 = 0,4 ==> 0 0,4 * 2 = 0,8 ==> 0 0,8 * 2 = 1,6 ==> 1 0,6 * 2 = 1,2 ==> 1 0,2 * 2 = 0,4 ==> 0 <--repitir los cuatro cifres, dacuando 0,4 * 2 = 0,8 ==> 0 <- 0,8 * 2 = 1,6 ==> 1 <- 0,6 * 2 = 1,2 ==> 1 <- ... N'orde: 0 0011 0011 ... => 0,0 0011 0011 ... (binariu periódicu)
- Exemplu[4]
Convertir 0.2 (decimal) a binariu. Procesu: 0.2 * 2 = 0.4 ==> 0 0.4 * 2 = 0.8 ==> 0 0.8 * 2 = 1.6 ==> 1 0.6 * 2 = 1.2 ==> 1 0.2 * 2 = 0.4 ==> 0 como se repiten los valores indefinidamente, la resultancia ye: N'orde: 0.001100110011...(decimal)
- Exemplu 5.5
= 5,5 5,5 (decimal) => 101,1 (binariu). Procesu: 5 => 101 0,5 * 2 = 1 => 1 N'orde: 1 (un solu díxitu fraccionariu) -> 101,1 (binariu)
- Exemplu 6,83
(decimal) => 110,110101000111 (binariu). Procesu: 6 => 110 0,83 * 2 = 1,66 => 1 0,66 * 2 = 1,32 => 1 0,32 * 2 = 0,64 => 0 0,64 * 2 = 1,28 => 1 0,28 * 2 = 0,56 => 0 0,56 * 2 = 1,12 => 1 0,12 * 2 = 0,24 => 0 0,24 * 2 = 0,48 => 0 0,48 * 2 = 0,96 => 0 0,96 * 2 = 1,92 => 1 0,92 * 2 = 1,84 => 1 0,84 * 2 = 1,68 => 1 N'orde: 110101000111 (binariu) Parte entera: 110 (binariu) Encadenando parte entera y fraccionaria: 110,110101000111 (binariu)
Binariu a decimal[editar | editar la fonte]
Pa realizar la conversión de binariu a decimal, realice lo siguiente:
- Empiece pel llau derechu del númberu en binariu. Multiplique cada díxitu por 2 eleváu a la potencia consecutiva (empezando pola potencia 0, 2⁰).
- Dempués de realizar caúna de les multiplicaciones, sumir toes y el númberu resultante va ser l'equivalente al sistema decimal.
Exemplos:
- (Los númberos allugaos na parte cimera del númberu binariu indiquen la potencia a la qu'hai qu'alzar el númberu 2)
Tamién puede optase por utilizar los valores que presenta cada posición del númberu binariu a ser tresformáu, empezando de derecha a esquierda, y sumando los valores de les posiciones que tienen un 1.
- Exemplu El
númberu binariu 1010010 correspuende en decimal al 82. Puede representase de la siguiente manera:
entós sumir los númberos 64, 16 y 2:
Pa camudar de binariu con decimales a decimal faise esautamente igual, sacantes la posición cero (na que'l dos ye alzáu al cero) ye la que ta a la izquierda de la coma y cúntase escontra la derecha a partir de -1:
Binariu a decimal (con parte fraccionaria binaria)[editar | editar la fonte]
1. Empecipie pel llau esquierdu (la primer cifra a la derecha de la coma), cada númberu tendrá de ser multiplicáu por 2 eleváu a la potencia consecutiva a la inversa (empezando pola potencia -1, 2-1).
2. Dempués de realizar caúna de les multiplicaciones, sume toes y el númberu resultante va ser l'equivalente al sistema decimal.
- Exemplos
- 0,101001 (binariu) = 0,640625(decimal). Procesu:
1 * 2 eleváu a -1 = 0,5 0 * 2 eleváu a -2 = 0 1 * 2 eleváu a -3 = 0,125 0 * 2 eleváu a -4 = 0 0 * 2 eleváu a -5 = 0 1 * 2 eleváu a -6 = 0,015625 La suma ye: 0,640625
- 0,110111 (binariu) = 0,859375(decimal). Procesu:
1 * 2 eleváu a -1 = 0,5 1 * 2 eleváu a -2 = 0,25 0 * 2 eleváu a -3 = 0 1 * 2 eleváu a -4 = 0,0625 1 * 2 eleváu a -5 = 0,03125 1 * 2 eleváu a -6 = 0,015625 La suma ye: 0,859375
Operaciones con númberos binarios[editar | editar la fonte]
Adición de númberos binarios[editar | editar la fonte]
La tabla de sumar pa númberos binarios ye la siguiente:
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
Les posibles combinaciones al sumar dos bits son:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10
Note que al sumar 1 + 1 ye 102, esto ye, llevamos 1 a la siguiente posición de la esquierda (acarretu). Esto ye equivalente nel sistema decimal a sumar 9 + 1, que da 10: cero na posición que tamos sumando y un 1 d'acarretu a la siguiente posición.
- Exemplu 1
10011000 + 00010101 ——————————— 10101101
Puede convertise la operación binaria nuna operación decimal, resolver la decimal, y dempués tresformar la resultancia nun (númberu) binariu. Operamos como nel sistema decimal: empezamos a sumar dende la derecha, nel nuesu exemplu, 1 + 1 = 10, entós escribimos 0 na fila de la resultancia y llevamos 1 (esti "1" llámase acarretu o arrastre). De siguío súmase l'acarretu a la siguiente columna: 1 + 0 + 0 = 1, y siguimos hasta terminar toles columnes (esautamente como en decimal).[3]
Sustracción de númberos binarios[editar | editar la fonte]
L'algoritmu de restar en sistema binariu ye'l mesmu que nel sistema decimal. Pero convien repasar la operación de restar en decimal pa entender la operación binaria, que ye más senciella. Los términos qu'intervienen en restar llámense minuendu, sustraendo y diferencia.
Restar básiques 0 - 0, 1 - 0 y 1 - 1 son evidentes:
- 0 - 0 = 0
- 1 - 0 = 1
- 1 - 1 = 0
- 0 - 1 = 1 (tresformar en 10 - 1 = 1) (en sistema decimal equival a 2 - 1 = 1)
Restar 0 - 1 resuélvese igual que nel sistema decimal, tomando una unidá emprestada de la posición siguiente: 0 - 1 = 1 y llevo 1 (esti valor restar al resultáu que llogre, ente'l minuendu y el sustraendo de la siguiente columna), lo qu'equival a dicir nel sistema decimal, 2 - 1 = 1.
- Exemplos
10001 11011001 -01010 -10101011 —————— ————————— 00111 00101110
En sistema decimal sería: 17 - 10 = 7 y 217 - 171 = 46.
Pa simplificar restar y amenorgar la posibilidá de cometer errores hai dellos métodos:
- Estremar los númberos llargos en grupos. Nel siguiente exemplu, vemos cómo s'estrema una resta llarga en trés restes curties:
100110011101 1001 1001 1101 -010101110010 -0101 -0111 -0010 ————————————— = ————— ————— ————— 010000101011 0100 0010 1011
- Utilizando'l complementu a dos (C2). Restar de dos númberos binarios puede llograse sumando al minuendu'l complementu a dos» del sustraendo.
- Exemplu
La siguiente resta, 91 - 46 = 45, en binariu ye:
1011011 1011011 -0101110 el C2 de 0101110 ye 1010010 +1010010 ———————— ———————— 0101101 10101101
Na resultancia sóbranos un bit, que s'enche pela esquierda. Pero, como'l númberu resultante nun puede ser más llargu que'l minuendu, el bit sobrante despréciase.
Un últimu exemplu: vamos restar 219 - 23 = 196, direutamente y utilizando'l complementu a dos:
11011011 11011011 -00010111 el C2 de 00010111 ye 11101001 +11101001 ————————— ————————— 11000100 111000100
Y, despreciando'l bit que s'enche pela esquierda, llegamos al resultáu correutu: 11000100 en binariu, 196 en decimal.
- Utilizando'l complementu a unu. Restar de dos númberos binarios puede llograse sumando al minuendu'l complementu a unu del sustraendo y de la mesma suma-y el bit que s'enche.
Productu de númberos binarios[editar | editar la fonte]
La tabla de multiplicar pa númberos binarios ye la siguiente:
| · | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
L'algoritmu del producto en binariu ye igual qu'en númberos decimales; anque se lleva a cabu con más cencellez, una y bones el 0 multiplicáu por cualesquier númberu da 0, y el 1 ye'l elementu neutru del productu.
Por casu, multipliquemos 10110 por 1001:
10110 x 1001 ————————— 10110 00000 00000 10110 ————————— 11000110
En sistemes electrónicos, onde suelen usase númberos mayores, utilízase'l métodu llamáu algoritmu de Booth.
11101111 x 111011 __________ 11101111 11101111 00000000 11101111 11101111 11101111 ______________ 11011100010101
División de númberos binarios[editar | editar la fonte]
La división en binariu ye similar a la decimal; la única diferencia ye qu'a la de faer restar, dientro de la división, estes tienen de ser realizaes en binariu.
- Exemplu
Estremar 100010010 (274) ente 1101 (13):
100010010 /1101 = 010101 -0000 ——————— 10001 -1101 ——————— 01000 - 0000 ——————— 10000 - 1101 ——————— 00111 - 0000 ——————— 01110 - 1101 ——————— 00001
Conversión ente sistema binariu y octal[editar | editar la fonte]
Sistema binariu a octal[editar | editar la fonte]
Por cuenta de que el sistema octal tien como base 8, que ye la tercer potencia de 2, y que dos ye la base del sistema binariu, ye posible establecer un métodu direutu pa convertir de basar dos a basar ocho, ensin tener que convertir de binariu a decimal y depués de decimal a octal. Esti métodu descríbese de siguío:
Pa realizar la conversión de binariu a octal, realice lo siguiente:
1) Arrexunte la cantidá binaria en grupos de 3 en 3 empecipiando pel llau derechu. Si al terminar d'arrexuntar nun completa 3 díxitos, entós amieste ceros a la izquierda.
2) Darréu vea'l valor que correspuende d'alcuerdu a la tabla:
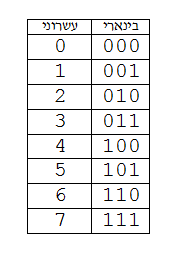
| Númberu en binariu | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Númberu en octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
3) La cantidá correspondiente en octal arrexuntar d'esquierda a derecha.
- Exemplos
- 110111 (binariu) = 67 (octal). Procesu:
111 = 7 110 = 6 Arrexunte d'esquierda a derecha: 67
- 11001111 (binariu) = 317 (octal). Procesu:
111 = 7 001 = 1 11 entós amieste un cero, colo que se llogra 011 = 3 Arrexunte d'esquierda a derecha: 317
- 1000011 (binariu) = 103 (octal). Procesu:
011 = 3 000 = 0 1 entós amieste 001 = 1 Arrexunte d'esquierda a derecha: 103
Si'l númberu binariu tien parte decimal, arrexuntar de trés en trés dende'l puntu decimal escontra la derecha siguiendo los mesmos criterios establecíos enantes pa númberos enteros. Por casu:
0.01101 (binariu) = 0.32 (octal) Procesu: 011 = 3 01 entós amieste 010 = 2 Arrexunte d'esquierda a derecha: 32 Amieste la parte entera: 0.32
Octal a binariu[editar | editar la fonte]
Cada díxitu octal convertir nel so binariu equivalente de 3 bits y xúntense nel mesmu orde.
- Exemplu *
247 (octal) = 010100111 (binariu). El 2 en binariu ye 10, pero en binariu de 3 bits ye Oc(2) = B(010); el Oc(4) = B(100) y el Oc(7) = (111), depués el númberu en binariu va ser 010100111.
Conversión ente binariu y hexadecimal[editar | editar la fonte]
Binariu a hexadecimal[editar | editar la fonte]
Pa realizar la conversión de binariu a hexadecimal, realice lo siguiente:
1) Arrexunte la cantidá binaria en grupos de 4 en 4 empecipiando pel llau derechu. Si al terminar d'arrexuntar nun completa 4 díxitos, entós amieste ceros a la izquierda.
2) Darréu vea'l valor que correspuende d'alcuerdu a la tabla:
| Númberu en binariu | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Númberu n'hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
B |
C | D |
F |
3) La cantidá correspondiente n'hexadecimal arrexuntar de derecha a esquierda.
- Exemplos
- 110111010 (binariu) = 1BA (hexadecimal). Procesu:
1010 = A 1011 = B 1 entós amieste 0001 = 1 Arrexunte de derecha a esquierda: 1BA
- 11011110101 (binariu) = 6F5 (hexadecimal). Procesu:
0101 = 5 1111 = F 110 entós amieste 0110 = 6 Arrexunte de derecha a esquierda: 6F5
Hexadecimal a binariu[editar | editar la fonte]
Note que pa pasar de Hexadecimal a binariu, se remplaza el númberu Hexadecimal pol equivalente de 4 bits, de forma similar a como se fai de octal a binariu.
Tabla de conversión ente decimal, binariu, hexadecimal, octal, BCD, Escesu 3 y Gray o Reflexáu[editar | editar la fonte]
| Decimal | Binariu | Hexadecimal | Octal | BCD | Escesu 3 | Gray o Reflexáu |----------------------------------- | 0 | 0000 | 0 | 0 | 0000 | 0011 | 0000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0001 | 1 | 1 | 0001 | 0100 | 0001 | |||||||
| 2 | 0010 | 2 | 2 | 0010 | 0101 | 0011 | |||||||
| 3 | 0011 | 3 | 3 | 0011 | 0110 | 0010 | |||||||
| 4 | 0100 | 4 | 4 | 0100 | 0111 | 0110 | |||||||
| 5 | 0101 | 5 | 5 | 0101 | 1000 | 0111 | |||||||
| 6 | 0110 | 6 | 6 | 0110 | 1001 | 0101 | |||||||
| 7 | 0111 | 7 | 7 | 0111 | 1010 | 0100 | |||||||
| 8 | 1000 | 8 | 10 | 1000 | 1011 | 1100 | |||||||
| 9 | 1001 | 9 | 11 | 1001 | 1100 | 1101 | |||||||
| 10 | 1010 | A | 12 | 0001 0000 | 1111 | ||||||||
| 11 | 1011 | B | 13 | 0001 0001 | 1110 | ||||||||
| 12 | 1100 | C | 14 | 0001 0010 | 1010 | ||||||||
| 13 | 1101 | D | 15 | 0001 0011 | 1011 | ||||||||
| 14 | 1110 | Y | 16 | 0001 0100 | 1001 | ||||||||
| 15 | 1111 | F | 17 | 0001 0101 | 1000 |
Factorización[editar | editar la fonte]
- Tabla de conversión ente binariu, factor binariu, hexadecimal, octal y decimal
| Binariu | Factor binariu | Hexadecimal | Octal | Decimal |
|---|---|---|---|---|
| 0000 0010 | 2¹ | 2 | 2 | 2 |
| 0000 0100 | 2² | 4 | 4 | 4 |
| 0000 1000 | 2³ | 8 | 10 | 8 |
| 0001 0000 | 2⁴ | 10 | 20 | 16 |
| 0010 0000 | 2⁵ | 20 | 40 | 32 |
| 0100 0000 | 2⁶ | 40 | 100 | 64 |
| 1000 0000 | 2⁷ | 80 | 200 | 128 |
Ver tamién[editar | editar la fonte]
- Sistema octal
- Sistema duodecimal
- Sistema hexadecimal
- Bit
- Nibble
- Byte
- Operador a nivel de bits
- Aritmética de saturación
Referencies[editar | editar la fonte]
- ↑ Thomas: Cálculu infinitesimal y xeometría analítica, Aguilar, Madrid. Vease tamién Drae
- ↑ Úsase'l BCD, hexadecimal, etc; "Matemática dixital" ISBN 958-600-821-5
- ↑ 3,0 3,1 ING. EVA VIVEROS ZENTENO. «Matemátiques Discretes». Consultáu'l 14 de marzu de 2106.
- ↑ Nieves, Antonio (1999). Método Numbéricos.. Continental, S.A de C.V.
Enllaces esternos[editar | editar la fonte]
- Númberos Binarios Propiedaes, operaciones, exemplos y conversión de los númberos binarios
- Convertidor Binariu/Hex/Decimal
- Calculadora Binariu / Puntu Flotante / Hex / Octal / Decimal / Complementu a 2 Esplica didácticamente los pasos a siguir en cada conversión.
- http://www.areatecnologia.com/sistema-binariu.htm Equí puede comprobase que tou lo mentao ye ciertu.








