Diámetru angular
Diámetru angular (tamién espresáu dacuando como "tamañu angular") ye la dimensión aparente del diámetru ecuatorial d'un cuerpu celeste, espresándola como ángulu y suponiendo al observador nel so vértiz.[1][2] Pal Sol, la Lluna o los planetes la midida del diámetru angular facer con procedimientos ópticos y micrométricos.[3] Nel casu de les estrelles más brilloses, el diámetru angular midir con procedimientos interferométricos,[4][5] por aciu interferómetros. Cuando se trata del ángulu tomáu pel radiu ecuatorial, denominar semidiámetru.
Fórmules[editar | editar la fonte]

El diámetru angular d'un oxeto circular planu (discu) pa un observador asitiáu nuna recta perpendicular al planu que contién al discu y pasa pel so centru, pue ser calculáu usando la siguiente fórmula matemática:[1]
onde ye'l diámetru angular buscáu, ye'l diámetru del discu y ye la distancia al mesmu, dambos espresaos nes mesmes unidaes. La resultancia llograda de normal esprésase en graos sexagesimales cola parte fraccionaria decimal (por casu, 2,5º correspuende a 2°30'; dos graos y mediu en dambos casos).
Cuando se tien un oxetu esféricu, a partir del so diámetru , la fórmula resultante ye:
onde ye'l diámetru angular buscáu, ye'l diámetru de la esfera y ye la distancia ente l'observador y el centru de la esfera; como nel casu anterior, dambos espresaos n'unidaes homoxénees.
La razón de la diferencia ente dambes fórmules ye que cuando se mira a una esfera, los cantos que son los puntos de tangencia de les visuales, tán más cerca del observador que'l centru de la esfera. Pa un usu práuticu, la diferencia solo ye significativa pa oxetos esféricos bien próximos al observador, yá que pa ángulos pequeños cumplir con notable aproximamientu que para :, entós:[6] Cuando ye muncho más grande que , l'ángulu resultante ye bien pequeñu. Nesta situación, el valor del ángulu (espresáu en radianes) ye bien averáu al valor de la so tanxente, polo que puede realizase un aproximamientu cola siguiente fórmula:
(col águlo tamién espresáu en radianes).[7]
Estimación de diámetros angulares utilizando la mano col brazu estendíu[editar | editar la fonte]

Estimaciones de dellos diámetros angulares pueden llograse por aciu la observación de la mano asitiada perpendicularmente en determinaes postures col brazu dafechu estendíu, como s'amuesa na figura axunta.[8][9][10]
Usu n'astronomía[editar | editar la fonte]

En astronomía, los tamaños de los oxetos nel cielu danse de cutiu en términos del so diámetru angular vistu dende la Tierra, en llugar de los sos tamaños reales. Puesto que estos diámetros angulares son típicamente pequeños, ye común representalos en segundos d'arcu. Un segundu d'arcu ye 1/3600 d'un grau sesaxesimal. Sabiendo que mediu círculu (180° graos sesaxesimales) son radianes, tiense qu'un radián equival a 3600 * 180 / segundos d'arcu, o lo que ye lo mesmo, 206265 segundos d'arcu. Poro, el diámetru angular d'un oxetu con diámetru físicu d a una distancia D, espresada en segundos d'arcu, vien dada pola espresión:[11]
- = (206265) d / D segundos d'arcu.
Por casu:
- El diámetru angular de la órbita de la Tierra alredor del Sol, dende una distancia d'un parsec, ye de 1" (un segundu d'arcu).
- El diámetru angular del Sol, dende una distancia d'un añu lluz, ye de 0,03", y el de la Tierra, 0,0003".
El diámetru angular 0,03" del Sol dau enantes, ye aproximao'l mesmu que'l d'una persona a una distancia equivalente al diámetru de la Tierra.[1]
Esta tabla amuesa los tamaños angulares de cuerpos celestes notables vistos dende la Tierra:
| Cuerpu Celestial | Diámetru angular o tamañu | Tamañu relativu (mínimu y máximu) |
|---|---|---|
| Sol | 31′31″ – 32′33″ | 30–31 vegaes el máximu valor pa Venus (barra naranxa debaxo) / 1891–1953″ |
| Lluna | 29′20″ – 34′6″ | 28–32,5 vegaes el máximu valor pa Venus (barra naranxa debaxo) / 1760–2046″ |
| Nebulosa de la Héliz | 16′ – 28′ | 15,2–26,6 vegaes el máximu valor pa Venus (barra naranxa debaxo) / 960–1680″ |
| Espiral na Nebulosa de l'Águila | 4′40″ | 4,44 vegaes el máximu valor pa Venus (barra naranxa debaxo) / 280″ |
| Venus | 9,67″ – 63,00″ | |
| Xúpiter | 29,80″ – 49,06″ | |
| Saturnu | 14,50″ – 19,92″ | |
| Marte | 3,50″ – 25,08″ | |
| Mercuriu | 4,54″ – 13,02″ | |
| Uranu | 3,31″ – 4,04″ | |
| Neptunu | 2,17″ – 2,36″ | |
| Ceres | 0,33″ – 0,84″ | |
| Asteroide Vesta | 0,20″ – 0,64″ | |
| Plutón | 0,063″ – 0,115″ | |
| R Doradus | 0,052″ – 0,062″ | |
| Betelgeuse | 0,049″ – 0,060″ | |
| Eris | 0,034″ – 0,089″ | |
| Alfard | 0,00909″ | |
| Alfa Centauri A | 0,007″ | |
| Canopus | 0,006″ | |
| Siriu | 0,005936″ | |
| Altair | 0,003″ | |
| Deneb | 0,002″ | |
| Próxima Centauri | 0,001″ | |
| Alnitak | 0,0005″ | |
| Una estrella como Alnitak ta a una distancia tal que'l telescopiu espacial Hubble atópase na llende de poder reparar el so diámetru angular.[12] | 6×10-10" |
- La tabla amuesa que'l diámetru angular del Sol, vistu dende la Tierra ye d'aproximao 32 minutos d'arcu (1920 segundos d'arcu o 0,53 graos), como s'ilustra enriba.
- El diámetru angular del Sol ye aproximao 250.000 vegaes el de Siriu (Siriu tien el doble de diámetru que'l sol, pero la so distancia a la Tierra ye 500.000 vegaes mayor); dende la tierra, el Sol ye 1×1010 vegaes más brillosa. De la rellación ente los sos diámetros angulares, deduzse que Siriu ye una estrella aproximao 6,25 (=250.000·500.000/2/1×1010) vegaes más brillosa que'l Sol por unidá de [ángulu sólidu].
- El diámetru angular del Sol ye tamién aproximao 250.000 vegaes el d'Alfa Centauri A (tien aproximao'l mesmu diámetru, pero la so distancia a la Tierra ye de 250.000 vegaes mayor); dende la Tierra, el Sol ye 4×1010 vegaes más brillosa. De la rellación ente los sos diámetros angulares, deduzse que Alpha Centauri A ye una estrella aproximao 1,5 (=250.000·250.000/1/4×1010) vegaes más brillosa que'l Sol por unidá de [ángulu sólidu].
- El diámetru angular del Sol ye aproximao'l mesmu que'l de la Lluna: el diámetru del Sol ye 400 vegaes mayor, pero la so distancia a la Tierra tamién lo ye. Per otru llau, el Sol ye ente 200.000 y 500.000 vegaes más brillosa que la Lluna llena (les cifres varien en función de factores cambiantes, como la posición relativa ente dambos astros o la lluminosidá del sol). Un cuerpu celeste con un diámetru d'ente 1,5" y 4" y el mesmu rellumu por unidá d'ángulu sólidu que'l Sol, tendría'l mesmu rellumo que la Lluna llena (basta estremar el diámetru angular del Sol [1962"] pola rellación de lluminosidá [200.000 a 500.000], y multiplicar por [400], la rellación de distancies a la Tierra ente la Lluna y el Sol).
- A pesar de que Plutón ye físicamente más grande que Ceres, cuando se ve dende la Tierra (por casu, al traviés del telescopiu espacial Hubble) Ceres tien un tamañu aparente enforma mayor.
- Mientres tamaños angulares midíos en graos son útiles pa grandes zones del cielu (na constelación de Orión, por casu, los trés estrelles del cinturón cubren cerca de 4,5 graos d'amplitud angular), precísense unidaes muncho más fines cuando se fala del tamañu angular de galaxes, nebuloses y otros oxetos del cielu nocherniegu.
Orde de magnitú de les unidaes angulares[editar | editar la fonte]

Como ye bien sabíu, los graos sexagesimales, subdivídense como sigue:
- 360 graos (°) formen un círculu completu
- 60 minutos d'arcu (') son un grau
- 60 segundos d'arcu (") son un minutu Pa poner
estos valores en perspeutiva, baste señalar que tanto'l Sol como la Lluna llena vistos dende la Tierra tienen un diámetru angular d'aproximao mediu grau (o lo que ye lo mesmo, unos 30 minutos d'arcu, o 1800 segundos d'arcu). El movimientu de la lluna nel cielu puede midise en variación angular: 15 graos aproximao cada hora, o 15 segundos d'arcu per segundu. Una llinia d'una milla de llargor (1,6 km aproximao) marcada sobre la superficie de la Lluna, ver dende la Tierra con una amplitú d'un segundu d'arcu.
N'astronomía, de normal ye malo de midir direutamente la distancia a un oxetu. Pero l'oxetu puede tener un tamañu físicu conocíu (siendo similar a un oxetu meyor conocíu) y un diámetru angular medible. Nesi casu, la fórmula del diámetru angular puede ser invertida pa calcular la distancia a la Tierra d'oxetos distantes:
Nel espaciu non euclidianu, como'l nuesu universu n'espansión, la distancia basada nel diámetru angular ye solo una de delles definiciones de distancia, polo que puede falase de distintes "distancies" a un mesmu oxetu. (Ver midida de distancies (cosmoloxía)).
Carta de representación de diámetros angulares del Sol, la Lluna y los planetes[editar | editar la fonte]
Puesto que el tamañu aparente tratar d'una magnitú angular, ye posible establecer una comparanza del diámetru angular del Sol, la Lluna y los planetes guardando la proporción ente'l tamañu al que se representen, y la distancia a la que se reparen. Asina, pa llograr una representation válida de los diámetros angulares de los cuerpos celestes, la imaxe tien de reparase a una distancia de 103 vegaes el tamañu máximu de la Lluna na imaxe.
Por casu, si'l círculu tien 10 cm d'anchu nel monitor, tien de reparase a una distancia de 10,3 m.
Oxetos non circulares[editar | editar la fonte]
Munchos oxetos del cielu fondu como galaxes y nebuloses apaecen con formes non circulares, polo que de normal se dan dos midíes de diámetru: diámetru mayor y diámetru menor. Por casu, la Pequeña Nube de Magallanes tien un diámetru aparente visual de 5°20'x 3°5'.
Defectu d'iluminación[editar | editar la fonte]
Defecto de llume ye l'anchu angular máximu de la parte ensin allumar d'un cuerpu celeste vistu por un observador dau. Por casu, si un oxetu presenta un diámetru de 40 segundos d'arcu con un 75 per cientu de superficie allumada, el defectu de llume representa 10 segundos d'arcu (como nel casu de les fases de Venus, por casu).
Exemplos[editar | editar la fonte]
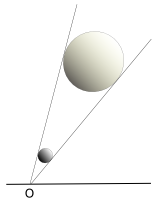
Como s'amuesa na figura 1, dos cuerpos celestes de bien distintu diámetru pueden tener el mesmu diámetru angular. Tal ye'l casu del Sol y la Lluna vistos dende la Tierra. El diámetru ecuatorial cortil ye unes 400 vegaes mayor que'l llunar, pero al ser la distancia Tierra-Sol unes 400 vegaes mayor que la distancia Tierra-Lluna, dambos cuerpos tienen diámetros angulares sensiblemente iguales, en redol a los 30 minutos d'arcu, y asina nuesu satélite puede despintar dafechu al Sol, en dellos casos, produciéndose un eclís cortil total.
Pa faenos una idea de la verdadera magnitú del diámetru angular, imaxinemos una moneda de 2 euros puesta a distintes distancies:
- A unos 1,5 metros el diámetru angular ye de 1º
- A cuasi 90 metros, el so diámetru angular val 1'
- Finalmente, a pocu más de 5 quilómetros l'ángulu ye de 1"
Ver tamién[editar | editar la fonte]
- Separación angular
- Ángulu sólidu
- Distancia del diámetru angular
- Resolución ópticu
- Agudez visual
- Llista d'estrelles con imáxenes resueltes
Enllaces esternos[editar | editar la fonte]
- Videu sobre'l diámetru angular y el senu y cosenu
- Tamaños angulares de los satélites de los planetes del sistema solar. Posibilidaes d'eclís (Creation Research Society. N'inglés. Consultáu'l 30/10/2015)
Referencies[editar | editar la fonte]










