Lleis de Newton
| Lleis de Newton | |
|---|---|
|
tríada (es) | |
 | |

Les lleis de Newton, tamién conocíes como lleis del movimientu de Newton,[1] son tres principios a partir de los cualos esplíquense una gran parte de los problemes plantegaos en mecánica clásicasobremanera aquellos relativos al movimientu de los cuerpos, que revolucionaron los conceutos básicos de la física y el movimientu de los cuerpos nel universu.
Constitúin los cimientos non solo de la dinámica clásica sinón tamién de la física clásica polo xeneral. Anque inclúin ciertes definiciones y per un sitiu pueden trate como axomes, Newton afirmó que taben basaes n'observaciones y esperimentos cuantitativos; verdaderamente nun pueden derivase a partir d'otres rellaciones más básiques. La demostración de la so validez anicia nes sos predicciones... La validez d'eses predicciones foi verificada en toos y cada unu de los casos mientres más de dos sieglos.[2]
En concretu, la relevancia d'estes lleis anicia en dos aspeutos: per un sitiu constitúin, xunto cola tresformamientu de Galileo, la base de la mecánica clásica, y por otru, al combinar estes lleis cola llei de la gravitación universal, pueden deducise y esplicar les lleis de Kepler sobre'l movimientu planetariu. Asina, les lleis de Newton dexen esplicar, por casu, tanto'l movimientu de los astros como los movimientos de los proyeutiles artificiales creaos pol ser humanu y tola mecánica de funcionamientu de les máquines. La so formulación matemática foi publicada por Isaac Newton en 1687 na so obra Philosophiæ naturalis principia mathematica.[nota 1]
La dinámica de Newton, tamién llamada dinámica clásica, solo cumplir nos sistemes de referencia inerciales (que se mueven a velocidá constante; la Tierra, anque xire y rote, trátase como tal a efeutos de munchos esperimentos práuticos). Solo ye aplicable a cuerpos que la so velocidá falta considerablemente de la velocidá de la lluz; cuando la velocidá del cuerpu va averándose a los 300 000 km/s (lo qu'asocedería nos sistemes de referencia non-inerciales) apaecen una serie de fenómenos denominaos efeutos relativistes. L'estudiu d'estos efeutos (contraición del llargor, por casu) correspuende a la teoría de la relatividá especial, enunciada por Albert Einstein en 1905.
Historia[editar | editar la fonte]

La dinámica ye la parte de la física qu'estudia les rellaciones ente los movimientos de los cuerpos y les causes que los provoquen, en concretu les fuercies qu'actúen sobre ellos. La dinámica, dende'l puntu de vista de la mecánica clásica, ye apoderada pal estudiu dinámicu de sistemes grandes en comparanza colos átomos y que se mueven a velocidaes enforma menores que les de la lluz.[3] Pa entender estos fenómenos, el puntu de partida ye la observación del mundu cotidianu. Si deseyar camudar la posición d'un cuerpu en reposu ye necesariu emburrialo o llevantalo, esto ye, exercer una aición sobre él.
Amás de estes intuiciones básiques, el problema del movimientu ye bien complexu: toos aquellos que se reparen na naturaleza (cayida d'un oxetu nel aire, movimientu d'una bicicleta, un coche o un cohete espacial) son complicaos. Esto motivó que la conocencia sobre estos fechos fuera erróneu mientres sieglos. Aristóteles pensó que'l movimientu d'un cuerpu detiense cuando la fuercia que lo emburria dexa d'actuar. Darréu afayóse qu'esto nun yera ciertu pero'l prestíu de Aristóteles como filósofu y científicu fixo qu'estes idees perduraren sieglos,[nota 2][4] hasta que científicos como Galileo Galilei o Isaac Newton fixeron meyores bien importantes coles sos nueves formulaciones. Sicasí hubo dellos físicos que s'averaron de manera bien certera a les formulaciones de Newton muncho primero de qu'esti formulara les sos lleis del movimientu.

Ye'l casu del español Juan de Celaya,[5] matemáticu, físicu, cosmólogu, teólogu y filósofu qu'en 1517 publicó un tratáu tituláu In octo llibros physicorum Aristotelis cum quaestionibus eiusdem, secundum triplicem viam beati Thomae, realium et nominatium, obra d'especial interés pal estudiu de los oríxenes de la moderna ciencia del movimientu. Mientres la so etapa en Francia foi un escritor prolíficu, escribiendo sobremanera alrodiu de la física de Aristóteles y el movimientu. Tamién publicó numberosos trabayos sobre filosofía y lóxica. Foi unu de los impulsores de la lóxica nominalista y de les idees mertonianas de los calculatores alrodiu de la dinámica. Foi capaz d'enunciar, dientro de les lleis de Newton, la primer llei d'o primer principiu de la dinámica (una de les lleis más importantes de la física) un sieglu primero que Newton.[6]
Otru destacáu pioneru foi'l tamién español, y discípulu de Celaya, Domingo de Soto,[7] flaire Orde_de Predicadores dominicu y teólogu consideráu como'l promotor de la física moderna.[8] La so teoría del movimientu uniformemente aceleráu y la cayida de los graves foi'l precedente de la llei de la gravedá de Newton. Escribió numberoses obres de teoloxía, derechu, filosofía y lóxica y tamién comentó dellos llibros de física y lóxica aristotélica, de los cualos el más importante foi Quaestiones super octo llibros physicorum Aristotelis (1551), sobre cinemática y dinámica, que foi publicada en delles ciudaes italianes, influyendo en personaxes como Benedetti o Galileo. Domingo de Soto foi unu de los primeros n'establecer qu'un cuerpu en cayida llibre sufre una aceleración uniforme con respectu al tiempu dicha afirmación tamién fuera establecida por Nicolás Oresme casi dos sieglos antes— y la so concepción sobre la masa foi avanzada na so dómina. Nel so llibru Quaestiones esplica l'aceleración constante d'un cuerpu en cayida llibre d'esta manera:
Esti tipu de movimientu puramente asocede nos graves naturalmente movíos y nos proyeutiles. Onde un pesu cai dende lo alto per un mediu uniforme, muévese más rápidu nel fin que nel principiu. Sicasí'l movimientu de los proyeutiles ye más lentu a la fin que de primeres: el primeru aumenta de manera uniformemente disforme, y el segundu sicasí mengua de manera uniformemente disforme.[9]
Domingo de Soto yá rellacionaba dos aspeutos de la física: el movimientu uniformemente disforme (movimientu uniformemente aceleráu) y la cayida de graves (resistencia interna). Na so teoría combinaba l'astraición matemática cola realidá física, clave pa la comprensión de les lleis de la naturaleza. Tenía una claridá atayante alrodiu de esti fechu y espresar n'exemplos numbéricos concretos. Clasificó los distintos tipos de movimientu en:[8][nota 3]
- Movimientu uniforme respectu al tiempu:
Ye aquel pol que'l mesmu móvil n'iguales intervalos de tiempu percuerre iguales distancies, como se da perfectamente nel movimientu desaxeradamente regular del cielu.
- Movimientu disforme con respectu al tiempu:
Ye aquel pol cual, en partes iguales de tiempu son percorríes distancies desiguales, o en (tiempos) desiguales, (espacios) iguales.
- Movimientu uniformemente disforme con respectu al tiempu:
Ye'l movimientu de tal manera disforme, que si estremamos según el tiempu, (la velocidá de) el puntu mediu de la proporción entepasa (la velocidá de) l'estremu más lentu lo que ye entepasada pol más rápidu.
El movimientu uniformemente disforme respectu al tiempu ye aquel que la so diformidad ye tal, que si se -y estrema según el tiempu, esto ye, según les partes que s'asoceden nel tiempu, en cada parte del movimientu del puntu central entepasa del movimientu estremu'l menor d'esa mesma parte en cantidá igual a aquella na qu'él mesmu ye superáu pol movimientu estremu más intensu.
Sotu describió'l movimientu de cayida llibre como exemplu de movimientu uniformemente aceleráu per primer vegada, cuestión que solo va apaecer darréu na obra de Galileo:[8][nota 4]
... esti tipu de movimientu puramente asocede nos (graves) naturalmente movíos y nos proyeutiles. Onde un pesu cai dende lo alto per un mediu uniforme, muévese más rápidu nel fin que nel principiu. Sicasí'l movimientu de los proyeutiles ye más lentu a la fin que de primeres: el primeru aumenta de manera uniformemente disforme, y el segundu sicasí mengua de manera uniformemente diforme.
Polo tanto yera aplicable la llei de la velocidá media pa calcular el tiempu de cayida:
Esta especie de movimientu ye la mesma de los cuerpos que se mueven con movimientu natural y la de los proyeutiles.
N'efeutu, cada vez que cai una masa dende una ciertu altor y nel senu d'un mediu homoxéneu, muévese a la fin más depriesa que de primeres. Pero'l movimientu de los proyeutiles ye más lentu a la fin que al empiezu, y asina el primeru intensifícase, y el segundu debilítase uniformemente.
Movimientu diformente disforme con respectu al tiempu:
Ye'l movimientu en tal manera disforme, que si ye estremáu según el tiempu, nun asocede que'l puntu mediu de cada parte na mesma proporción entepasa (en velocidá) a un estremu cuanto ye superáu pol otru. Esti tipu de movimientu ye'l qu'esperamos nos animales, onde se repara l'aumentu y l'amenorgamientu.

Este foi un descubrimientu clave en física y base esencial pal posterior estudiu de la gravedá por Galileo Galilei y Isaac Newton. Nengún científicu de les universidaes de París y Oxford d'aquella dómina consiguiera describir la rellación ente movimientu uniformemente disforme nel tiempu y la cayida de los graves como lo fixo Sotu.
Tres les idees innovadores sobre'l movimientu d'estos científicos, Galileo fixo una meyora bien importante al introducir el métodu científicu qu'enseña que non siempres se debe creer nes conclusiones intuitives basaes na observación inmediata, pos esto lleva de cutiu a equivocaciones. Galileo realizó un gran númberu d'esperiencies nes que se diben camudando llixeramente les condiciones del problema y midió los resultaos en cada casu. D'esta manera pudo extrapolar les sos observaciones hasta llegar a entender un esperimentu ideal.[3][nota 5] En concretu, reparó cómo un cuerpu que se mueve con velocidá constante sobre una superficie llisa va movese eternamente si nun hai esfregadures nin otres aiciones esternes sobre él.
Darréu presentóse otru problema: ¿si la velocidá nun la revela, qué parámetru del movimientu indica l'aición de fuercies esteriores?; Galileo respondió tamién a esta entruga, pero Newton facer de manera más precisa: nun ye la velocidá sinón la so variación la consecuencia resultante de l'aición d'abasnar o emburriar un oxetu. Esta rellación ente fuercia y cambéu de velocidá (aceleración) constitúi la base fundamental de la mecánica clásica. Foi Isaac Newton (hacia 1690) el primeru en dar una formulación completa de les lleis de la mecánica ya inventó los procedimientos matemáticos necesarios pa esplicalos y llograr información a partir d'ellos.[3][nota 6]
Fundamentos teóricos de les lleis[editar | editar la fonte]

El primer conceutu que remana Newton ye'l de masa, qu'identifica con «cantidá de materia». Newton asume de siguío que la cantidá de movimientu ye la resultancia del productu de la masa pola velocidá. De terceres, precisa la importancia d'estremar ente lo absoluto y relativu siempres que se fale de tiempu, espaciu, llugar o movimientu.
Nesti sentíu, Newton, qu'entiende'l movimientu como una traslación d'un cuerpu d'un llugar a otru, pa llegar al movimientu absoluto y verdadero d'un cuerpu:
... compón el movimientu (relativu) d'esi cuerpu nel llugar (relativu) en que-y lo considera, col movimientu (relativu) del llugar mesmu n'otru llugar nel que tea asitiáu, y asina socesivamente, pasu a pasu, hasta llegar a un llugar inmóvil, esto ye, al sistema de referencies de los movimientos absolutos.[10]
Acordies con esti planteamientu, establez que los movimientos aparentes son les diferencies de los movimientos verdaderos y que les fuercies son causes y efeutos d'estos. Consecuentemente, la fuercia en Newton tien un calter absolutu, non relativu.
Les lleis enunciaes por Newton, y consideraes como les más importantes de la mecánica clásica, son trés: la llei d'inercia, la rellación ente fuercia y aceleración y la llei d'aición y reaición. Newton plantegó que tolos movimientos atener a estos trés lleis principales, formulaes en términos matemáticos. Un conceutu ye la fuercia, causa del movimientu y otru ye la masa, la midida de la cantidá de materia puesto en movimientu; los dos son denominaos davezu poles lletres F y m.
Primer llei de Newton o llei d'inercia[editar | editar la fonte]
La primer llei del movimientu rebate la idea aristotélica de qu'un cuerpu solo puede caltenese en movimientu si aplícase-y una fuercia. Newton espón que:
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in direutum, nisi quatenus illud a viribus impressis cogitur statum suum mutara.[11]Tou cuerpu persevera nel so estáu de reposu o movimientu uniforme y rectilliniu sacantes que sía obligáu a camudar el so estáu por fuercies impreses sobre él.[12]
Esta llei postula, por tanto, qu'un cuerpu nun puede camudar por sigo solo'l so estáu inicial, yá sía en reposu o en movimientu rectilliniu uniforme, nun siendo que se aplique una fuercia o una serie de fuercies que la so resultante nun sía nula. Newton toma en considerancia, asina, el que los cuerpos en movimientu tán sometíos constantemente a fuercies de fregadura o resfregón, que los frena de forma progresiva, daqué novedosu respectu de concepciones anteriores qu'entendíen que'l movimientu o la detención d'un cuerpu debíase puramente a si exercíase sobre ellos una fuercia, pero nunca entendiendo como tal al resfregón.
Arriendes d'ello, un cuerpu que se mueve con movimientu rectilliniu uniforme implica que nun esiste nenguna fuercia esterno neta o, dichu d'otra forma, un oxetu en movimientu nun se detién de forma natural si nun s'aplica una fuercia sobre él. Nel casu de los cuerpos en reposu, entiéndese que la so velocidá ye cero, polo que si esta camuda ye porque sobre esi cuerpu exercióse una fuercia neto.
Newton retomó la llei de la inercia de Galileo: l'enclín d'un oxetu en movimientu a siguir moviéndose nuna llinia recta, nun siendo que sufra la influencia de daqué que lu esvie del so camín. Newton supunxo que si la Lluna nun salía disparada en llinia recta, según una llinia tanxencial a la so órbita, deber a la presencia d'otra fuercia que lo emburriaba en direición a la Tierra, y qu'esviaba constantemente'l so camín convirtiéndolo nun círculu. Newton llamó a esta fuercia gravedá y creyó qu'actuaba a distancia. Nun hai nada que conecte físicamente la Tierra y la Lluna y sicasí la Tierra ta constantemente tirando de la Lluna escontra nós. Newton sirvir de la tercer llei de Kepler y dedució matemáticamente la naturaleza de la fuercia de la gravedá. Demostró que la mesma fuercia que faía cayer una mazana sobre la Tierra caltenía a la Lluna na so órbita.
La primer llei de Newton establez la equivalencia ente l'estáu de reposu y de movimientu rectilliniu uniforme. Supongamos un sistema de referencia S y otru S´ que se mueve respectu del primeru a una velocidá constante. Si sobre una partícula en reposu nel sistema S´ nun actúa una fuercia neto, el so estáu de movimientu nun va camudar y va permanecer en reposu respeuto del sistema S´ y con movimientu rectilliniu uniforme respectu del sistema S. La primer llei de Newton satisfacer en dambos sistemes de referencia. A estos sistemes nos que se satisfaen les lleis de Newton dáse-yos el nome de sistemes de referencia inerciales. Nengún sistema de referencia inercial tien preferencia sobre otru sistema inercial, son equivalentes: esti conceutu constitúi'l principiu de relatividá de Galileo o newtoniano.
L'enunciáu fundamental que podemos estrayer de la llei de Newton ye que
Esta espresión ye una ecuación vectorial, una y bones les fuercies lleven direición y sentíu. Per otra parte, cabo destacar que la variación cola que varia la velocidá correspuende a l'aceleración.
Sistemes de referencia inerciales[editar | editar la fonte]
La primer llei de Newton sirve pa definir un tipu especial de sistemes de referencia conocíos como sistemes de referencia inerciales, que son aquellos dende los que se repara qu'un cuerpu sobre'l que nun actúa nenguna fuercia neto mover con velocidá constante.
Un sistema de referencia con aceleración (y l'aceleración normal d'un sistema rotatoriu incluyir nesta definición) nun ye un sistema inercial, y l'observación d'una partícula en reposu n'el mesmu sistema nun va satisfaer les lleis de Newton (yá que se va reparar aceleración ensin la presencia de fuercia neto dalguna). Denominar sistemes de referencia non inerciales.

Por casu considérese una plataforma xirando con velocidá constante, ω, na qu'un oxetu ta atáu a la exa de xiru por aciu una cuerda, y supongamos dos observadores, unu inercial esternu a la plataforma y otru non inercial asitiáu sobre ella.[3]
- Observador inercial: dende'l so puntu de vista'l bloque mover en círculu con velocidá v y ta aceleráu escontra'l centru de la plataforma con una aceleración centrípeta . Esta aceleración ye consecuencia de la fuercia exercida pola tensión de la cuerda.
- Observador non inercial: pal observador que xira cola plataforma l'oxetu ta en reposu, a = 0. Esto ye, repara una fuercia ficticio que compensa la tensión por que nun haya aceleración centrípeta. Esa fuercia tien de ser . Esti observador siente la fuercia como si fuera perfectamente real, anque solo sía la consecuencia de l'aceleración del sistema de referencia en que s'atopa.
En realidá, ye imposible atopar un sistema de referencia inercial, yá que siempres hai dalgún tipu de fuercies actuando sobre los cuerpos; sicasí, siempres ye posible atopar un sistema de referencia nel que'l problema que teamos estudiando pueda tratase como si tuviéramos nun sistema inercial. En munchos casos, la Tierra ye un bonu aproximamientu de sistema inercial, yá que a pesar de cuntar con una aceleración traslacional y otra rotacional, dambes son del orde de 0.01 m/s² y, arriendes d'ello, podemos considerar qu'un sistema de referencia d'un observador na superficie terrestre ye un sistema de referencia inercial.
Aplicación de la primer llei de Newton[editar | editar la fonte]
Puede considerase como exemplu ilustrativu d'esta primer llei una bola atada a una cuerda, de cuenta que la bola xira siguiendo una trayeutoria circular. Por cuenta de la fuercia centrípeta de la cuerda (tensión), la masa sigue la trayeutoria circular, pero si en dalgún momentu la cuerda rompiérase, la bola tomaría una trayeutoria rectillinia na direición de la velocidá que tenía la bola nel intre de frayatu.

Tres el frayatu, la fuercia neto exercida sobre la bola ye 0, polo que va esperimentar, como resultáu d'un estáu de reposu, un movimientu rectilliniu uniforme.
Segunda llei de Newton o llei fundamental de la dinámica[editar | editar la fonte]
La segunda llei de Newton espresa que:
Mutationem motus proportionalem esse vi motrici impressæ, & fieri secundum lineam rectam qua vis illa imprimitur.[11]El cambéu de movimientu ye direutamente proporcional a la fuercia motriz impresa y asocede según la llinia recta a lo llargo de la cual aquella fuercia imprímese.[13]
Esta llei encargar de cuantificar el conceutu de fuercia. L'aceleración qu'adquier un cuerpu ye proporcional a encomalo neta aplicada sobre'l mesmu. La constante de proporcionalidad ye la masa del cuerpu (que puede ser o nun ser constante). Entender la fuercia como la causa del cambéu de movimientu y la proporcionalidad ente la fuercia impreso y el cambéu de la velocidá d'un cuerpu ye la esencia d'esta segunda llei.[14]
Si la masa ye constante[editar | editar la fonte]
Si la masa del cuerpu ye constante puede establecese la siguiente rellación, que constitúi la ecuación fundamental de la dinámica:
Onde m ye la masa del cuerpu la cual tien de ser constante pa ser espresada de tal forma. La fuercia neto qu'actúa sobre un cuerpu, tamién llamada fuercia resultante, ye'l vector suma de toles fuercies que sobre él actúen. Asina pos:[15]
- L'aceleración qu'adquier un cuerpu ye proporcional a encomalo aplicada, y la constante de proporcionalidad ye la masa del cuerpu.
- Si actúen delles fuercies, esta ecuación refierse a encomalo resultante, suma vectorial de toes elles.
- Esta ye una ecuación vectorial, depués débese cumplir componente a componente.
- N'ocasiones va ser útil recordar el conceutu de componentes intrínseques: si la trayeutoria nun ye rectillinia ye porque hai una aceleración normal, depués va haber tamién una fuercia normal (en direición perpendicular a la trayeutoria); si'l módulu de la velocidá varia ye porque hai una aceleración na direición de la velocidá (na mesma direición de la trayeutoria).
- La fuercia y l'aceleración son vectores paralelos, pero esto nun significa que'l vector velocidá sía paralelu a encomalo. Esto ye, la trayeutoria nun tien por qué ser tanxente a encomalo aplicada (namái asocede si siquier, la direición de la velocidá ye constante).
- Esta ecuación tien de cumplise pa tolos cuerpos. Cuando analicemos un problema con dellos cuerpos y distintes fuercies aplicaes sobre ellos, vamos deber entós tener en cuenta les fuercies qu'actúen sobre cada unu d'ellos y el principiu de superposición de fuercies. Vamos Aplicar la segunda llei de Newton pa cada unu d'ellos, teniendo en cuenta les interaiciones mutues y llogrando la fuercia resultante sobre cada unu d'ellos.

El principiu de superposición establez que si delles fuercies actúen igual o simultáneamente sobre un cuerpu, la fuercia resultante ye igual a la suma vectorial de les fuercies qu'actúen independientemente sobre'l cuerpu (regla del paralelogramu). Esti principiu apaez incluyíu nos Principia de Newton como Corolariu 1, dempués de la tercer llei, pero ye requisitu indispensable pa la comprensión y aplicación de les lleis, según pa la carauterización vectorial de les fuercies.[14] La fuercia va modificar l'estáu de movimientu, camudando la velocidá en módulu o direición. Les fuercies son causes que producen aceleraciones nos cuerpos. Polo tanto esiste una rellación causa-efeutu ente la fuercia aplicao y l'aceleración qu'esti cuerpu esperimenta.
D'esta ecuación llógrase la unidá de midida de la fuercia nel Sistema Internacional d'Unidaes, el Newton:
Per otra parte, si la fuercia resultante qu'actúa sobre una partícula nun ye cero, esta partícula va tener una aceleración proporcional a la magnitú de la resultante y en direición d'esta (por cuenta de que la masa siempres ye un esguilar positivu). La espresión anterior asina establecida ye válida tantu pa la mecánica clásica como pa la Teoría_de_la relatividá mecánica relativista.
Si la masa nun ye constante[editar | editar la fonte]
Si la masa de los cuerpos varia, como por casu un cohete que va quemando combustible, nun ye válida la rellación y hai que faer xenérica la llei por qu'incluya el casu de sistemes nos que pueda variar la masa. Pa ello primero hai que definir una magnitú física nueva, la cantidá de movimientu, que se representa pola lletra p y que se define como'l productu de la masa d'un cuerpu pola so velocidá, esto ye:
Newton enunció la so llei d'una forma más xeneral:
D'esta forma puede rellacionase la fuercia cola aceleración y cola masa, ensin importar qu'esta sía o nun sía constante. Cuando la masa ye constante sale de la derivada colo que queda la espresión:
Y llógrase la espresión clásica de la Segunda Llei de Newton:
La fuercia, poro, ye un conceutu matemáticu'l cual, por definición, ye igual a la derivada con respectu al tiempu del momentu d'una partícula dada, que'l so valor de la mesma depende de la so interaición con otres partícules. Poro, puede considerase la fuercia como la espresión d'una interaición. Otra consecuencia d'espresar la Segunda Llei de Newton usando la cantidá de movimientu ye lo que se conoz como principiu de caltenimientu de la cantidá de movimientu: si la fuercia total qu'actúa sobre un cuerpu ye cero, la Segunda llei de Newton diznos que
Esto ye, la derivada de la cantidá de movimientu con respectu al tiempu ye cero nos sos trés componentes. Esto significa que la cantidá de movimientu tien de ser constante nel tiempu en módulo direición y sentíu (la derivada d'un vector constante ye cero).[16]
La segunda llei de Newton solo ye válida en sistemes de referencia inerciales pero inclusive si'l sistema de referencia ye non inercial, puede utilizase la mesma ecuación incluyendo les fuercies ficticies (o fuercies inerciales). Unidaes y dimensiones de la fuercia:
- Unidaes S.I.:
- Sistema cegesimal: dina
- Equivalencia: 1 N= dinas
Cantidá de movimientu o momentu llinial[editar | editar la fonte]
Nel llinguaxe modernu la cantidá de movimientu o momentu llinial d'un oxetu definir por aciu la espresión . Esto ye, ye una magnitú vectorial proporcional a la masa y a la velocidá del oxetu. Partiendo d'esta definición y aplicando la llei fundamental de la mecánica de Newton, les variaciones de la cantidá de movimientu espresar en función de la fuercia resultante y l'intervalu de tiempu mientres el cual exerzse esta:
Tomando l'intervalu de tiempu de t1 a t2 ya integrando llógrase
Al vector I denominar impulsu llinial y representa una magnitú física que se manifiesta especialmente nes aiciones rápides o impautos, tales como choques, llevando módulo direición y sentíu. Nesti tipu d'aiciones convien considerar la duración del impautu y la fuercia exercida mientres el mesmu.
De la espresión llograda deduzse que l'impulsu llinial ye igual a la variación de la cantidá de movimientu. Si la fuercia resultante ye cero (esto ye, si nun s'actúa sobre l'oxetu) l'impulsu tamién ye cero y la cantidá de movimientu permanez constante. Llamamos a esta afirmación llei de caltenimientu del impulsu llinial, aplicada a un oxetu o una partícula.[17]
Les sos unidaes nel Sistema Internacional son
- Choque elásticu: permanecen constantes la cantidá de movimientu y la enerxía cinética. Dos partícules de mases distintes que solo interactúan ente sigo y que se mueven con velocidaes constantes y distintes una escontra la otra. Tres el choque, permanez constante la cantidá de movimientu y la enerxía cinética.
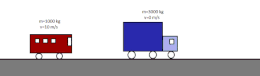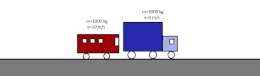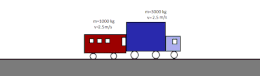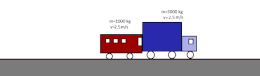
- Choque inelástico: permanez constante la cantidá de movimientu y varia la enerxía cinética. De resultes, los cuerpos que topeten pueden sufrir deformaciones y aumentu de la so temperatura. Tres un choque totalmente inelástico, dambos cuerpos tienen la mesma velocidá. La suma de les sos enerxíes cinétiques ye menor que la inicial porque una parte d'esta haise tresformáu en enerxía interna; na mayoría de los casos apuerta a estenada en forma de calor debío al calentamientu producíu nel choque. Nel casu ideal d'un choque perfectamente inelástico ente oxetos macroscópicos, estos permanecen xuníos ente sigo tres el choque.[18]
Aplicaciones de la segunda llei de Newton[editar | editar la fonte]
Ente les posibles aplicaciones de la Segunda Llei de Newton, pueden destacar:

- Cayida llibre: ye un movimientu que se repara cuando un oxetu déxase cayer dende una ciertu altor sobre la superficie de la tierra. Pa estudiar el movimientu escueye un sistema de coordenaes onde l'orixe de la exa y ta sobre esta postrera. Nesti sistema tantu la velocidá de cayida como l'aceleración de la gravedá tienen signu negativu. Nel exemplu representáu, supónse que l'oxetu déxase cayer dende'l reposu, pero ye posible que caya dende una velocidá inicial distinta de cero.[18]

- Pendilexu simple: partícula de masa m suspendida del puntu O por un filo inextensible de llargor l y de masa despreciable. Si la partícula mover a una posición θ0 (ángulu que fai'l filo cola vertical) y depués suéltase, el pendilexu empieza a bazcuyar. El pendilexu describe una trayeutoria circular, un arcu d'una circunferencia de radiu l. Les fuercies qu'actúen sobre la partícula de masa m son dos, el pesu y la tensión T del filo.
Si aplícase la segunda llei, na direición radial:
onde an representa l'aceleración normal a la trayeutoria. Conocíu'l valor de la velocidá v na posición angular puede determinase la tensión T del filo. Esta ye máxima cuando'l pendilexu pasa pola posición d'equilibrio
,
onde'l segundu términu representa la fuercia centrífuga.
Y la tensión ye mínima, nos estremos de la so trayeutoria, cuando la velocidá ye cero
na direición tanxencial:
onde at representa l'aceleración tanxente a la trayeutoria.
Tercer llei de Newton o principiu d'aición y reaición[editar | editar la fonte]
La tercer llei de Newton establez que siempres qu'un oxetu exerz una fuercia sobre un segundu oxetu, este exerz una fuercia d'igual magnitú y direición pero en sentíu opuestu sobre'l primeru. Con frecuencia enúnciase asina: A cada aición siempres s'opón una reaición igual pero de sentíu contrariu. En cualquier interaición hai un par de fuercies d'aición y reaición asitiaes na mesma direición con igual magnitú y sentíos opuestos. La formulación orixinal de Newton ye:
Actioni contrariam semper & æqualem esse reactionem: sive corporum duorum actiones in se mutuu semper esse æquales & in partes contraries dirigi.[11]Con toa aición asocede siempres una reaición igual y contraria: quier dicir que les aiciones mutues de dos cuerpos siempres son iguales y empobinaes en sentíu opuestu.[13]
Esta tercer llei de Newton ye dafechu orixinal (pos los dos primeres yá fueren propuestes d'otra manera por Galileo, Hooke y Huygens) y fai de les lleis de la mecánica un conxuntu lóxico y completo.[19] Espón que per cada fuercia qu'actúa sobre un cuerpu, este realiza una fuercia d'igual intensidá, pero de sentíu contrariu sobre'l cuerpu que lu produció. Dichu d'otra forma, les fuercies, asitiaes sobre la mesma recta, siempres se presenten en pares d'igual magnitú y de direición, pero con sentíu opuestu. Si dos oxetos interaccionan, la fuercia F12, exercida pol oxetu 1 sobre l'oxetu 2, ye igual en magnitú con mesma direición pero sentíos opuestos a encomalo F21 exercida pol oxetu 2 sobre l'oxetu 1:[20]
Esti principiu presupon que la interaición ente dos partícules arrobínase instantáneamente nel espaciu (lo cual riquiría velocidá infinita), y na so formulación orixinal nun ye válidu pa fuercies electromagnétiques yá que estes nun s'arrobinen pel espaciu de manera instantánea sinón que lo faen a velocidá finita "c". Esti principiu rellaciona dos fuercies que nun tán aplicaes al mesmu cuerpu, produciendo nellos aceleraciones distintes, según sían les sos mases. Otra manera, caúna d'eses fuercies obedez por separáu a la segunda llei. Xunto coles anteriores lleis, esta dexa enunciar los principios de caltenimientu del momentu llinial y del momentu angular.[14]
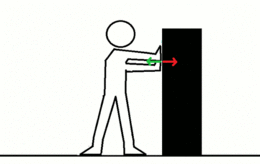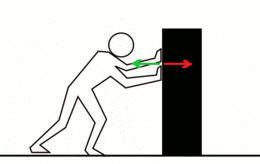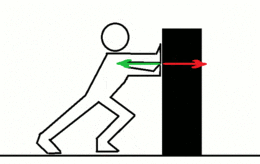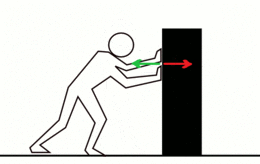
Aplicaciones de la Tercer Llei de Newton[editar | editar la fonte]
Dellos exemplos onde actúen forzar aición-reaición son los siguientes:[20]
- Si una persona emburria a otra de pesu similar, los dos mover cola mesma velocidá pero en sentíu contrariu.
- Cuando saltamos, emburriamos a la tierra escontra baxo, que nun se mueve por cuenta de la so gran masa, y esta embúrrianos cola mesma intensidá escontra riba.
- Una persona que rema nun bote emburria l'agua col remu nun sentíu y l'agua respuende emburriando'l bote en sentíu opuestu.
- Cuando caminamos emburriamos a la tierra escontra tras colos nuesos pies, a lo que la tierra respuende emburriándonos a nós palantre, faciendo qu'avancemos.
- Cuando se dispara una bala, la esplosión de la pólvora exerz una fuercia sobre la pistola (que ye'l retrocesu que sufren les armes de fueu al ser disparaes), que reacciona exerciendo una fuercia d'igual intensidá pero en sentíu contrariu sobre la bala.
- La fuercia de reaición qu'una superficie exerz sobre un oxetu sofitáu nella, llamada fuercia normal con direición perpendicular a la superficie.
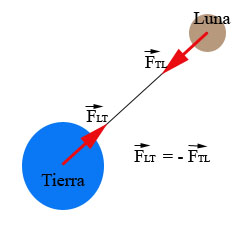
- Les fuercies a distancia nun son una esceición, como la fuercia que la Tierra exerz sobre la Lluna y viceversa, la so correspondiente pareya d'aición y reaición:[21]
La fuercia qu'exerz la Tierra sobre la Lluna ye esautamente igual (y de signu contrariu) a la qu'exerz la Lluna sobre la Tierra y el so valor vien determináu pola llei de gravitación universal enunciada por Newton, qu'establez que la fuercia qu'exerz un oxetu sobre otru ye direutamente proporcional al productu de les sos mases, ya inversamente proporcional al cuadráu de la distancia que los dixebra. La fuercia que la Tierra exerz sobre la Lluna ye la responsable de qu'esta non se sala de la so órbita circular.
Amás, la fuercia que la Lluna exerz sobre la Tierra ye tamién responsable de les marees, pos conforme la Lluna xira alredor de la Tierra esta exerz una fuercia d'atraición sobre la superficie terrestre, que alza los mares y océanos, alzando dellos metros el nivel de l'agua en dellos llugares; por esti motivu esta fuercia tamién se llama fuercia de marea. La fuercia de marea de la lluna componer cola fuercia de marea del sol apurriendo'l fenómenu completu de les marees.
Llimitaciones y xeneralizaciones posteriores[editar | editar la fonte]
Dempués de que Newton formulara los trés famoses lleis, numberosos físicos y matemáticos fixeron contribuciones pa da-yos una forma más xeneral o de más bona aplicación a sistemes non inerciales o a sistemes con lligadures. Una d'estes primeres xeneralizaciones foi'l principiu de d'Alembert de 1743 que yera una forma válida pa cuando esistieren lligadures que dexaba resolver les ecuaciones ensin necesidá de calcular explícitamente el valor de les reaiciones acomuñaes a diches lligadures.[22]
Pola mesma dómina, Lagrange atopó una forma de les ecuaciones de movimientu válida pa cualquier sistema de referencia inercial o non-inercial ensin necesidá d'introducir fuercies ficticies.[23] Yá que ye un fechu conocíu que les Lleis de Newton, tal como fueron escrites, namái son válides a los sistemes de referencia inerciales, o más precisamente, p'aplicales a sistemes non-inerciales, riquen la introducción de les llamaes fuercies ficticies, que se porten como fuercies pero nun tán provocaes direutamente por nenguna partícula material o axente concretu, sinón que son un efeutu aparente del sistema de referencia non inercial.[24]
Más tarde la introducción de la teoría de la relatividá obligó a modificar la forma de la segunda llei de Newton (ver ()), y la mecánica cuántica dexó claro que les lleis de Newton o la relatividá xeneral namái son aproximamientos al comportamientu dinámicu n'escales macroscópicas. Tamién se conxeturaron dellos cambeos macroscópicas y non-relativistes, basaes n'otros supuestos como la dinámica MOND.
Xeneralizaciones relativistes[editar | editar la fonte]
Les lleis de Newton constitúin tres principios aproximao válidos pa velocidaes pequeñes. La forma en que Newton formular nun yera la más xeneral posible. De fechu la segunda y tercer lleis na so forma orixinal nun son válides en teoría de la relatividá mecánica relativista sicasí formulaos de forma llixeramente distinta la segunda llei ye válida, y la tercer llei almite una formulación menos restrictiva que ye válida en mecánica relativista.
- Primer llei, n'ausencia de campos gravitatorios nun riquir cambeos. Nun espaciu-tiempu planu una llinia recta cumple la condición de ser xeodésica. En presencia de curvatura nel espaciu-tiempu la primer llei de Newton sigue siendo correuta si sustituyimos la espresión llinia recta per llinia xeodésica.
- Segunda llei. Sigue siendo válida si dizse que la fuercia sobre una partícula coincide cola tasa de cambéu del so momentu llinial. Sicasí, agora la definición pel momento llinial na teoría newtoniana y na teoría relativista difieren. Na teoría newtoniana el momentu llinial definir según () ente que na teoría de la relatividá d'Einstein definir por aciu ():
(1a)
(1b)
- onde m ye la masa invariante de la partícula y la velocidá d'ésta midida dende un ciertu sistema inercial. Esta segunda formulación de fechu inclúi implícitamente definición () según la cual el momentu llinial ye'l productu de la masa pola velocidá. Como esi supuestu implícitu nun se cumple nel marcu de la teoría de la relatividá d'Einstein (onde la definición ye ()), la espresión de la fuercia en términos de l'aceleración na teoría de la relatividá toma una forma distinta. Por casu, pal movimientu rectilliniu d'una partícula nun sistema inercial tiense que la espresión equivalente a (2a) ye:
(2b)
- Si la velocidá y la fuercia nun son paraleles, la espresión sería la siguiente:
(2c)
- Nótese qu'esta última ecuación implica que salvu pal movimientu rectilliniu y el circular uniforme, el vector d'aceleración y el vector de fuercia nun van ser parelelos y van formar un pequeñu ángulu rellacionáu col ángulu que formen l'aceleración y la velocidá.
- Tercer Llei de Newton. La formulación orixinal de la tercer llei per parte de Newton implica que l'aición y reaición, amás de ser de la mesma magnitú y opuestes, son colineales. Nesta forma la tercer llei non siempres se cumple en presencia de campos magnéticos. En particular, la parte magnética de la fuercia de Lorentz que s'exercen dos partícules en movimientu nun son iguales y de signu contrariu. Esto puede trate por cómputu direutu. Daes dos partícules puntuales con cargues q1 y q2 y velocidaes , la fuercia de la partícula 1 sobre la partícula 2 ye:
onde d la distancia ente los dos partícules y ye'l vector direutor unitariu que va de la partícula 1 a la 2. Análogamente, la fuercia de la partícula 2 sobre la partícula 1 ye:
Emplegando la identidá vectorial , puede trate que la primer fuercia ta nel planu formáu por y que la segunda fuercia ta nel planu formáu por y . Poro, estes fuercies non siempres resulten tar sobre la mesma llinia, nin polo xeneral son d'igual magnitú
Teorema de Ehrenfest[editar | editar la fonte]
El teorema de Ehrenfest dexa xeneralizar les lleis de Newton al marcu de la mecánica cuántica. Magar en dicha teoría nun ye lícitu falar de fuercies o de trayeutoria, puede falase de magnitúes como momentu llinial y potencial de manera similar a como se fai en mecánica newtoniana.
En concretu la versión cuántica de la segunda Llei de Newton afirma que la derivada temporal del valor esperáu del momentu d'una partícula nun campu iguala al valor esperáu de la "fuercia" o valor esperáu del gradiente del potencial:
Onde:
- ye'l potencial del que derivar les fuercies».
- , son les funciones d'onda de la partícula y la so complexa conxugada.
- denota el operador nabla.
Ver tamién[editar | editar la fonte]
- Sistema inercial
- Mecánica clásica
- Física clásica
- Momentu d'inercia
- Cantidá de movimientu
- Inercia
- Fuercia
- Choque elásticu
Notes[editar | editar la fonte]
- ↑ Esiste, amás, una versión previa nun fragmentu manuscritu de 1684 que lleva como títulu De motu corporum in mediis regulariter cedentibus. Per otru llau, nesi mesmu testu queda claro que, orixinalmente, Newton había propuestu cinco lleis, de les cualos la cuarta yera l'principiu de relatividá de Galileo.
- ↑ Los primeros esfuercios rexistraos pol ser humanu p'axuntar sistemáticamente la conocencia sobre'l movimientu de los cuerpos vienen de l'antigua Grecia. Na filosofía natural establecida por Aristóteles les esplicaciones de los fenómenos físicos deducir de la hipótesis sobre'l mundu y non de la esperimentación.
- ↑ Sotu destaca ensin dulda como un magníficu profesor, el meyor simplificador na clasificación de los movimientos, y quien más comenenciudu taba n'unificar les formulaciones astractes col mundu físicu real.
- ↑ Domingo de Soto formulara más de cincuenta años tras que'l movimientu de cayida yera un movimientu uniformemente aceleráu, unijórmiter disformis con respectu al tiempu. Y esi yera'l principiu que Galileo precisaba.
- ↑ Una meyora bien importante deber a Galileo (1564-1642) quien introdució'l métodu científicu, qu'enseña que non siempres se debe creer nes conclusiones intuitives basaes na observación inmediata, pos esto lleva de cutiu a equivocaciones. Galileo realizó un gran númberu d'esperiencies nes que se diben camudando llixeramente les condiciones del problema y midió los resultaos en cada casu. D'esta manera pudo extrapolar les sos observaciones hasta llegar a entender un esperimentu ideal.
- ↑ Foi Isaac Newton (hacia 1690) el primeru en dar una formulación completa de les lleis de la mecánica ya inventó los procedimientos matemáticos necesarios pa esplicalos y llograr información a partir d'ellos.
Referencies[editar | editar la fonte]
- ↑ Pickover, 2009, páxs. 132-170.
- ↑ Williams, Dudley y John Spangler, Physics for Science and Engineering, ápud Pickover (2009, pp. 133)
- ↑ 3,0 3,1 3,2 3,3 Medina Domínguez, Alejandro; Ovejero Sánchez, Jesús. «Ley de Newton y les sos aplicaciones». Física I. Cursu 2010/11. http://ocw.usal.es/ensenanzas-tecnicas/fisica-i/contenidos/temes_por_separáu/2_ap_newton1011.pdf.
- ↑ Tipler y Mosca, 2006, páxs. 4.
- ↑ Navarro, Víctor. «Juan de Celaya». mcnbiografias.com. Consultáu'l 16 de mayu de 2015.
- ↑ Battaner, Eduardo (2011). Física de les Nueches Estrellaes. Tusquets. ISBN 9788483833421. «Tolos países tienen l'enclín a atribuyir a dalgunos de los sos pretéritos fíos los grandes descubrimientos. Nós paez que non. Menéndez Pelayo cúntanos que Juan de Celaya yera escolásticu dexeneráu, recalcitrante y bárbaru. ¡Inxustos epítetos pal científicu qu'enunció per primer vegada una de les lleis más importantes de la Física!»
- ↑ Navarro, Víctor. «Domingo de Soto». mcnbiografias.com. Consultáu'l 16 de mayu de 2015.
- ↑ 8,0 8,1 8,2 Pérez Camacho, Juan José; Sols Lucia, Ignacio (1994). «Domingo de Soto nel orixe de la ciencia moderna». Revista de filosofía (12): páxs. 455-476. ISSN 0034-8244. http://revistas.ucm.es/index.php/RESF/article/download/RESF9494220455A/11294. Consultáu'l 16 de mayu de 2015.
- ↑ de Sotu, Domingo. «7», Quaestiones.
- ↑ Dugas, Rene (2008). «La escuela inglesa dende Descartes hasta Newton». Newton. Vida, pensamientu y obra: páxs. 116-131.
- ↑ 11,0 11,1 11,2 Newton Leges (The Latin Library)
- ↑ Rada García, Eloy (trad.) (2003). apud. Newton. Vida, pensamientu y obra, páx. 199. «Principio matemáticos de la filosofía natural». A costazos de xigantes. Les grandes obres de la física y l'Astronomía (Barcelona: Crítica).
- ↑ 13,0 13,1 Isaac Newton, estractos de Principios matemáticos de la filosofía natural, cit., páx. 199.
- ↑ 14,0 14,1 14,2 M. Sebastiá, José Sebastiá (2013). «Les Lleis de Newton de la mecánica». Didáctica de les ciencies esperimental y social (27): p. 210. ISSN 02144379. https://ojs.uv.es/index.php/dces/article/viewFile/2241/3323. Consultáu'l 9 de xunetu de 2015.
- ↑ Departamentu de Física Aplicada III. Universidá de Sevilla (ed.): «sistema_de_part%C3%ADculas Propiedaes d'un sistema de partícules». Laplace.
- ↑ Tipler y Mosca, 2006, páxs. 230.
- ↑ Tipler y Mosca, 2006, páxs. 207.
- ↑ 18,0 18,1 Tipler y Mosca, 2006, páxs. 217.
- ↑ Pickover, 2009, p. 137.
- ↑ 20,0 20,1 Tipler y Mosca, 2006, páxs. 98.
- ↑ Tipler y Mosca, 2006, páxs. 87.
- ↑ A. Fernández Rañanada: Dinámica clásica, pp. 131-33.
- ↑ A. Fernández Rañanada: Dinámica clásica, pp. 102-09.
- ↑ A. Fernández Rañanada: Dinámica clásica, pp. 366-75.
Bibliografía[editar | editar la fonte]
- Alonso, Marcelo; Finn, Edward J. (1998). Física 1. ISBN 9789684442238.
- Bell, Eric T. (1986). On the Seashore: Newton (n'inglés). ISBN 978-0671628185.
- Christianson, Gale Y. (1985). In the Presence of the Creator: Isaac Newton and His Times (n'inglés). ISBN 978-0029051900.
- Da Costa Andrade, Edward N. (1979). Sir Isaac Newton (n'inglés). ISBN 978-0313220227.
- De Gandt, François (2014). Force and Geometry in Newton's "Principia" (Princeton Legacy Library) (n'inglés). ISBN 978-0691033679.
- De Juana, José María (2003). Física Xeneral 1. Pearson Prentice Hall. ISBN 84-205-3342-4.
- Fauvel, John; Flood, Raymond; Shortland, Michael; Wilson, Robin (1988). Let Newton Be! (n'inglés). ISBN 978-0198539247.
- Ortega Girón, Manuel R. (1989-2010). leición de Física (4 volumes). Monytex. ISBN 84-404-4290-4.
- Pickover, Clifford A. (2009). De Arquímedes a Hawking. Les lleis de la ciencia y el so descubridores editorial = Críticu. ISBN 978-84-9892-003-1.
- Sagan, Carl (1981). Cosmos. ISBN 2-86374-075-X.
- Sears, W.; Zemansky, M.W.; Young, H.D.; Freedman, F. (1999). Física Universitaria 1. Addison-Wesley-Longman. ISBN 968-444-277-7.
- Tipler, Paul Allen; Mosca, Gene (2006). Física pa la ciencia y la teunoloxía 2. Reverté. ISBN 8429144129.
- Tippens, Paul Y. (2007). Física Conceutu y aplicaciones. Méxicu: McGraw-Hill. ISBN 9789701062609.
- Westfall, Richard S. (1983). Never at Rest: A Biography of Isaac Newton (Cambridge Paperback Library) (n'inglés). ISBN 978-0521274357.
- Zitzewitz, Paul W.; Neff, Robert F. (1995). Física 1. McGraw-Hill. ISBN 978-958-600-381-0.
Enllaces esternos[editar | editar la fonte]
- Wikipedia:Artículos con plantíes de notes d'encabezamientu enllaciando a páxines que nun esisten
- Wikipedia:Revisar traducción
- Principios y lleis físiques
- Mecánica newtoniana
- Ciencia y teunoloxía del Reinu Xuníu
- Wikipedia:Collaboración UPM y Wikimedia España
- Isaac Newton
- Wikipedia:Páxines que usen un formatu anticuáu d'etiquetes matemátiques










































