Teorema de Tales
Hai dos teoremes que reciben el nome de teorema de Tales.
Primer teorema[editar | editar la fonte]
Seyan dos reutes (d) y (d') n'aldu y concurrentes nún puntu O. Seyan A y A' dos puntos de (d), y B y B' dos puntos de (d'). Entós:
Ye dicir, que la igualdá de los cocientes equival al paralelismu. Esti teorema afita asina una rellación ente l'álxebra y la xeometría.
La primera figura correspuende a midíes alxebraiques positives - los vectores OA, OA', OB y OB' tienen el mesmu aldu que les reutes (d) y (d'), y la segunda a cocientes negativos.
Si s'aplica el teorema, tenemos arriendes otra consecuencia: si s'orienta de la mesma manera les dos reutes paraleles (AB) y (A'B'), ye dicir col mesmu vector, entós el tercer cociente (de midides alxebraiques): A'B' / AB ye igual a los dos anteriores.
A vegaes resérvase el nome de teorema de Tales al sen direutu de l'equivalencia, y l'otru sen recibe'l nome de recíproca del teorema de Tales.
Esti teorema ye un casu particular de los Triángulos semeyos o asemeyaos.
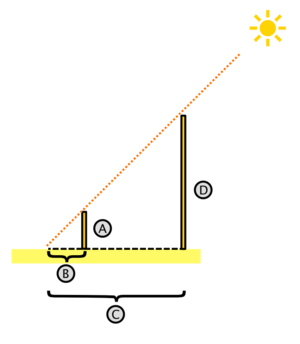
Una aplicación interesante ye pa midir l'altura de daqué.(Exemplu: árbol)
- Midimos la llonxitú de la so solombra a una hora determinada. = C
- Midimos la llonxitú de la solombra d'un oxetu pequeñu (por exemplu un llápiz) nel mesmu intre. = B
- Midimos la llonxitú real del mesmu cuerpu. = A
Y obtenemos au D ye l'altura real del árbol.
Tamién se pue rellacionar pa midir una distancia, cuya finidad no pueda ser midida, y apoyándose en un punto, se puede lograr.
Segundu teorema[editar | editar la fonte]
Seya C un puntu de la circunferencia de diámetru [AB], distintu d'A y de B. Entós l'ángulu ACB ye reutu.

Este teorema ya un casu particular de una propiedá de los puntos cocíclicos.
Prueba: OA = OB = OC = r, radiu del círculu. Poro, OAC y OBC son isósceles. La suma de los ángulos del triángulu ABC val
(radianes).
Dividiendo por dos, obtiense
(o 90º).
Arriendes, dizse que la bisectriz d'un triángulu corta al llau aviesu del ángulu cola bisectriz en dos segmentos proporcionales





