Ecuación en derivaes parciales

Ecuación en derivaes parciales
	ecuación diferencial

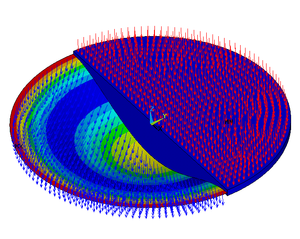
Flexón elástica d'una placa circular empotrada na so contorna so l'acción d'una carga vertical distribuyida uniformemente, que ye solución de la ecuación de Lagrange de plaques; la solución amosada foi llograda numbéricamente por aciu Ansys.

Variación del perfil de temperatures solución de la ecuación del calor nun problema bidimensional.

En matemátiques una ecuación en derivaes parciales (dacuando embrivíu como EDP) ye aquella ecuación diferencial que les sos incógnites son funciones de diverses variables independientes, cola peculiaridá de qu'en dicha ecuación figuren non solo les mesmes funciones sinón tamién les sos derivaes. Tienen qu'esistir funciones d'a lo menos dos variables independientes.^[1] O bien una ecuación qu'arreye una función matemática $o$ de delles variables independientes $x,y,z,t,...$ y les derivaes parciales de $o$ respectu d'eses variables. Les ecuaciones en derivaes parciales emplegar na formulación matemática de procesos de la física y otres ciencies que suelen tar distribuyíos nel espaciu y el tiempu. Problemes típicos son l'espardimientu del soníu o del calor, la electrostática, la electrodinámica, la dinámica de fluyíos, la elasticidá, la mecánica cuántica y munchos otros. Conocer tamién como ecuaciones diferenciales parciales. Participaron, al entamu, nel so estudiu los franceses d'Alembert, Fourier, matemáticos de la dómina napoleónica.

Introducción

Una ecuación diferencial en derivaes parciales (EDP) pa la función $o(x_{1},...x_{n})\,$ tien la siguiente forma:

$F(x_{1},\cdots x_{n},o,{\frac {\partial }{\partial x_{1}}}o,\cdots {\frac {\partial }{\partial x_{n}}}o,{\frac {\partial ^{2}}{\partial x_{1}\partial x_{1}}}o,{\frac {\partial ^{2}}{\partial x_{1}\partial x_{2}}}o,\cdots )=0\,$

onde $\scriptstyle F$ ye una función llinial de $o\,$ y los sos derivaes si:

$F(\lambda o+\mu w)=\lambda F(o)+\mu F(w),$

Si $F\,$ ye una función llinial de $o\,$ y les sos derivaes, entós la EDP ye llinial. Exemplos comunes de EDPs son la ecuación del calor, la ecuación d'onda y la ecuación de Laplace. Una ecuación diferencial en derivaes parciales simple pue ser:

{\frac {\partial o}{\partial x}}(x,y)=0\,

onde o ye una función de x y y. Esta rellación implica que los valores de o(x, y) son dafechu independientes de x. Polo tanto la solución xeneral d'esta ecuación diferencial ye:

$o(x,y)=f(y),\,$

onde f ye una función arbitraria de y. La ecuación diferencial ordinaria (Similar a la EDP, pero con funciones d'una variable) análoga ye

${\frac {du}{dx}}=0,\,$

que tien la siguiente solución

$o(x)=c,\,$

Onde c ye cualquier valor constante (independiente de x). Estos dos exemplos ilustren que les soluciones xenerales de les ecuaciones diferenciales ordinaries caltener con constantes, pero les soluciones de les ecuaciones diferenciales en derivaes parciales xeneren funciones arbitraries. Una solución d'una ecuación en derivaes parciales xeneralmente nun ye única; de tala forma que tiénense qu'apurrir condiciones adicionales de contorna capaces de definir la solución de forma única. Por casu, nel casu senciellu anterior, la función $\scriptstyle f(y)\,$ puede determinase si $\scriptstyle o\,$ especifícase sobre la llinia $\scriptstyle x=0\,$ .

Notación y exemplos

Nes ecuaciones diferenciales en derivaes parciales ye bien común denotar les derivaes parciales emplegando sub-índices (Notación tensorial). Esto ye:

$o'_{x}={\partial o \over \partial x},\qquad o''_{xy}={\partial ^{2}o \over \partial y\,\partial x}={\partial \over \partial y}\left({\partial o \over \partial x}\right)$

Especialmente na física matemática, suelse preferir el operador nabla (qu'en coordenaes cartesianes escríbese como $\nabla =(\partial _{x},\partial _{y},\partial _{z})$ pa les derivaes espaciales y un puntu ( ${\dot {o}}$ ) pa les derivaes qu'arreyen el tiempu, por casu pa escribir la Ecuación d'onda (vease más embaxo) como : ${\ddot {o}}=c^{2}\Delta o\,$ (notación matemática)

{\ddot {o}}=c^{2}\nabla ^{2}o\,

(notación física)

Solución xeneral y solución completa

Toa ecuación diferencial en derivaes parciales de primer orde tien una solución dependiente d'una función arbitraria, que se denomina usualmente solución xeneral de la EDP. En munches aplicaciones físiques esta solución xeneral ye menos importante que les llamaes soluciones completes, que frecuentemente pueden llograse pol métodu de separación de variables.

Una solución completa ye una solución particular de la EDP que contién tantes constantes arbitraries independientes como variables independientes intervienen na ecuación. Por casu la integración de les ecuaciones del movimientu d'un sistema mecánicu por aciu el métodu basáu na ecuación de Hamilton-Jacobi rique una integral completa, ente que la solución xeneral resulta menos interesante dende'l puntu de vista físicu.

Esistencia y unicidá

Anque l'asuntu de la esistencia y unicidá de les soluciones de les ecuaciones diferenciales ordinaries tien una respuesta bien satisfactoria resumida nel teorema de Picard-Lindelöf, el mesmu asuntu pa les ecuaciones en derivaes parciales ta lloñe de tar satisfactoriamente resueltu. Anque esiste un teorema xeneral, el teorema de Cauchy-Kovalevskaya, qu'afirma que pa una EDP, que ye analítica na función incógnita y les sos derivaes, tien una única solución analítica. Anque esta resultancia que paez establecer la esistencia y unicidá de la soluciones, apaecen exemplos de EDP de Ecuación diferencial#Orde de la ecuación primer orde que los sos coeficientes tienen derivaes de cualesquier orde (anque ensin ser analítiques) pero que nun tienen solución.^[2] Inclusive si la solución d'una EDP esiste y ye única, ésta puede tener propiedaes indeseables.

Un exemplu de comportamientu patolóxicu ye la secuencia de problemes de Cauchy dependientes del parámetru n pa la ecuación de Laplace:

${\frac {\partial ^{2}o}{\partial x^{2}}}+{\frac {\partial ^{2}o}{\partial y^{2}}}=0,\,$

con condiciones iniciales

$o(x,0)=0,\qquad {\frac {\partial o}{\partial y}}(x,0)={\frac {\sin nx}{n}},\,$

Onde n ye un enteru. La derivada de o con al respective de y averar a 0 uniformemente en x a midida que n amóntase, pero la solución ye:

$o(x,y)={\frac {(\sinh ny)(\sin nx)}{n^{2}}}.\,$

Esta solución averar a infinitu si nx nun ye un enteru múltiplu de π para cualquier valor de y. El problema de Cauchy pa la ecuación de Laplace denominar mal propuestu o mal definíu, yá que la solución nun depende de cutio de los datos del problema. Estos problemes mal definíos nun son usualmente satisfactorios pa les aplicaciones físiques.

Clasificación de les EDP de segundu orde

Les EDP de segundu orde clasifíquense davezu dientro de cinco tipos de EDP que son d'interés fundamental, de siguío danse exemplos d'estos cinco tipos:

Ecuación	Nome	-----
$\nabla ^{2}o=0$	Laplace	-----	$\nabla ^{2}o=f$	Poisson	-----
${\frac {\partial ^{2}o}{\partial t^{2}}}=c^{2}\nabla ^{2}o$	Hiperbólica \|-----	${\frac {\partial o}{\partial t}}=k\nabla ^{2}o$	Parabóliques
$\nabla ^{2}o=ku$	Helmholtz	Elíptica

Con mayor xeneralidá, si tiense una ecuación de segundu orde del tipu:

(*) $Au_{xx}+2Bu_{xy}+Cu_{yy}+Du_{x}+Eu_{y}+F=0\quad$

Con estos coeficientes monta la siguiente matriz:

$Z={\begin{bmatrix}A&B\\B&C\end{bmatrix}}$

En función del determinante la ecuación (*):

dizse que ye elíptica si la matriz Z tien un determinante mayor a 0.
dizse que ye parabólica si la matriz Z tien un determinante igual a 0.
dizse que ye hiperbólica si la matriz Z tien un determinante menor a 0.

Nomes d'oxetos de la xeometría analítica y llámense cóniques.

EDP d'orde cimeru

Magar les EDP de segundu orde aplicar a una inmensa cantidá de fenómenos físicos; otra cantidá menor de procesos físicos topen solución en EDP d'ordes cimeros, como exemplos podemos citar:

Flexón mecánica d'una placa elástica:

${\frac {\partial ^{4}w}{\partial x^{4}}}+2{\frac {\partial ^{4}w}{\partial x^{2}\partial y^{2}}}+{\frac {\partial ^{4}w}{\partial y^{4}}}={\frac {q(x,y)}{D}}$

Vibración flexonal d'una viga:

${\frac {\partial ^{2}}{\partial x^{2}}}\left[EI{\frac {\partial ^{2}y}{\partial x^{2}}}\right]+\rho A{\frac {\partial ^{2}y}{\partial t^{2}}}=p(x,t)$

Ecuación de Korteweg-de Vries, que tien soluciones de tipu solitón,

${\frac {\partial v}{\partial t}}+v{\frac {\partial v}{\partial x}}+\mu {\frac {\partial ^{3}v}{\partial x^{3}}}=0$

Ver tamién

Referencies

↑ Mijáilov: "Ecuaciones diferenciales en derivaes parciales", Editorial Mir, Moscú
↑ Lewy, 1957.

Bibliografía

Aranda Iriarte, José Ignacio (2011) Apuntes d'ecuaciones diferenciales II (EDPs).
Ireneo Peral, Primer cursu d'ecuaciones en derivaes parciales. Departamentu de Matemátiques, Universidá Autónoma de Madrid.
R. Courant and D. Hilbert, Methods of Mathematical Physics, vol II. Wiley-Interscience, New York, 1962.
Evans, Lawrence C. (2010). Partial Differential Equations, 2ª 19 (n'inglés), AMS. ISBN 978-0-8218-4974-3.
J. Jost, Partial Differential Equations, Springer-Verlag, New York, 2002.
Hans Lewy (1957) An example of a smooth linear partial differential equation without solution. Annals of Mathematics, 2nd Series, 66(1),155-158.
I.G. Petrovskii, Partial Differential Equations, W. B. Saunders Co., Philadelphia, 1967.
Y. Pinchover and J. Rubinstein, An Introduction to Partial Differential Equations, Cambridge University Press, Cambridge, 2005. ISBN 978-0-521-84886-2
A. D. Polyanin, Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC Press, Boca Raton, 2002. ISBN 1-58488-299-9
A. D. Polyanin and V. F. Zaitsev, Handbook of Nonlinear Partial Differential Equations, Chapman & Hall/CRC Press, Boca Raton, 2004. ISBN 1-58488-355-3
A. D. Polyanin, V. F. Zaitsev, and A. Moussiaux, Handbook of First Order Partial Differential Equations, Taylor & Francis, London, 2002. ISBN 0-415-27267-X
T. Roubíček: Nonlinear Partial Differential Equations with Applications. Birkhäuser, Basel, 2nd Ed.: 2013, SBN: 978-3-0348-0512-4 (DOI: 10.1007/978-3-0348-0513-1).
Iório, Valéria, EDP un cursu de graduación, Institutu de matemátiques y ciencia allegaes, UNI, Lima (1999)- lima.
Duff-Naylor, Differential equations and applied mathematics, John New York: Wiley and Sons, 1966.
D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.

Enllaces esternos

Wikillibros tien un llibru o manual sobre Partial Differential Equations. (n'inglés).
Partial Differential Equations: Exact Solutions at EqWorld: The World of Mathematical Equations.
Partial Differential Equations: Index at EqWorld: The World of Mathematical Equations.
Partial Differential Equations: Methods at EqWorld: The World of Mathematical Equations.
Example problems with solutions Archiváu 2017-07-01 en Wayback Machine at exampleproblems.com
Weisstein, Eric W. «Partial Differential Equations» (inglés). MathWorld. Wolfram Research.
Dispersive PDE Wiki
NEQwiki, the nonlinear equations encyclopedia

[1] Mijáilov: "Ecuaciones diferenciales en derivaes parciales", Editorial Mir, Moscú

[2] Lewy, 1957.

[1]

[2]