Toroide

En xeometría'l toroide ye la superficie de revolución xenerada por una curva plana zarrada simple que xira alredor d'una recta esterior coplanar (la exa de rotación) cola que non se interseca. La so forma correspondese cola superficie de los oxetos que, na fala cotidiana, denominense argolles, aniellos, aros, rosques, dones o donuts. La pallabra toroide tamién s'usa pa referise a un poliedru toroidal, la superficie de revolución xenerada por un polígonu que xira alredor d'una exa.[1]
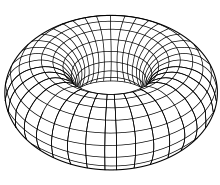
Cuando la curva zarrada ye una circunferencia, la superficie denomina toru. En llinguaxe cotidianu #denominar aniellu al cuerpu que la so superficie esterior ye un toru, lo qu'ilustra la diferencia ente una superficie y el volume zarráu por ella.
Espresión matemática del toroide
[editar | editar la fonte]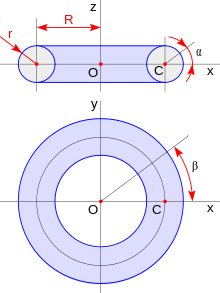
Nun sistema de coordenaes cartesianes de centru O, exes horizontales x y y y exa vertical z, la superficie del toru puede xenerase de la manera siguiente. Constrúyese sobre'l planu xz una circunferencia de radio r con centru nel puntu C que ta sobre la exa x y a distancia R d'O. La superficie del toru xenérase cuando se fai xirar esta circunferencia alredor de la exa z.
Les coordenaes d'un puntu cualesquier del toru llorarse por aciu les siguientes espresiones, onde α ye la llatitú del puntu respeuto del planu xz, y β l'ángulu de rotación de la circunferencia generatriz alredor de la exa z o llargor. Tiense entós que
Espresión paramétrica
[editar | editar la fonte]- x = (R + rcosα)cosβ
- y = (R + rcosα)senβ
- z = rsen α
- ds²= r²dα2 +(R + rcosα)2 dβ2 ; 1ra forma cuadrática
- ; curvadura gausiana [2]
Medidas
[editar | editar la fonte]- Superficie: S = 4π2 Rr = π2 Dd
- Volumen: V = 2π2 Rr² = 0.25π2 Dd²
Ver tamién
[editar | editar la fonte]- Toru (xeometría)
- Ecuaciones de figures xeométriques

