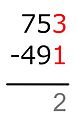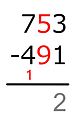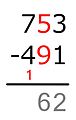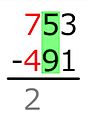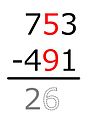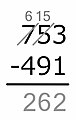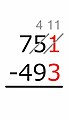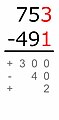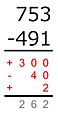Resta

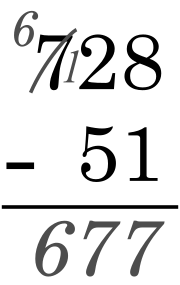


La resta o la sustracción ye una operación d'aritmética que se representa col signu (–), representa la operación d'eliminación d'oxetos d'una coleición. Por casu, na imaxe de la derecha, hai 5-2 mazanes—significando 5 mazanes con 2 quitaes, colo cual hai un total de 3 mazanes. Poro, 5 – 2 = 3. Amás de cuntar frutes, la sustracción tamién puede representar combinación otres magnitúes físicu y astractu usando distintos tipos d'oxetos: númberos negativos, fracciones, númberos irracionales, vectores, decimales, funciones, matrices y más.
La sustracción sigue dellos patrones importantes. Ye anticonmutativa, lo que significa que'l cambéu de la orde camuda'l signu de la respuesta. Nun ye asociativa, lo que significa que cuando se resten más de dos númberos, importa del orde nel que se realiza restar. Restar a 0 nun camuda un númberu. La sustracción tamién obedez a regles predecibles relatives a les operaciones rellacionaes, tales como l'adición y la multiplicación. Toes estes regles pueden probase, a partir de la sustracción de númberos enteros y xeneralizales por aciu los númberos reales y más allá. Les operaciones binaries xenerales que siguen esti patrones estudiar nel álxebra astracta.
Realizar sustracciones ye una de les xeres numbériques más simples. La sustracción de númberos bien pequeños ye accesible pa los neños pequeños. Na educación primaria, los estudiantes enséñase-yos a restar númberos nel sistema decimal, empezando con un solu díxitu y progresivamente encetando problemes más difíciles. Les ayudes mecániques van dende l'antiguu ábaco a l'ordenador moderna.
Resta básica: númberos enteros
[editar | editar la fonte]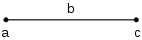
Imaxine un segmentu de recta de llargor b col estremu esquierdu etiquetáu a y l'estremu derechu etiquetáu c. Partiendo d'a, tómase b posiciones a la derecha pa llegar a c. Esti movimientu escontra la derecha modélase matemáticamente por aciu l'adición:
- a + b = c.
De c, tómense b posiciones a la izquierda pa volver a a. Esti movimientu a la izquierda modélase por sustracción:
- c − b = a.

Agora, un segmentu de la llinia marcada colos númberos 1, 2 y 3. Dende la posición 3, nun se toma nengún pasu escontra la esquierda pa permanecer nel 3, polo que 3 − 0 = 3. Precísense 2 pasos a la izquierda pa llegar a la posición 1, polo que 3 − 2 = 1. Esta imaxe ye desaparente pa describir lo qu'asocedería dempués de pasar 3 pasos a la izquierda de la posición 3. Pa representar dicha operación, la llinia tien d'estendese.
Pa restar númberos naturales arbitrarios, unu empieza con una llinia que contién cada númberu natural (0, 1, 2, 3, 4, 5, 6, ...). Del 3, tómase 3 pasos a la izquierda pa llegar a 0, polo que 3 - 3 = 0. Pero 3 − 4 inda ye inválidu, yá que una vegada más sale de la llinia. Los númberos naturales nun son un contestu útil para restar.
La solución ye considerar la llinia numbérica entera (..., −3, −2, −1, 0, 1, 2, 3, ...). Del 3, tómase 4 pasos a la izquierda pa llegar a −1:
- 3 − 4 = −1.
Resta como adición
[editar | editar la fonte]Hai dellos casos onde resta como una operación separada vuélvese problemática. Por casu, 3 - (-2) (esto ye, restar -2 de 3) nun ye darréu resalva dende un puntu de vista del númberu natural o una vista de llinia de númberos, porque nun ta claro de momentu lo que significa mover -2 pasos a la izquierda o pa quitar -2 mazanes. Una solución ye ver a restar como la suma de númberos con signu. Un signu menos extra a cencielles denota inversión aditiva. Entós tenemos 3 - (-2) = 3 + 2 = 5. Esto tamién ayuda a caltener l'aniellu de los enteros "simple" al evitar la introducción de "nuevos" operadores como lu resta. Polo xeneral un aniellu solo tien dos operaciones definíes nel mesmu; nel casu de los númberos enteros, éstos son la suma y la multiplicación. Un aniellu yá tien el conceutu d'inversiones aditivas, pero nun tien nenguna noción d'una operación de sustracción separada, asina que l'usu de la suma como la resta roblada déxanos aplicar los axomes d'aniellu pa restar ensin necesidá de demostrar nada.
Algoritmu de restar
[editar | editar la fonte]Hai dellos algoritmos pa restar, y difieren nel so idoneidad pa diverses aplicaciones. Pal cálculu a mano, afáense un númberu de métodos; por casu, al faer el cambéu, nun se realiza restar real, sinón más bien sigue xubiendo'l cambéu de cuentes.
Pa cálculu en máquina, prefierse'l métodu de complementos, polo que la resta sustituyir por una adición nuna aritmética modular.
La enseñanza de restar nes escueles
[editar | editar la fonte]Los métodos utilizaos pa enseñar restar pa la escuela primaria varien de país en país, y dientro d'un país, tán de moda distintes métodos en distintos momentos.
Delles escueles europees empleguen un métodu de sustracción llamáu métodu austriacu, tamién conocíu como'l métodu d'amiestes. Nesti métodu, nun hai préstamu. Sicasí, esisten muletes (marques p'ayudar a la memoria), que varien d'alcuerdu al país.[1][2]
Esti métodu dixebra la sustracción como un procesu de sustracciones d'un díxitu por valor de posición. A partir d'un díxitu menos significativu, una sustracción de sustraendo:
- sj sj−1 ... s1
dende'l minuendu : mk mk−1 ... m1, onde cada si y mi ye un díxitu, dando en escribir embaxo m1 − s1, m2 − s2, y asina socesivamente, siempres y cuando si nun entepase mi. En casu contrariu, mi amontar en 10 y dellos otros díxitos modificar pa correxir d'esti aumentu. El métodu americanu correxir intentando menguar el díxitu minuendu mi+1 por unu (o siguir el préstamu escontra la esquierda hasta que nun sía un díxitu distintu de cero dende'l qu'empresta). El métodu européu corrixe amontáu'l díxitu sustraendo si+1 por unu.
Exemplu: 704 − 512.
El minuendu ye 704, el sustraendo ye 512. Los díxitos del minuendu son m3 = 7, m2 = 0 y m1 = 4. Los díxitos sustraendo son s3 = 5, s2 = 1 y s1 = 2. Empezando nel llugar de les unidaes, 4 ye non menos de 2 polo que s'escribe 2 la diferencia nel llugar de la resultancia. Nel llugar de les decenes, 0 ye menor que 1, polo que'l 0 amontar en 10, y la diferencia con 1, que ye 9, escribir en llugar de les decenes. El métodu americanu corrixe l'aumentu de diez amenorgando'l díxitu nel llugar de la centena del minuendu n'unu. Esto ye, el 7 ta tacháu y sustitúyese por un 6. Entós, restar procede nel llugar de les centenes, onde 6 nun ye inferior a 5, lo que la diferencia amenorgar nel llugar de la resultancia de cien. Agora terminemos, la resultancia ye 192.
El métodu austriacu nun amenorga la 7 a 6. Más bien aumenta'l díxitu de les centenes del sustraendo n'unu. Faise una pequeña marca cerca o per debaxo d'esta cifra (dependiendo de la escuela). De siguío, restar procede por preguntar qué númberu cuando aumenta en 1, y 5, añader a la mesma, fai 7. La respuesta ye 1, y anótase la resultancia nel llugar de les centenes.
Hai una sotileza adicional en que l'estudiante siempres emplega una tabla de sustracción mental nel métodu americanu. Munches vegaes, el métodu austriacu afala al estudiante a usar mentalmente la tabla de sumar a la inversa. Nel exemplu anterior, en llugar de la adición de 1 a 5, consiguiendo 6, y resta esti dende'l 7, l'estudiante pídese-y que considere qué númberu, cuando aumenta en 1, y 5, añader al mesmu, faciendo 7.
Resta cola mano
[editar | editar la fonte]Métodu austriacu
[editar | editar la fonte]Exemplu:
-
1 + … = 3
-
escribe la diferencia debaxo de la llinia.
-
9 + … = 5
¡La suma riquida (5) ye demasiáu pequeña! -
Poro, añadimos 10 a la mesma y ponemos un 1 sol siguiente llugar más altu nel sustraendo.
-
9 + … = 15
Agora podemos ver la diferencia como antes. -
(4 + 1) + … = 7
-
escribe la diferencia debaxo de la llinia.
-
escribe la diferencia total.
Sustracción d'esquierda a derecha
[editar | editar la fonte]Exemplu:
-
7 − 4 = 3
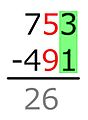
Esta resultancia solo dibúxase con llapiceru equí. -
Por cuenta de que el siguiente díxitu del minuendu ye menor que'l sustraendo, réstase unu del nuesu con llapiceru-en-númberu y mentalmente añader diez a la siguiente.
-
15 − 9 = 6
-
Por cuenta de que el siguiente díxitu del minuendu nun ye menor que'l sustraendo, caltiénse esti númberu.
-
3 − 1 = 2
Métodu americanu
[editar | editar la fonte]Nesti métodu, cada díxitu del sustraendo sustraer del díxitu percima d'él empezando de derecha a esquierda. Si'l númberu cimeru ye demasiáu pequeñu pa restar el númberu inferior del mesmu, sumir 10 al mesmu; esti 10 ye 'emprestáu' dende'l díxitu cimeru escontra la esquierda, lo que se resta 1 de. Depués pásase a restar el siguiente díxitu y el préstamu como sía necesariu, hasta que se restara cada díxitu. Exemplu:
-
3 − 1 = …
-
escribe la diferencia debaxo de la llinia.
-
5 − 9 = …
¡El minuendu (5) ye demasiáu pequeñu! -
Poro, sumir 10 al mesmu. El 10 ye 'emprestáu' del díxitu de la esquierda, que baxa en 1.
-
15 − 9 = …
Agora restar funciona, y escribimos la diferencia debaxo de la llinia. -
6 − 4 = …
-
escribe la diferencia debaxo de la llinia.
-
La diferencia total.
Primeru comerciu
[editar | editar la fonte]Una variante del métodu americanu, onde tolos préstamos realícense primero que toa resta.[3]
Exemplu:
-
1 − 3 = nun ye posible.
Añadimos un 10 al 1. Por cuenta de que el 10 ye "emprestáu" dende'l 5 cercanu, el 5 baxar en 1. -
4 − 9 = nun ye posible.
Asina se procede como nel pasu 1. -
Trabayando de derecha a esquierda:
11 − 3 = 8 -
14 − 9 = 5
-
6 − 4 = 2
Diferencies parciales
[editar | editar la fonte]El métodu de les diferencies parciales estremar d'otros métodos de sustracción verticales porque nengún préstamu o o acarretu realízase. Nel so llugar, úsense unos llugares más o signos de menos en función de si'l minuendu ye mayor o menor que'l sustraendo. La suma de les diferencies parciales ye la diferencia total.[4]
Exemplu:
-
El númberu menor restar del mayor:
700 − 400 = 300
Por cuenta de que el minuendu ye mayor que'l sustraendo, esta diferencia tien un signu de más. -
El númberu menor restar del mayor:
90 − 50 = 40
Por cuenta de que el minuendu ye menor que'l sustraendo, esta diferencia tien un signu de menos. -
El númberu menor restar del mayor:
3 − 1 = 2
Por cuenta de que el minuendu ye mayor que'l sustraendo, esta diferencia tien un signu de más. -
+ 300 − 40 + 2 = 262
Métodos non verticales
[editar | editar la fonte]Cuntando para enriba
[editar | editar la fonte]En llugar d'atopar estrema díxitu per díxitu, puede cuntar los númberos ente'l sustraendo y el minuendu.[5]
Exemplu:
1234 − 567 = pue ser atopada nos siguientes pasos:
- 567 + 3 = 570
- 570 + 30 = 600
- 600 + 400 = 1000
- 1000 + 234 = 1234
Súmase'l valor de cada pasu pa llograr la diferencia total: 3 + 30 + 400 + 234 = 667.
Rompiendo restar
[editar | editar la fonte]Otru métodu que ye útil pal cálculu mental ye estremar restar en pequeños pasos.[6]
Exemplu:
1234 − 567 = puede ser resuelta de la siguiente manera:
- 1234 − 500 = 734
- 734 − 60 = 674
- 674 − 7 = 667
Igual camudo
[editar | editar la fonte]El mesmu métodu de cambéu basar nel fechu de que sumar o restar el mesmu númberu del minuendu y sustraendo nun camuda la respuesta. Añadir la cantidá necesaria pa llograr ceros nel sustraendo.
Exemplu:
«1234 − 567 =» puede ser resuelta de la siguiente manera:
- 1234 − 567 = 1237 − 570 = 1267 − 600 = 667
Unidaes de midida
[editar | editar la fonte]Al restar dos númberos con unidaes de midida, tales como kilogramos o llibres, tienen de tener la mesma unidá. Na mayoría de casos, la diferencia va tener la mesma unidá que los númberos orixinales.
Una esceición ye cuando se resten dos númberos con porcentaxe como unidá. Nesti casu, la diferencia va tener puntos porcentuales como unidá; la diferencia ye que los porcentaxes tienen de ser positivos, ente que los puntos porcentuales pueden ser negativos.
Ver tamién
[editar | editar la fonte]Referencies
[editar | editar la fonte]- ↑ Klapper 1916, p. 177-.
- ↑ David Eugene Smith (1913). The Teaching of Arithmetic (n'inglés). Ginn, páx. 77–.
- ↑ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Trade First
- ↑ Resta de Diferencies Parciales (n'inglés) ; Les munches maneres de l'aritmética en Matemátiques diaries UCSMP Sustracción: Diferencies parciales
- ↑ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Counting Up
- ↑ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Left to Right Subtraction
Enllaces esternos
[editar | editar la fonte]- Plantía:Springer
- Printable Worksheets: Subtraction Worksheets, One Digit Subtraction, Two Digit Subtraction, y ChapterID=1273&CurriculumID=3&Method=Worksheet&NQ=24&NQ4P=3 Four Digit Subtraction (n'inglés)
- Subtraction Game en cut-the-knot (n'inglés)
- Escoyíu de Abacus escoyíu de Abacus y el Misteriu del Bead (n'inglés)