Diferencies ente revisiones de «Efeutu Coriolis»
m iguo fórmula |
m iguo fórmula |
||
| Llinia 135: | Llinia 135: | ||
La Tierra xira muncho más amodo qu'un carrusel. La so velocidá angular ye de <math>\scriptstyle{2\pi}</math> radianes por [[día sideral]] (23 h, 56 m, 4,1 s) ye dicir <math>\scriptstyle{7{,}292\,10^{-5}}\, rad/s</math>. L'aceleración de Coriolis por cuenta de la rotación de la Tierra ye enforma menor. |
La Tierra xira muncho más amodo qu'un carrusel. La so velocidá angular ye de <math>\scriptstyle{2\pi}</math> radianes por [[día sideral]] (23 h, 56 m, 4,1 s) ye dicir <math>\scriptstyle{7{,}292\,10^{-5}}\, rad/s</math>. L'aceleración de Coriolis por cuenta de la rotación de la Tierra ye enforma menor. |
||
Cuando un cuerpu sigue una trayectoria norte-sur sobre la Tierra (siguiendo un meridianu), la componente radial de la so velocidá (la velocidá a la cual el cuerpu avérase o s'alloñar de la exa de rotación terrestre) depende de la [[llatitú]] del cuerpu. Ye fácil ver que la componente radial ye <math>\scriptstyle{V_r=V_{NS}\sin(\mathrm{llatitú})}</math>. Cuando'l cuerpu ta cerca del ecuador, la so distancia respecto a la exa de la Tierra nun camuda. Si la trayectoria del cuerpu ye esti oeste y sigue un [[paralelu]], la so distancia respecto a la exa terrestre nun varia, pero yá vimos que va sentir una aceleración de Coriolis empobinada escontra la exa de la Tierra que vale <math>\scriptstyle{a_{exa}=2\omega V_{EO}}</math>. La componente paralela a la superficie de la Tierra depende de la [[llatitú]] y ye: <math>\scriptstyle{a_c=2\omega V_{EO}\ |
Cuando un cuerpu sigue una trayectoria norte-sur sobre la Tierra (siguiendo un meridianu), la componente radial de la so velocidá (la velocidá a la cual el cuerpu avérase o s'alloñar de la exa de rotación terrestre) depende de la [[llatitú]] del cuerpu. Ye fácil ver que la componente radial ye <math>\scriptstyle{V_r=V_{NS}\sin(\mathrm{llatitú})}</math>. Cuando'l cuerpu ta cerca del ecuador, la so distancia respecto a la exa de la Tierra nun camuda. Si la trayectoria del cuerpu ye esti oeste y sigue un [[paralelu]], la so distancia respecto a la exa terrestre nun varia, pero yá vimos que va sentir una aceleración de Coriolis empobinada escontra la exa de la Tierra que vale <math>\scriptstyle{a_{exa}=2\omega V_{EO}}</math>. La componente paralela a la superficie de la Tierra depende de la [[llatitú]] y ye: <math>\scriptstyle{a_c=2\omega V_{EO}\sin(\mathrm{llatitú})}</math>. |
||
Vemos que nos dos casos, vistu dende la Tierra, un cuerpu que se mueve sobre la superficie de la Tierra siente una aceleración llateral de valor <math>\scriptstyle{a_c=2\omega V\ |
Vemos que nos dos casos, vistu dende la Tierra, un cuerpu que se mueve sobre la superficie de la Tierra siente una aceleración llateral de valor <math>\scriptstyle{a_c=2\omega V\sin(\mathrm{llatitú})}</math> empobinada escontra la derecha de la velocidá. |
||
Un cuerpu que se mueve con una velocidá de 1 m/s, ensin interacción col suelu, a una llatitú de 45° atopa una aceleración llateral de Coriolis igual a: |
Un cuerpu que se mueve con una velocidá de 1 m/s, ensin interacción col suelu, a una llatitú de 45° atopa una aceleración llateral de Coriolis igual a: |
||
{{ecuación| |
{{ecuación| |
||
<math> a_c = 2\cdot 7{,}292\cdot 10^{-5}\ |
<math> a_c = 2\cdot 7{,}292\cdot 10^{-5}\sin(45^\circ) = 1{,}03\cdot 10^{-4} \mathrm{m/s}^2</math>, ||left}} |
||
lo cual correspuende a una fuerza llateral aprosimao 100 000 vegaes menor qu'el so propiu pesu. Dicho otra manera, la trayectoria esviar escontra la derecha como si'l terrén tuviera inclináu escontra la derecha 1 milímetru cada 100 metros. |
lo cual correspuende a una fuerza llateral aprosimao 100 000 vegaes menor qu'el so propiu pesu. Dicho otra manera, la trayectoria esviar escontra la derecha como si'l terrén tuviera inclináu escontra la derecha 1 milímetru cada 100 metros. |
||
| Llinia 147: | Llinia 147: | ||
Si tratar d'un avión que la so velocidá ye 900 km/h (250 m/s), l'aceleración va ser 250 vegaes mayor. L'efectu va ser da-y al avión una trayectoria circular de 4850 km de diámetru (a una llatitú de 45°): |
Si tratar d'un avión que la so velocidá ye 900 km/h (250 m/s), l'aceleración va ser 250 vegaes mayor. L'efectu va ser da-y al avión una trayectoria circular de 4850 km de diámetru (a una llatitú de 45°): |
||
{{ecuación| |
{{ecuación| |
||
<math> a_c=2\omega V\ |
<math> a_c=2\omega V\sin(45^\circ)=\textstyle{V^2\over R} </math> |
||
||left}} |
||left}} |
||
{{ecuación| |
{{ecuación| |
||
<math> 2R= \textstyle{V\over\omega\ |
<math> 2R= \textstyle{V\over\omega\sin(45^\circ)}=\textstyle{250\over 7{,}292\cdot 10^{-5}\sin(45^\circ) }=4{,}846\cdot 10^6\ \mathrm{m}</math> |
||
||left}} |
||left}} |
||
De xacíu, el pilotu va correxir esta esviación, pero nun paez posible que pueda estremala de los efectos del vientu o de los erros de reglaje de la posición neutra de los alerones de dirección y de fondura. |
De xacíu, el pilotu va correxir esta esviación, pero nun paez posible que pueda estremala de los efectos del vientu o de los erros de reglaje de la posición neutra de los alerones de dirección y de fondura. |
||
| Llinia 157: | Llinia 157: | ||
Tomemos el casu d'un [[obús]], asitiáu a una llatitú de 45° y que tira un proyectil a 110 km de distancia. L'ángulu de tiru pa esa distancia ye de 45°. Si desprecia l'efectu de les esfregadures col aire, la velocidá horizontal del proyectil ye de 734 m/s, y el tiempu de vuelu ye de 150 segundos. L'aceleración de Coriolis va ser: |
Tomemos el casu d'un [[obús]], asitiáu a una llatitú de 45° y que tira un proyectil a 110 km de distancia. L'ángulu de tiru pa esa distancia ye de 45°. Si desprecia l'efectu de les esfregadures col aire, la velocidá horizontal del proyectil ye de 734 m/s, y el tiempu de vuelu ye de 150 segundos. L'aceleración de Coriolis va ser: |
||
{{ecuación| |
{{ecuación| |
||
<math> a_c=2\omega V\ |
<math> a_c=2\omega V\sin(\mathrm{llatitú})=7{,}58\cdot 10^{-2}\ \mathrm{m/s}^2 </math> |
||
||left}} |
||left}} |
||
La distancia llateral d'esviadura provocada pola aceleración de Coriolis ye: |
La distancia llateral d'esviadura provocada pola aceleración de Coriolis ye: |
||
Revisión a fecha de 12:30 3 may 2018

Esquierda: El movimientu reparáu dende un puntu de vista esternu.
Derecha: El movimientu vistu dende un puntu de vista solidariu col sistema non inercial.
El efectu Coriolis, descritu en 1836 pol científicu francés Gaspard-Gustave Coriolis, ye l'efectu que se repara nun sistema de referencia en rotación cuando un cuerpu atópase en movimientu respecto de dichu sistema de referencia. Esti efectu consiste na esistencia d'una aceleración relativa del cuerpu en dichu sistema en rotación. Esta aceleración ye siempres perpendicular a la exa de rotación del sistema y a la velocidá del cuerpu.
L'efectu Coriolis fai qu'un oxetu que se mueve sobre'l radiu d'un discu en rotación tienda a acelerase con al respective de esi discu según si'l movimientu ye escontra la exa de xiru o alloñar d'ésti. Pol mesmu principiu, nel casu d'una esfera en rotación, el movimientu d'un oxetu sobre los meridianos tamién presenta esti efectu, yá que dichu movimientu amenorga o amonta la distancia respecto a la exa de xiru de la esfera.
Por cuenta de que l'oxetu sufre una aceleración dende'l puntu de vista del observador en rotación, ye como si pa ésti esistiera una fuerza sobre l'oxetu que lu acelera. A esta fuerza llámase-y fuerza de Coriolis, y nun ye una fuerza real nel sentíu de que nun hai nada que la produza. Trátase pos d'una fuerza inercial o ficticia, que s'introduz pa esplicar, dende'l puntu de vista del sistema en rotación, l'aceleración del cuerpu, que'l so orixe ta en realidá, nel fechu de que'l sistema d'observación ta rotando.
Un exemplu canónicu d'efectu Coriolis ye l'esperimentu imaxinariu nel que disparamos un proyectil dende l'Ecuador en dirección norte. El cañón ta xirando cola tierra escontra l'este y, por tanto, imprime al proyectil esa velocidá (amás de la velocidá escontra alantre al momentu de la impulsión). Al viaxar el proyectil escontra'l norte, sobrevuela puntos de la tierra que la so velocidá llineal escontra l'este va menguando cola llatitú creciente. La inercia del proyectil escontra l'este fai que la so velocidá angular aumente y que, por tanto, alantre a los puntos que sobrevuela. Si'l vuelu ye abondo llargu (ver cálculos a la fin del artículu), el proyectil va cayer nun meridianu asitiáu al este d'aquél dende'l cual disparóse, a pesar de que la dirección del disparu foi esactamente escontra'l norte. Finalmente, l'efectu Coriolis, al actuar sobre mases d'aire (o agua) en llatitúes entemedies, induz un xiru al esviar escontra l'este o escontra l'oeste les partes d'esa masa que ganen o pierdan llatitú o altitú nel so movimientu.
Introducción

La fuerza de Coriolis ye una fuerza ficticio qu'apaez cuando un cuerpu ta en movimientu con al respective de un sistema en rotación y descríbese el so movimientu nesi referencial. La fuerza de Coriolis ye distinta de la fuerza centrífugo. La fuerza de Coriolis siempres ye perpendicular a la dirección de la exa de rotación del sistema y a la dirección del movimientu del cuerpu vista dende'l sistema en rotación. La fuerza de Coriolis tien dos componentes:
- una componente tanxencial, debida a la componente radial del movimientu del cuerpu, y
- una componente radial, debida a la componente tanxencial del movimientu del cuerpu.
La componente del movimientu del cuerpu paralela a la exa de rotación nun nicia fuerza de Coriolis. El valor de la fuerza de Coriolis ye:
onde:
- ye la masa del cuerpu.
- ye la velocidá del cuerpu nel sistema en rotación .
- ye la velocidad angular del sistema en rotación vista dende un sistema inercial.
- indica productu vectorial.
Hestoria
En 1835, Gaspard-Gustave de Coriolis, nel so artículu Sur -yos équations du mouvement relatif deas systèmes de corps,[1] describió matemáticamente la fuerza que terminó llevando'l so nome. Nesi artículu, la fuerza de Coriolis apaez como una componente suplementaria a encomalo centrífuga esperimentada por un cuerpu en movimientu relativu a un referencial en rotación, como puede producise, por casu, nos engranajes d'una máquina. El razonamientu de Coriolis basábase sobre un analís del trabayu y de la enerxía potencial y cinética nos sistemes en rotación. Agora, la demostración más utilizada pa enseñar la fuerza de Coriolis utiliza les ferramientes de la cinemática.
Esta fuerza nun empezó a apaecer na lliteratura meteorolóxico y oceanográfico hasta finales del sieglu XIX. El términu fuerza de Coriolis apaeció a principios del sieglu XX.
Formulación y demostración
Pa demostrar la espresión analítica espresada na introducción, pueden usase dos aproximaciones distintes: por caltenimientu del momentu angular o por derivación en base móvil. De siguío esplíquense dambes.
Demostración per caltenimientu del momentu angular

Ye precisu recordar que cuando un observador nun sistema non inercial (como lo ye un sistema en rotación) trata d'entender el comportamientu del so sistema como si fora un sistema inercial ve apaecer fuerces ficticies. Nel casu d'un sistema en rotación, l'observador ve que tolos oxetos que nun tán suxetos alloñar de manera radial como si actuara sobre ellos una fuerza proporcional a les sos mases y a la distancia a una cierta recta (la exa de rotación). Esa ye la fuerza centrífugo qu'hai que compensar cola fuerza centrípeto pa suxetar los oxetos. De xacíu, pa un observador esternu, asitiáu nun sistema inercial (sistema fixu), la única fuerza qu'esiste ye la fuerza centrípeto, cuando los oxetos tán suxetos. Si nun lu tán, los oxetos van tomar la tanxente y van alloñase de la exa de rotación.
Si los oxetos nun tán inmóviles con respectu al observador del sistema en rotación, otra fuerza ficticio apaez: la fuerza de Coriolis. Vistu dende'l sistema en rotación, el movimientu d'un oxetu puede descomponese nuna componente paralela a la exa de rotación, otra componente radial (asitiada sobre una llinia que pasa pela exa de rotación y perpendicular a ésti), y una tercera componente tanxencial (tanxente a un círculu centráu na exa y perpendicular a ésti) (ver gráfica).
Un oxetu que se mueve paralelamente a la exa de rotación, vistu d'un sistema fixu, xira col sistema en rotación a la mesma velocidad angular y con radio constante. La única fuerza qu'actúa sobre l'oxetu ye la fuerza centrípeto. L'observador del sistema en rotación namái nota la fuerza centrífugo contra la cual hai qu'oponese por que se quede a la mesma distancia de la exa.

Supóngase qu'un observador nel sistema en rotación caltién una masa a una distancia de la exa de rotación por aciu un filo de masa despreciable. L'observador tira del filo y modifica llixeramente'l radiu de rotación de la masa de . Eso tomó-y un tiempu . Como'l momentu dinámicu ye nulu, el momentu angular de la masa caltiense. Si ye la velocidá de la masa, el caltenimientu del momentu angular espresa:
El signu menos indica que cuando'l radiu aumenta la velocidá tanxencial mengua.
Si la masa moviérase siguiendo una trayectoria radial, afita con respectu al sistema en rotación, calteniendo en consecuencia la mesma velocidad angular del sistema en rotación, la so velocidá llineal aumentaría de (o menguáu, si ye negativu). Pa un observador fixu, ente la velocidá de la masa que se ve obligada a siguir una trayectoria radial y la velocidá de la masa que caltién el so momentu angular hai una diferencia de:
Como l'oxetu nun ta suxetu al sistema en rotación, l'observador nesi sistema ve la masa tomar una velocidá llateral . Eso interprétase como l'aplicación d'una fuerza llateral (de Coriolis). Si'l cambéu de velocidá tomó segundos, l'aceleración de Coriolis va ser (en valor absolutu):
- ,
onde ye la velocidá radial. Esa aceleración correspuende a una fuerza (de Coriolis) de:
Considerando un oxetu con velocidá tanxencial vista pol observador nel sistema en rotación. Esta vegada, la mesma masa tenida por un filo tien una velocidá angular distintu del sistema en rotación. Pal observador nel sistema en rotación, les fuerces que nota aplicaes a la masa por que siga una trayectoria circular son: la fuerza centrífugo que ve aplicada en tolos oxetos, más la fuerza centrípeto por cuenta de la rotación aparente de la masa . Pero eso non basta. Hai entá otra fuerza aparente, y ye precisamente la fuerza de Coriolis. Calcúlase agora la fuerza centrípeto que ve un observador fixu: la velocidá tanxencial ye . Pa esti observador, la fuerza centrípeto que caltién la masa a distancia constante va ser:
El primer términu ye la fuerza centrífugo común a tolos oxetos que xiren col sistema en rotación. El terceru ye la fuerza centrípeto debida a la rotación de la masa con respectu al sistema en rotación. Y el segundu términu ye la fuerza de Coriolis. Ye un términu suplementariu debíu al fechu de que la fuerza centrípeto depende del cuadráu de la velocidá tanxencial y nun puede llograse sumando les fuerces centrífugo y centrípeto por cuenta de velocidaes parciales. La fuerza de Coriolis ye:
Como se dixo , esa fuerza ye radial.
Demostración pola derivación en base móvil
Pa esta demostración utilizará'l subíndice abs pa indicar magnitúes vistes dende'l sistema de referencia inercial, esto ye, unu onde l'espaciu sía homoxéneu y isótropo y onde el tiempu sía constante. El subíndice rel (relativa) referir a magnitúes vistes dende una referencia non galileana o non inercial. El subíndice ar (arrastre) fai referencia al movimientu de la base móvil al respective de la base fixa. Tamién ye necesariu conocer cómo se deriva nuna base móvil:
Una aceleración ye un cambéu na magnitú o na orientación de la velocidá respecto del tiempu. Pa esa demostración considérase un movimientu que nun varia la magnitú de la so velocidá, esto ye, que nun ta sometíu a fuerces que tengan dalguna componente na dirección del movimientu. Entós:
Per una parte:
Por otra:
onde:
Como nun se considera'l movimientu alredor del Sol, sinón namái'l xiru de la tierra en redol a sigo mesma:
Amás, como se ta imaxinando un movimientu ensin aceleración relativa (como'l d'un proyectil):
quedando asina:
Pero:
Entós:
Volviendo de primeres:
L'aceleración de Coriolis ye'l primera sumando:
L'aceleración centrípeta ye'l segundu:
Meteoroloxía, oceanografía y fuerza de Coriolis
L'exemplu más vultable de manifestación del efectu Coriolis dase cuando mases d'aire o d'agua muévense siguiendo meridianos terrestres, y la so trayectoria y velocidá vense modificaes por él.[2] N'efectu, los vientos o corrientes oceániques que se mueven siguiendo un meridianu esviar acelerando na dirección de xiru (esti) si van escontra los polos o al contrariu (oeste) si van escontra l'ecuador. Puede añedir, que por consecuencia, nel Ecuador, nun hai efectu de Coriolis. La manifestación d'estes esviaciones produz, de manera análoga al xiru de la bolina amosáu de primeres, que les umbaes tiendan a xirar nel hemisferiu sur nel sentíu de les aguyes del reló y, nel hemisferiu norte, en sentíu contrariu.
L'efectu de la fuerza de Coriolis tendrá de considerase siempres que s'estudie'l movimientu de fluyíos y tamién el de cualquier oxetu móvil sobre esferes o superficies planes en rotación. Esto inclúi a los planetes gaseosos del sistema solar, el Sol y toles estrelles y, nel planeta Tierra, el movimientu de les agües de los ríos, los llagos, los océanos y, poques gracies, de la atmósfera. L'efectu de Coriolis prediz que siempres que se reparen los movimientos xiratorios d'esos cuerpos, los vórtices van siguir la norma descrita pa les umbaes y anticiclones terrestres.[3]
Amás de la so influencia sobre l'atmósfera, ye bien vultable la que tien tamién sobre la circulación oceánica. Nes cuenques que tienen la forma apropiada (como, por casu, la cuenca del Atlánticu norte y la del Atlánticu sur), l'efectu Coriolis esvia a les corrientes marines escontra la derecha nel hemisferiu norte y escontra la esquierda nel hemisferiu sur, de la mesma manera qu'asocede cola circulación xeneral de los vientos.
Les esceiciones o cambeos d'esti patrón xeneral de la circulación xeneral de los océanos tienen que ver cola disposición de les mariñes y la compensación introducida poles corrientes templaes que van, nos océanos, de les mariñes orientales de la zona intertropical escontra les occidentales de les zones templaes de los continentes (corriente del Golfu y de Kuro Shivo, especialmente). Amás, nos océanos, lo mesmo qu'asocede na atmósfera, produzse una especie de converxencia nes llatitúes ecuatoriales pola fuerza centrífuga del movimientu de rotación: tanto l'océanu como l'atmósfera tienen un abombadura ecuatorial pola rotación terrestre, de dellos kilómetros d'altor nel casu de los océanos y entá mayor nel casu de l'atmósfera por cuenta de la so menor densidá. De la mesma, esti "abombadura" causa una especie de torga a la llibre circulación y al llibre intercambiu d'enerxía (oceánica y atmosférica) ente los dos hemisferios. La circulación na zona ecuatorial ye, poro, d'este a oeste, tantu no que fai a les corrientes ecuatoriales del norte y del sur como con al respective de los alisios del nordés nel hemisferiu norte y del sureste nel hemisferiu sur. A lo último, lo que se denominó abombadura ecuatorial de los océanos tien delles consecuencies: ente elles, la formación de lo que se denominó contracorrientes ecuatoriales tamién del norte y del sur, definíes ya identificaes en munchos atles y llibros de xeografía y de ciencies de la Tierra, y l'esviación escontra les zones subtropical y templar: de nuevu, escontra la derecha nel hemisferiu norte y escontra la esquierda nel hemisferiu sur.
Efectos de la fuerza de Coriolis
Una de les rares ocasiones na cual una persona puede sentir la fuerza de Coriolis ye cuando trata de caminar siguiendo una trayectoria radial nun tiovivo (o carrusel). Cuando la persona alloñar de la exa de rotación, va sentir una fuerza que lo emburria nel sentíu contrariu a la rotación: ye la fuerza de Coriolis.[4] Cuando una persona allóñase o s'avera de la exa de rotación a una velocidá de 1 m/s nun tiovivo que xira a 10 vueltes per minutu, l'aceleración de Coriolis ye:
Trátase, poro, d'una aceleración llateral 4,6 vegaes más pequena que la gravedá, pero que pa una persona de 70 kg, eso correspuende a una fuerza llateral igual al pesu de 15 kg. que ye perfectamente percibida.
Oxetos que se mueven sobre la Tierra
La Tierra xira muncho más amodo qu'un carrusel. La so velocidá angular ye de radianes por día sideral (23 h, 56 m, 4,1 s) ye dicir . L'aceleración de Coriolis por cuenta de la rotación de la Tierra ye enforma menor.
Cuando un cuerpu sigue una trayectoria norte-sur sobre la Tierra (siguiendo un meridianu), la componente radial de la so velocidá (la velocidá a la cual el cuerpu avérase o s'alloñar de la exa de rotación terrestre) depende de la llatitú del cuerpu. Ye fácil ver que la componente radial ye Fallu al revisar la fórmula (MathML con alternativa SVG o PNG (recomendau en restoladores y ferramientes d'accesibilidá modernos): Respuesta inválida ("Math extension cannot connect to Restbase.") dende'l sirvidor "http://localhost:6011/ast.wikipedia.org/v1/":): {\displaystyle \scriptstyle{V_r=V_{NS}\sin(\mathrm{llatitú})}} . Cuando'l cuerpu ta cerca del ecuador, la so distancia respecto a la exa de la Tierra nun camuda. Si la trayectoria del cuerpu ye esti oeste y sigue un paralelu, la so distancia respecto a la exa terrestre nun varia, pero yá vimos que va sentir una aceleración de Coriolis empobinada escontra la exa de la Tierra que vale . La componente paralela a la superficie de la Tierra depende de la llatitú y ye: Fallu al revisar la fórmula (error de sintaxis): {\displaystyle \scriptstyle{a_c=2\omega V_{EO}\sin(\mathrm{llatitú})}} .
Vemos que nos dos casos, vistu dende la Tierra, un cuerpu que se mueve sobre la superficie de la Tierra siente una aceleración llateral de valor Fallu al revisar la fórmula (error de sintaxis): {\displaystyle \scriptstyle{a_c=2\omega V\sin(\mathrm{llatitú})}} empobinada escontra la derecha de la velocidá.
Un cuerpu que se mueve con una velocidá de 1 m/s, ensin interacción col suelu, a una llatitú de 45° atopa una aceleración llateral de Coriolis igual a:
,
lo cual correspuende a una fuerza llateral aprosimao 100 000 vegaes menor qu'el so propiu pesu. Dicho otra manera, la trayectoria esviar escontra la derecha como si'l terrén tuviera inclináu escontra la derecha 1 milímetru cada 100 metros.
Si tratar d'un avión que la so velocidá ye 900 km/h (250 m/s), l'aceleración va ser 250 vegaes mayor. L'efectu va ser da-y al avión una trayectoria circular de 4850 km de diámetru (a una llatitú de 45°):
De xacíu, el pilotu va correxir esta esviación, pero nun paez posible que pueda estremala de los efectos del vientu o de los erros de reglaje de la posición neutra de los alerones de dirección y de fondura.
Balística
Tomemos el casu d'un obús, asitiáu a una llatitú de 45° y que tira un proyectil a 110 km de distancia. L'ángulu de tiru pa esa distancia ye de 45°. Si desprecia l'efectu de les esfregadures col aire, la velocidá horizontal del proyectil ye de 734 m/s, y el tiempu de vuelu ye de 150 segundos. L'aceleración de Coriolis va ser:
Fallu al revisar la fórmula (error de sintaxis): {\displaystyle a_c=2\omega V\sin(\mathrm{llatitú})=7{,}58\cdot 10^{-2}\ \mathrm{m/s}^2 }
La distancia llateral d'esviadura provocada pola aceleración de Coriolis ye:
Esa distancia correspuende a un erru nel ángulu de tiru de 0,44°. Les opiniones diverxen sobre la importancia d'esti erru, comparáu cola influencia d'otres fuerces y, sobremanera, cola fuerza provocada pol efectu Magnus sobre proyectiles que xiren axialmente.
Pa cañones de menor algame, l'erru nel ángulu de tiru ye entá menor. Por casu, pa un proyectil que'l so algame ye de 20 km y que la so velocidá media ye la mesma, l'erru del ángulu ye 25 vegaes menor.
Efectu Eötvös
La versión simplificada del efectu Coriolis esta amestada al so componente horizontal causada por movimientos horizontales con al respective de la superficie terrestre.
Pero tamién hai componentes verticales del efectu Coriolis que son significativos. Los oxetos que viaxen escontra l'este a gran velocidá van esviase escontra riba (van paecer más llixeros), ente que los que lo faigan escontra l'oeste van esviase escontra baxo (van paecer más pesaos). Esto conozse como'l efectu Eötvös. Esti componente vertical del efectu Coriolis ye mayor nel ecuador, y amenórgase a cero nos polos.
Otru casu a tener en cuenta ye'l d'oxetos que viaxen en dirección perpendicular al planu terrestre. Aquellos que se muevan enriba a gran velocidá van esviar escontra l'oeste y los que lo faigan escontra baxo van esviase escontra l'este. L'efectu de nuevu algama'l so máximu nel ecuador y ye 0 nos polos (nel ecuador un movimientu vertical ye perpendicular a la exa de rotación y nos polos sicasí ye paralelu y polo tanto l'efectu causáu por Coriolis nesi casu ye 0).
Esplicación intuitiva
Imaxinemos un tren que viaxa per una vía ensin rozamiento alredor del ecuador de la Tierra a la velocidá necesaria pa completar una vuelta al mundu nun día (465 m/s).[5] Analizamos l'efectu Coriolis en tres casos:
- 1. Cuando se mueve escontra l'oeste.
- 2. Cuando esta en reposu.
- 3. Cuando se mueve escontra l'este.
Pa cada unu d'estos casos calculamos l'efectu Coriolis, primero dende'l puntu de vista del nuesu sistema de referencia en rotación na Tierra para de siguío comprobar que la resultancia ye'l mesmu reparando'l tren nun sistema de referencia inercial. Na siguiente imaxe podemos reparar los trés casos nel sistema de referencia inercial vistos dende un puntu fixu sobre la tierra na so eje de rotación:

- 1. El tren viaxa escontra l'oeste: Nesti casu'l movimientu ye en dirección contraria a la de rotación, polo tanto nel sistema de referencia en rotación de la tierra'l términu causáu pol efectu Coriolis ta dirixíu escontra la exa de rotación, nel ecuador esto ye escontra baxo, aplicando la fórmula del efectu Coriolis el tren y los sos pasaxeros tendríen de ser más pesaos mientres se mueven escontra l'oeste.
- Si reparamos el tren nel sistema de referencia inercial dende'l puntu fixu sobre'l Polu Norte, reparamos qu'a esa velocidá esti caltiense inmóvil ente que la Tierra rota sol tren, por tantu la única fuerza qu'actúa sobre'l tren ye la gravedá y la fuerza de reacción de les víes. Esta fuerza ye mayor (un 0,34%)[5] que la fuerza total resultante esperimentada pol tren cuando esta en reposu (y rotando xuntu cola Tierra). L'efectu Coriolis dexa esplicar esta diferencia nel nuesu sistema de referencia en rotación.
- 2. El tren párase: Dende'l nuesu puntu de vista na tierra (sistema de referencia en rotación) la velocidá del tren ye 0 y por tantu la fuerza derivada de Coriolis ye tamién 0 polo que tanto'l tren como los sos pasaxeros recuperen el so pesu normal.
- Dende'l puntu de vista fixu sobre la Tierra nel sistema de referencia inercial, el tren xira nesti casu xuntu col restu de la Tierra. Un 0,34 per cientu de la fuerza de la gravedá apurre la fuerza centripeta necesaria pa consiguir el movimientu circular nesi sistema de referencia. El restu de la fuerza que podría midise usando una báscula, causaría que'l tren y los sos pasaxeros fueren más llixeros que nel casu anterior.
- 3. El tren camuda la so dirección y viaxa escontra l'este. Nesti casu al movese na mesma dirección que la rotación terrestre, l'efectu de Coriolis va tar dirixíu pa escontra fora de la exa de rotación, esto ye, escontra riba. Esta fuerza va causar que'l tren y los sos pasaxeros rexistren un menor peso que cuando s'atopaben en reposu.
- Vistu dende l'espaciu, nel sistema de referencia inercial el tren al viaxar escontra l'este va sumar la so velocidá a la de la tierra y por tantu va vese xirando al doble de velocidá que cuando taba en reposu y por tantu la cantidá de fuerza centrípeto necesaria pa caltener el movimientu circular ye mayor amenorgando la fuerza neto actuando sobre les víes escontra'l centru de la tierra. Esta diferencia de fuerza ye la esplicada enantes pol términu de Coriolis en sistema de referencia en rotación.
- Como comprobación final podemos imaxinar al propiu tren como sistema de referencia en rotación. Una y bones el sistema rota al doble de velocidad angular qu'el de la tierra'l componente de fuerza centrífugo en dichu sistema de referencia ye mayor qu'el de la tierra y al tar los pasaxeros en reposu en dichu sistema esti sería l'únicu componente adicional, esplicando de nuevu que'l tren y los sos pasaxeros sían más llixeros que nos dos casos anteriores.
Esto esplica por que los proyectiles a alta velocidá que se disparen escontra l'este esviar escontra riba ente que si son disparaos escontra l'oeste la esviación ye escontra baxo. Esta componente vertical del efectu de Coriolis denominar el Efectu Eötvös.[6]
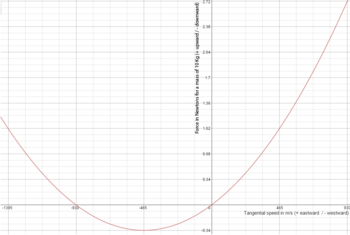
Podemos usar l'exemplu pa esplicar por que el efectu Eötvös empieza a amenorgase n'oxetos que viaxen escontra l'oeste una vegada qu'el so velocidá tanxencial supera la velocidá de rotación de la tierra (465 m/s nel ecuador). Si'l tren que viaxa escontra l'oeste nel exemplu amonta la so velocidá nesa dirección y reparar dende'l sistema de referencia inercial nel espaciu vamos ver qu'empieza a rotar alredor de la tierra que xira debaxo en dirección contraria. Pa caltener esa trayectoria circular, parte de la fuerza de la gravedá qu'emburria al tren contra les víes actuaría como fuerza centrípeto. Una vegada que'l tren doblara la so velocidá a 930 m/s la fuerza centrípeto sería igual a la esperimentada cuando'l tren atópase paráu. Dende'l puntu de vista del sistema de referencia inercial en dambos casos el tren ta rotando a la mesma velocidá (465 m/s) solo qu'en direcciones opuestes. Polo tanto la fuerza ye la mesma y por tantu l'efectu Eötvös atayaríase dafechu a esa velocidá. Cualquier oxetu que se mueva escontra l'oeste a una velocidá cimera a 930 m/s nun esperimentara una esviación escontra baxo, si non escontra riba. El gráficu de la derecha ilustra la fuerza causada pol efectu Eötvös qu'esperimentaría un oxetu de 10 gramos nel tren del exemplu en función de la so velocidá. La forma parabólica del gráficu esplícase porque la fórmula de la fuerza centrípeto ye proporcional al cuadráu de la velocidá tanxencial. Nel sistema de referencia inercial la parte de baxo de la parábola taría centrada nel orixe. El desplazamientu del orixe esplícase porque tamos usando'l sistema de referencia en rotación de la tierra. Reparando'l gráficu podemos comprobar que l'efectu Eötvös nun ye simétricu, y que la fuerza escontra baxo esperimentada por un oxetu viaxando escontra l'oeste a gran velocidá ye menor que la fuerza escontra riba esperimentada pol mesmu oxetu viaxando en dirección al este a la mesma velocidá.
Aplicación práctica
Una aplicación práctica de la fuerza de Coriolis ye'l caudalímetro másico, un preséu que mide'l caudal másico d'un fluyíu que circula al traviés d'una tubería. Esti preséu foi comercializáu en 1977 por Micro Motion Inc.
Los caudalímetros normales miden el caudal volumétrico, que ye proporcional al caudal másico namái cuando la densidá del fluyíu ye constante. Si'l fluyíu tien una variación de densidá o contién burbuyes, entós el caudal volumétrico, multiplicáu pola densidá, nun va ser esactamente igual al caudal másico. El caudalímetro másico de Coriolis funciona aplicando una fuerza de vibración a un tubu curvado al traviés del cual pasa'l fluyíu. L'efectu Coriolis crea una fuerza nel tubu perpendicular a dambes direcciones: la de vibración y la dirección de la corriente. Esta fuerza midir pa llograr el caudal másico. Los caudalímetros de Coriolis pueden usase amás con fluyíos non newtonianos, nos cualos los caudalímetros normales tienden a dar resultancies errónees. El mesmu preséu puede usase pa midir la densidá del fluyíu. Esti preséu tien una novedá adicional, que consiste en que'l fluyíu ta nun tubu llisu, ensin partes móviles, que nun precisa llimpieza nin caltenimientu y presenta una cayida de presión bien baxa.
Ver tamién
- Corriente marina
- Espiral de Ekman
- Maelstrom
- Marea
- Mecanismu de torna rápida
- Pendilexu de Foucault
- Productu vectorial
- Tresporte de Ekman
- Vientos alisios
Referencies
- ↑ Auteur: Gaspard-Gustave de Coriolis. Publication: Deux articles: 1)«Mémoire sur -y principe deas forces vives dans -yos mouvements relatifs deas machines», Journal de l’École polytechnique, v. XIII, cahier XXI (1832), p. 268-302 (Lu à l’Académie deas sciences -y 6 juin 1831 ); 2)«Mémoire sur -yos équations du mouvement relatif deas systèmes de corps», Journal de l’École polytechnique, 24° cahier, XV, cahier XXIV, p. 142-154. Année de publication: 1835. Nome de Pages: 48. Résumé: En deux articles de 1831 et 1835, Coriolis met en évidence la notion de «force d’entraînement» et de «forces centrifuges composées»; ces dernières prendront -y nom de force de Coriolis, permettant d’expliquer -yos phénomènes -yos plus divers de rotation d’un repère par rapport à un autre (pendule de Foucault, mouvements deas masses d’air et d’eau à la surface du globe, etc.).
- ↑ An Intuitive Approach to the Coriolis Effect Kristian Silver. Bachelor Thesis in Meteorology. Department of Earth Sciences, Uppsala University. Testu completu en PDF
- ↑ The Coriolis Effect – a conflict between common sense and mathematics Anders Persson, The Swedish Meteorological and Hydrological Institute, Norrköping, Sweden
- ↑ L'efectu Coriolis. Arquivu PDF. 870 KB 17 páxines. Un discutiniu xeneral pol meteorólogu Anders Persson de diversos aspeutos de la xeofísica, cubriendo l'efectu Coriolis, yá que se toma en cuenta en Meteoroloxía y Oceanografía, l'efectu de Eötvös, el pendilexu de Foucault, y columnes de Taylor
- ↑ 5,0 5,1 Persson, Anders. «The Coriolis Effect – a conflict between common sense and mathematics» (n'inglés). The Swedish Meteorological and Hydrological Institute (Norrköping, Suecia): p. 8. Archivado del original el 6 de setiembre de 2005. https://web.archive.org/web/20050906101226/http://met.no/english/topics/nomek_2005/coriolis.pdf. Consultáu'l 6 de setiembre de 2015.
- ↑ Rugai, Nick (1 d'avientu de 2012). Computational Epistemology: From Reality To Wisdom (n'inglés), páx. 304. ISBN 1300477237.
Bibliografía
- Arthur N. Strahler. Physical Geography. New York, John Wiley & Sons, 1960, 2nd edition. La traducción española ye de 1974.
- Joseph Y. Williams, editor. World Atles. Englewood Cliffs, New Xerséi, Estaos Xuníos: Prentice - Hall Inc., 1963.
Enllaces esternos
 Wikimedia Commons tien conteníu multimedia tocante a Fuerza de Coriolis.
Wikimedia Commons tien conteníu multimedia tocante a Fuerza de Coriolis.- Animaciones interesantes sobre l'efectu Coriolis.















































