Productu vectorial
| Productu vectorial | |
|---|---|
|
operación binaria y vector multiplication (en) | |

En matemátiques, el productu vectorial de Gibbs o producto cruz ye una operación binaria ente dos vectores nun espaciu tridimensional. La resultancia ye un vector perpendicular a los vectores que se multipliquen, y polo tanto normal al planu que los contién. Por cuenta de la so capacidá de llograr un vector perpendicular a otros dos vectores, que'l so sentíu varia d'alcuerdu al ángulu formáu ente estos dos vectores, esta operación ye aplicada con frecuencia pa resolver problemes matemáticos, físicos o d'inxeniería.
Definición[editar | editar la fonte]

Sían dos vectores y nel espaciu vectorial . El productu vectorial ente y da como resultáu un nuevu vector, . El productu vectorial y se denota por aciu , por ello llamar tamién producto cruz. Nos testos manuscritos, pa evitar tracamundios cola lletra x (xe), ye frecuente denotar el productu vectorial por aciu:[1]
El productu vectorial puede definise d'una manera más compacta de la siguiente manera:
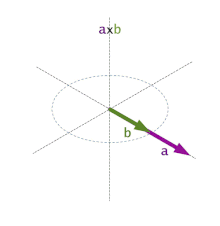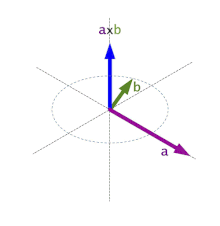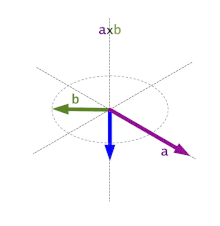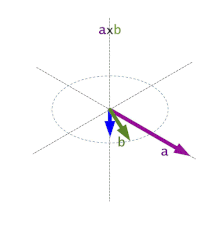
onde ye'l vector unitariu y ortogonal a los vectores a y b y la so direición ta dada pola regla de la mano derecha y θ ye, como antes, l'ángulu ente a y b. A la regla de la mano derecha se la llapada de cutiu tamién regla del sacacorchos.
===Precisiones denominar productu vectorial del vector a pol vector b [2] al vector denotado por y definíu poles trés esixencies siguientes:
- el módulu de ye igual al módulu de a por módulu de b por , onde ye l'ángulu empobináu formáu polos vectores a y b
- el vector ye perpendicular a cada unu de los vectores a y b
- la direición del vector al respective de los vectores a y b ye igual que la de la exa coordenada Oz al respective de les exes coordenaes Ox y Oy, como si xirara de Ox a Oy y avanzara na direición positiva de Oz.
Productu vectorial de dos vectores[editar | editar la fonte]
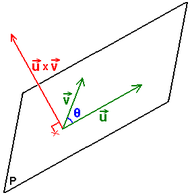
Sían los vectores concurrentes de , l'espaciu allegáu tridimensional según la base anterior. Defínese'l productu:
Onde w ye'l productu vectorial de o y v, definíu asina:
onde la última fórmula interprétase como:
esto ye:
Usando una notación más compacta, por aciu el desenvolvimientu pola primer fila d'un determinante simbólicu d'orde 3 (ye simbólicu porque los términos de la primer fila nun son escalares):
Que da orixe a la llamada regla de la mano derecha o regla del sacacorchos: xirando'l primer vector escontra'l segundu pol ángulu más pequeñu, la direición de ye'l d'un sacacorchos que xire na mesma direición.
Exemplu[editar | editar la fonte]
El productu vectorial de los vectores y calcular de la siguiente manera:
Espandiendo'l determinante:
Dando como resultáu:
Puede verificase fácilmente que ye ortogonal a los vectores y efectuando'l productu escalar y verificando qu'ésti ye nulu (condición de perpendicularidad de vectores)
Propiedaes[editar | editar la fonte]
Identidaes[editar | editar la fonte]
Cualesquier que sían los vectores , y :
- ; el productu vectorial nun ye asociativu #
- ; cancelación por ortogonalidad.
- Si con y , ; l'anulación del productu vectorial apurre la condición de paralelismu ente dos direiciones.
- ; distributividad pela derecha #
; conocida como regla de la espulsión.
- ; conocida como identidá de Jacobi.
- , na espresión del términu de la derecha, sería'l módulu de los vectores y , siendo , l'ángulu menor ente los vectores y ; esta espresión rellaciona al productu vectorial cola área del paralelogramu que definen dambos vectores.
- El módulu o norma del productu vectorial puede calculase fácilmente ensin faer el productu vectorial:
- El vector unitariu ye normal al planu que contién a los vectores y .
- [3]
- ( Asociatividad respectu del factor escalar )
Bases ortonormales y productu vectorial[editar | editar la fonte]
Sía un sistema de referencia nel espaciu vectorial . Dizse que ye una base ortonormal derecha si cumple coles siguientes condiciones:
- ; esto ye, los trés vectores son ortogonales ente sigo.
- ; esto ye, los vectores son vectores unitarios (y poro, dada la propiedá anterior, son ortonormales).
- , , ; esto ye, cumplen la regla de la mano derecha.
Vectores axiales[editar | editar la fonte]
Cuando consideramos dos magnitud físiques vectoriales, el so productu vectorial ye otra mangitud física aparentemente vectorial que tien un estrañu comportamientu al respective de los cambeos de sistema de referencia. Los vectores que presenten eses anomalíes llámense pseudovectores o vectores axiales. Eses anomalíes deber a que non tou ente formáu de trés componentes ye un vector físicu.
Dual de Hodge[editar | editar la fonte]
Nel formalismu de la xeometría diferencial de les variedaes riemannianas la noción de productu vectorial puede amenorgase a una operación de dual de Hodge del productu de dos formes diferenciales naturalmente acomuñaes a dos vectores. Asina'l productu vectorial ye a cencielles:
Onde denotan les 1-formas naturalmente acomuñaes a los dos vectores, y denota l'operador estrella de Hodge.
Xeneralización a n dimensiones[editar | editar la fonte]
Anque'l productu vectorial ta definíu solamente en tres dimensiones, ésti puede xeneralizase a dimensiones, con y namái va tener sentíu si úsense vectores, dependiendo de la dimensión na que se tea. Asina, por casu, en dos dimensiones el productu vectorial xeneralizáu namái tien sentíu si úsase un vector, y la resultancia ye un vector ortogonal.
Dende un puntu de vista tensorial el productu xeneralizáu de n vectores va venir dau por:
Otros productos vectoriales[editar | editar la fonte]
Daos dos vectores, defínense trés operaciones matemátiques de tipu productu ente ellos:
- Productu escalar (la resultancia de la operación ye un escalar)
- Productu vectorial (la resultancia ye un vector)
- Productu tensorial
El productu escalar de vectores dexa determinar ángulos y distancies (vease operador norma) d'una forma fácil y direuto. El productu vectorial apurre una manera pa determinar ángulos y árees de paralelogramos definíos por dos vectores d'una forma tal que va dexar espresar volumes fácilmente por aciu el llamáu productu mistu de tres vectores.
Nel espaciu allegáu bidimensional, , el productu vectorial ye una operación esterna, yá que da como resultáu un vector que nun pertenez al mesmu espaciu vectorial, esto ye al planu definíu polos dos vectores que s'operen, por ser un vector perpendicular a dichu planu. Nel espaciu allegáu tridimensional, , el productu vectorial ye una operación interna.
Ver tamién[editar | editar la fonte]
- Base (álxebra)
- Base ortogonal
- Base ortonormal
- Combinación llinial
- Doble productu vectorial
- Espaciu vectorial
- Independencia llinial
- Productu escalar
- Productu mistu
- Productu tensorial
- Sistema xenerador
Notes y referencies[editar | editar la fonte]
Bibliografía[editar | editar la fonte]
- Ortega, Manuel R. (1989-2006). leición de física (4 volumes) (en castellanu). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7.
- Resnick, Robert & Krane, Kenneth S. (2001). Physics (n'inglés). Nueva York: John Wiley & Sons. ISBN 0-471-32057-9.
- Spiegel, M. & Abellanas, L. (1988). Fórmules y tables de matemática aplicada (en castellanu). McGraw-Hill. ISBN 84-7615-197-7.
Enllaces esternos[editar | editar la fonte]
- Plantía:IMMP
- Weisstein, Eric W. «Cross Product» (inglés). MathWorld. Wolfram Research.




























































