Teorema de Pitágores

Teorema de Pitágores
	teorema

El teorema de Pitágores establez que nun triángulu rectángulu la suma de los cuadraos de los catetos ye igual al cuadráu de la hipotenusa:

a^{2}+b^{2}=c^{2}\,

Demostraciones

Conócense cientos de demostraciones del teorema de Pitágores.

Por distintos allugamientos de triángulos nun mesmu cuadráu

Allugamientu de cuatro triángulos nel interior d'un cuadráu de llau $a+b$

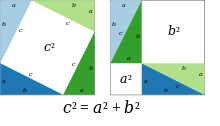
Seya un cuadráu de llau $c$ . Ye posible axuntar cuatro copies del triángulu rectángulu de catetos $a$ y $b$ ya hipotenusa $c$ al rodiu del cuadráu, formando un cuadráu nuevu de llau $a+b$ . L'area d'esti cuadráu grande, poro, ye igual a $c^{2}$ más la suma de les árees de los cuatro triángulos.

Per otru llau, el cuadráu de llau $a+b$ pue formase tamién a partir de los cuatro triángulos rectángulos d'enantes y dos cuadraos de llaos $a$ y $b$ respeutivamente. L'área d'esti cuadráu ye agora $a^{2}+b^{2}$ más les árees de los cuatro triángulos.

En comparando les dos espresiones y desaniciando les árees de los triángulos, s'atopa que $c^{2}=a^{2}+b^{2}$ .

Xeneralizaciones

Teorema del cosenu

El teorema del cosenu ye una xeneralización del teorema de Pitágores pa triángulos arbitrarios. Si'l triángulu tien por llaos $a$ , $b$ y $c$ , esti teorema diz que

c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma

onde $\gamma$ ye l'ángulu ente los llaos $a$ y $b$ . Nos triángulos rectángulos, $\gamma$ ye un ángulu reutu y'l so cosenu ye igual a cero; poro, nesti casu'l teorema del cosenu diz lo mesmu que'l teorema de Pitágores. Amás, si los llaos del triángulu satisfaen la ecuación

c^{2}=a^{2}+b^{2}

entós tien de cumplirse que $2ab\cdot \cos \gamma =0$ , y asina $\gamma$ tien de ser reutu; y'l triángulu orixinal, rectángulu.

Referencies

Enllaces esternos

Wikimedia Commons tien conteníu multimedia tocante a Teorema de Pitágores.