Productos notables

Llámase productos notables a ciertos producto que cumplen regles fixes y que'l so resultáu pue ser escritu por simple inspeición, esto ye, ensin verificar la multiplicación.

Cada productu notable correspuende a una fórmula de factorización. Por casu, la factorización d'una diferencia de cuadraos perfectos ye un productu de dos binomios conxugaos, y recíprocamente.

Factor común

Visualización de la regla de factor común. Forma un nomon.

La resultancia de multiplicar un binomiu $a+b$ por un términu $c$ llógrase aplicando la propiedá distributiva:

$c\cdot (a+b)=c\cdot a+c\cdot b\,$

Na figura axunta reparar que l'área del rectángulu ye $c(a+b)\,$, esto ye, el productu de la base $a+b\,$ pol altor $c\,$, tamién puede llograse como la suma de los dos árees coloriaes: $ca\,$ y $cb\,$

Cuadráu d'un binomiu

Ilustración gráfica del binomiu al cuadráu.

P'alzar un binomiu al cuadráu (esto ye, multiplicalo por sigo mesmu), sumir los cuadraos de cada términu más el doble del productu d'ellos, dando:

$(a+b)^{2}=a^{2}+2ab+b^{2}\,$

Demostración

$(a+b)^{2}=(a+b)\cdot (a+b)=(a+b)\cdot a+(a+b)\cdot b$ $=a\cdot a+b\cdot a+a\cdot b+b\cdot b$ $=a^{2}+2\cdot a\cdot b+b^{2}$

La espresión siguiente: $a^{2}+2ab+b^{2}\;$ conozse como trinomiu cuadráu perfectu.

Cuando'l segundu términu ye negativu, la igualdá que se llogra ye:

$(a-b)^{2}=a^{2}-2ab+b^{2}\,$

Demostración

$(a-b)^{2}=(a+(-b))^{2}$ $=a^{2}+2\cdot a\cdot (-b)+(-b)^{2}$ $=a^{2}-2\cdot a\cdot b+b^{2}$ Fórmula non recomendable cuando nun s'omite'l casu $b=-7$ en $(x-7)^{2}$ induciendo n'abondosos errores. El casu $(-a+b)^{2}=((-a)+b)^{2}$ $=a^{2}-2\cdot a\cdot b+b^{2}$. Finalmente $(-a-b)^{2}=(-(a+b))^{2}=(a+b)^{2}$.

Exemplu:

$(2x-3y)^{2}=(2x)^{2}-2(2x)(3y)+(3y)^{2}\,$

Simplificando:

$(2x-3y)^{2}=4x^{2}-12xy+9y^{2}\,$

Productu de binomios con términu común

Dos binomios con un términu común

Ilustración gráfica del productu de binomios con un términu común.

Pa efectuar un productu de dos binomios con términu común tiense qu'identificar el términu común, nesti casu x, depués aplícase la fórmula siguiente:

$(x+a)(x+b)=x^{2}+(a+b)x+ab\,$

Demostración

$(x+a)\cdot (x+b)=(x+a)x+(x+a)b=(x\cdot x+a\cdot x)+(x\cdot b+a\cdot b)=$ $x\cdot x+a\cdot x+x\cdot b+a\cdot b=$ $x^{2}+(a+b)x+a\cdot b$

Exemplu:

$(x+4)(x-7)=x^{2}-3x-28\,$

$(2y-1)(2y-3)=(2y)^{2}+(-1-3)(2y)+((-1)(-3))=4y^{2}-8y+3$

Tres binomio con términu común

Fórmula xeneral:

$(x+a)(x+b)(x+c)=x^{3}+(a+b+c)x^{2}+(ab+ca+cb)x+abc$

Binomios con un términu común

Fórmula xeneral:

$(x+a_{1})\cdot ...\cdot (x+a_{n})=$ $x^{n}+(a_{1}+...+a_{n})x^{n-1}+$ $((a_{1}a_{2}+a_{1}a_{3}+...+a_{1}a_{n})+$ $(a_{2}a_{3}+...+a_{2}a_{n})+$ $...+$ $(a_{n-1}a_{n}))x^{n-2}+$ $...+$ $(a_{1}\cdot ...\cdot a_{n}).$

Productu de dos binomios conxugaos

Ver tamién: Conxugáu (matemática)

Productu de binomios conxugaos.

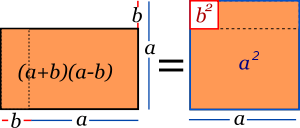
Dos binomios conxugaos estrémense solo nel signu de la operación. Pa la so multiplicación basta alzar los monomios al cuadráu y restalos (obviamente, un términu caltién el signu negativu), colo cual llógrase una diferencia de cuadraos.

$(a+b)(a-b)=a^{2}-b^{2}\,$

Exemplu:

$(3x+5y)(3x-5y)=\,$

$(3x)(3x)+(3x)(-5y)+(5y)(3x)+(5y)(-5y)\,$

Arrexuntando términos:

$(3x+5y)(3x-5y)=9x^{2}-25y^{2}\,$

A esti productu notable tamién se-y conoz como suma pola diferencia.

• Nel casu $(p-a+b+c)(p-a-b-c)=(p-a)^{2}-(b+c)^{2}$, apaecen polinomios.

Cuadráu d'un polinomiu

Elevación d'un trinomiu al cuadráu de forma gráfica.

P'alzar un polinomiu de cualquier cantidá de términos suman los cuadraos de cada términu individual y depués añader el doble de la suma de los productos de cada posible par de términos.

$(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+ac+bc)\,$

$(a+b+c+d)^{2}=a^{2}+b^{2}+c^{2}+d^{2}+2(ab+ac+ad+bc+bd+cd)\,$

Exemplu:

$(3x+2y-5z)^{2}=(3x+2y-5z)(3x+2y-5z)\,$

Multiplicando los monomios:

$(3x+2y-5z)^{2}=3x\cdot 3x+3x\cdot 2y+3x\cdot (-5z)\,$

$+2y\cdot 3x+2y\cdot 2y+2y\cdot (-5z)\,$

$+(-5z)\cdot 3x+(-5z)\cdot 2y+(-5z)\cdot (-5z)\,$

Arrexuntando términos:

$(3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+2(6xy-15xz-10yz)\,$

Depués:

$(3x+2y-5z)^{2}=9x^{2}+4y^{2}+25z^{2}+12xy-30xz-20yz\,$

Romper moldes

$x(x+1)(x+2)(x+3)+1=(x^{2}+3x+1)^{2}$.

Cubu d'un binomiu

Descomposición volumétrica del binomiu al cubu.

Pa calcular el cubu d'un binomiu sumir, socesivamente:

• El cubu del primer términu.
• El triple productu del cuadráu del primeru pel segundu.
• El triple productu del primeru pol cuadráu del segundu.
• El cubu del segundu términu.

$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}\,$

Identidaes de Cauchy:

$(a+b)^{3}=a^{3}+b^{3}+3ab(a+b)\,$

Exemplu:

$(x+2y)^{3}=x^{3}+3(x)^{2}(2y)+3(x)(2y)^{2}+(2y)^{3}\,$

Arrexuntando términos:

$(x+2y)^{3}=x^{3}+6x^{2}y+6xy^{2}+8y^{3}\,$

Si la operación del binomiu implica resta, la resultancia ye:

• El cubu del primer términu.
• Menos el triple productu del cuadráu del primeru pel segundu.
• Más el triple productu del primeru pol cuadráu del segundu.
• Menos el cubu del segundu términu.

$(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}\,$

Identidaes de Cauchy:

$(a-b)^{3}=a^{3}-b^{3}-3ab(a-b)\,$

Exemplu:

$(x-2y)^{3}=x^{3}-3(x)^{2}(2y)+3(x)(2y)^{2}-(2y)^{3}\,$

Arrexuntando términos:

$(x-2y)^{3}=x^{3}-6x^{2}y+6xy^{2}-8y^{3}\,$

Identidá de Argand

$(x^{2}+x+1)(x^{2}-x+1)=x^{4}+x^{2}+1\,$

Identidaes de Gauss

$a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ac)\,$

$a^{3}+b^{3}+c^{3}-3abc={\frac {1}{2}}(a+b+c)[(a-b)^{2}+(b-c)^{2}+(a-c)^{2}]\,$

Identidaes de Legendre

$(a+b)^{2}+(a-b)^{2}=2(a^{2}+b^{2})\,$

$(a+b)^{2}-(a-b)^{2}=4ab\,$

$(a+b)^{4}-(a-b)^{4}=8ab(a^{2}+b^{2})\,$

Identidaes de Lagrange

Artículu principal: Identidá de Lagrange

$(a^{2}+b^{2})(x^{2}+y^{2})=(ax+by)^{2}+(ai-bx)^{2}\,$

$(a^{2}+b^{2}+c^{2})(x^{2}+y^{2}+z^{2})=(ax+by+cz)^{2}+(ai-bx)^{2}+(az-cx)^{2}+(bz-cy)^{2}\,$

Otres identidaes

Yá que la notabilidad d'un productu ye un conceutu ambiguu, nun esiste una llista determinante qu'indique a cuál productos puédese-yos considerar notables, y a cuálos non. A otres fórmules, anque menos usaes que les anteriores, en ciertos contestos puede calificáse-yos de productos notables. Ente elles destáquense:

Adición de cubos:

$a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})\,$

Diferencia de cubos:

$a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})\,$

Ye más frecuente listar los dos espresiones anteriores como les fórmules de factorización, una y bones los productos nun tienen una forma particularmente simétrica, pero la resultancia sí (oldéese, por casu, cola fórmula de binomiu al cubu).

$(a+b)(a^{2}-ab+b^{2})=a^{3}+b^{3}\,$

$(a-b)(a^{2}+ab+b^{2})=a^{3}-b^{3}\,$

La suma y la diferencia de cubos pueden xeneralizase a sumes y diferencies de potencies enésimes (o n - ésimas: xⁿ).

Suma de dos cuadraos

$a^{2}+b^{2}=(a+bi)(a-bi)\,$

Ónde i ye la unidá imaxinaria (√-1)

Demostración

$(a+bi)(a-bi)=a^{2}-(bi)^{2}=a^{2}-(b^{2}\cdot i^{2})=a^{2}-(b^{2}(-1))=a^{2}-(-b^{2})=a^{2}+b^{2}$

Suma de potencies enésimes:

Si –namái si– n ye impar, $a^{n}+b^{n}=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^{2}-\cdots +b^{n-1})\,$

Diferencia de potencies enésimes:

$a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+\cdots +b^{n-1})\,$

Les fórmules de binomiu al cuadráu y binomiu al cubu pueden xeneralizase por aciu el teorema del binomiu.

Pa representar el cubu d'un monomiu, como estrema de dos cuadraos, esiste una fórmula atélite:

$a^{3}=\left({\frac {(a+1)a}{2}}\right)^{2}-\left({\frac {(a-1)a}{2}}\right)^{2}$

Ver tamién

• Binomiu
• Trinomiu
• Factorización
• Triángulu de Pascal
• Cocientes notables
• Completar el cuadráu

Bibliografía

• • Barreto García, Julio César. «Los gnómones y la solución geométrica de ecuaciones de segundo grado y su aplicación a los productos notables». Revista Suma.
  • Barreto García, Julio César. (2014). «Productos Notables en el Espacio: Deducciones con diversas Actividades y Aplicaciones».Coleición de Secundaria. Volumen 3. ISBN-10: 1503072045 ISBN-13: 978-1503072046. Editorial Amazon.
  • Barreto García, Julio César.(2014). «Polinomios Algebraicos y Geométricos (Productos Notables Planos y Factorización)».Coleición de Secundaria. Volumen 2. ISBN-10: 1502888963 ISBN-13: 978-1502888969. Editorial Amazon.
  • Barreto García, Julio César. (2014). «Didáctica de la geometría espacial». ISBN-10: 3659055875 ISBN-13: 978-3659055874. Editorial EAE.
  • Barreto García, Julio César. (2012). «Aplicación de la didáctica de la geometría en secundaria: Didáctica de la Geometría». ISBN-10: 3659055875 ISBN-13: 978-3659055874. Editorial EAE.
  • Barreto García, Julio César. «Dinamización Matemática: Deducción geométrica de los productos notables en el espacio tridimensional como recurso didáctico en el proceso de enseñanza aprendizaje de la matemática». Revista Unión.
  • Barreto García, Julio César. «Dos perspectivas geométricas de la diferencia de cuadrados como recurso didáctico en el proceso de enseñanza-aprendizaje de la matemática». Revista Matematicalia.
  • Barreto García, Julio César. «Perceición geométrica de los productos notables y de la media geométrica». Revista Números.
  • Wentworth, George Albert; Smith, David Eugene (1980). Elemento d'álxebra, 2ª, Boston: Porrúa, páx. 458. ISBN 9789684325296.
    

• Datos: Q1971429