Fuercia centrípeta
| Fuercia centrípeta | |
|---|---|
| fuercia | |
 | |
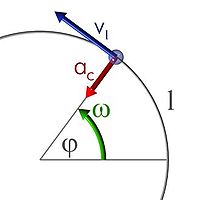
Llámase "fuercia centrípeta" a encomalo o al componente de la fuercia qu'actúa sobre un oxetu en movimientu sobre una trayeutoria curvillinia y que ta dirixida escontra'l centru de combadura de la trayeutoria.
El términu centrípeta» provién de les pallabres llatines centrum, «centru» y petere, «dirixise escontra», y puede ser llograda a partir de les lleis de Newton. Nel casu d'un oxetu que se mueve en trayeutoria circular con velocidá cambiante, la fuercia neto sobre'l cuerpu puede ser descompuesta nun componente perpendicular que camuda la direición del movimientu y unu tanxencial, paralelu a la velocidá, que modifica'l módulu de la velocidá.
La fuercia centrípeta nun tien de ser confundida cola fuercia centrífuga, tal como s'esplica na seición Tracamundios comunes.
Fuercia centrípeta en mecánica newtoniana[editar | editar la fonte]
Los oxetos con movimientu rectilliniu uniforme tienen una velocidá constante; pero un oxetu que se mueva sobre una trayeutoria circular con rapidez constante esperimenta de cutio un cambéu na direición del so movimientu, esto ye, na direición de la velocidá. Puesto que la velocidá camuda, esiste una aceleración. La magnitú d'esti cambéu de direición de la velocidá por unidá de tiempu ye l'aceleración centrípeta, representada por un vector empobináu escontra'l centru de la circunferencia dau por ecuación|||left}} Onde:
- ye l'aceleración centrípeta.
- ye'l módulu de la velocidá.
- ye'l radiu de la trayeutoria circular (polo xeneral, el radiu de combadura).
- el vector de posición.
- el versor radial.
- la velocidá angular.
Según la segunda llei de Newton, por que se produza una aceleración tien d'actuar una fuercia na direición d'esa aceleración. Asina, si consideramos una partícula de masa en movimientu circular uniforme, va tar sometida a una fuercia centrípeta dada por:
Exemplu[editar | editar la fonte]
Supongamos qu'arreyamos una pelota con una cuerda y facer xirar en círculu a velocidá angular constante. La pelota mover nuna trayeutoria circular porque la cuerda exerz sobre ella una fuercia centrípeta.
Otru exemplu puede vese en Modelu de Tiovivo, onde un programa realizáu en llinguaxe Java dexa parametrizar dalgunes de les variables qu'intervienen utilizando un carrusel.
Tracamundios comunes[editar | editar la fonte]
En dellos testos docentes introductorios ye frecuente atopar ciertu tracamundiu ente los términos "fuercia centrípeta" y "fuercia centrífuga". La fuercia centrífuga ye una fuercia ficticio que "apaez" pa un observador qu'usa un marcu de referencia en rotación pa describir el movimientu. Sicasí, un observador nun marcu de referencia inercial nun percibe nenguna fuercia centrífuga, ente que sí ve una fuercia real llamada fuercia centrípeta que ye la qu'obliga a un móvil a curvar la so trayeutoria na direición de felicidá fuercia. El problema mora en que nun sistema de referencia en rotación la fuercia centrífuga (ficticia) albidrada por un observador en reposu en dichu referencial coincide en magnitud –pero en sentíu contrariu– cola fuercia centrípeta (real) necesaria pa caltener un cuerpu en reposu en tal sistema de referencia en rotación.
Tampoco la fuercia centrípeta tien de confundise cola denomada fuercia central. La fuercia central ye una fuercia real qu'actúa sobre un cuerpu y que cumple con dos condiciones:
- la so magnitú depende namái de la distancia del cuerpu a un puntu que se denomina centru de fuercies y #
la so llinia d'aición pasa pol citáu centru de fuercies. Exemplos de fuercies centrales son la fuercia gravitatoria y la fuercia electrostática. Frecuentemente, la fuercia centrípeta ye una fuercia central. Una esceición asocede cuando'l centru de mases nun coincide col centru xeométricu del oxetu sobre'l cual actúen les fuercies, colo qu'hai que poner especial énfasis sobre la direición de la fuercia centrípeta y los puntos onde actúa. Un exemplu claru d'ésti fenómenu asocede cola dinámica d'un cilindru inhomogéneo que rueda sobre un planu inclináu hasta desapegase del mesmu.[1]
Deducción de l'aceleración centrípeta[editar | editar la fonte]
Demostración xeométrica[editar | editar la fonte]

Puesto que la velocidá ye siempres tanxente a la trayeutoria, el vector siempres ye perpendicular al vector de posición. Como l'estremu del vector muévese describiendo una circunferencia de radiu , l'estremu del vector facer de manera análoga. La circunferencia a la derecha amuesa la forma en que camuda la velocidá col tiempu. Dicha circunferencia representa la hodógrafa del movimientu.
El cambéu de la velocidá nel tiempu ye l'aceleración, y yá que la velocidá camuda de manera similar a como lo fai'l vector de posición, l'aceleración en cada intre tamién ye perpendicular a la velocidá nesi intre, polo que podemos dibuxales como vectores tanxentes a la circunferencia.
Una y bones los vectores de posición y velocidá xiren conxuntamente, el periodu T (tiempu emplegáu nuna vuelta completa) va ser el mesmu en dambos casos.
Pal periodu de la partícula na trayeutoria circular tenemos
y, por analoxía, cola hodógrafa de la derecha tenemos
Igualando dambes ecuaciones, y estenando llogramos.
Comparando la trayeutoria (esquierda) cola so hodógrafa (derecha), deduzse que l'aceleración apunta escontra'l centru de la circunferencia, en forma opuesta al vector . Esto podemos facer tornando cada unu de los vectores a la so posición orixinal nel círculu de la esquierda. Si xunto con ellos llevamos los vectores , podrá notase el fechu de qu'estos postreros efeutivamente apunten escontra'l centru.
Deducción usando'l cálculu[editar | editar la fonte]

Otru métodu pa deducir la ecuación de l'aceleración centrípeta consiste n'espresar la ecuación de la trayeutoria circular n'ecuaciones paramétricas:
onde : ye la velocidá angular
- ye'l tiempu y
derivar dos veces socesives con respectu del tiempu
de cuenta
que
que pon de manifiestu que l'aceleración ta dirixida escontra'l centru de la trayectoría circular y que'l so módulu vien dau por:
Fuercia centrípeta en mecánica relativista[editar | editar la fonte]
En mecánica relativista el cociente ente la fuercia centrípeta y l'aceleración centrípeta, ye distinta del cociente ente la fuercia tanxencial y l'aceleración tanxencial. Esto introduz una diferencia fundamental col casu newtoniano: l'aceleración y la fuercia relativistes nun son vectores necesariamente paralelos:
De la rellación anterior, deduzse que la fuercia y l'aceleración namái son paraleles en dos casos:
El primer casu dase cuando l'aceleración y la velocidá son perpendiculares, cosa qu'asocede por casu el movimientu circular uniforme. El segundu casu dar nun movimientu rectilliniu. En cualesquier otru tipu de movimientu polo xeneral la fuercia y l'aceleración nun van ser permanentemente paraleles.
Ver tamién[editar | editar la fonte]
Referencies[editar | editar la fonte]
- ↑ «A jumping cylinder on an inclined plane». Eur. J. Phys. (IOP) 33 (5): páxs. 1359-1365. 25 de xunetu de 2012. doi:. https://www.researchgate.net/publication/236030807_A_jumping_cylinder_on_an_inclined_plane_A_jumping_cylinder_on_an_inclined_plane. Consultáu'l 25 d'abril de 2016.
Bibliografía[editar | editar la fonte]
- Marion, Jerry B. (1996). Dinámica clásica de les partícules y sistemes (en castellanu). Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
- Resnick, Robert & Krane, Kenneth S. (2001). Physics (n'inglés). New York: John Wiley & Sons.
- Resnick, Robert & Halliday, David (2004). Física 4ª (en castellanu). CECSA, Méxicu. ISBN 970-24-0257-3.

























![{\displaystyle \mathbf {F} ={\frac {d}{dt}}\left({\frac {m\mathbf {v} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\right)={\frac {m\mathbf {v} }{\left[1-{\frac {v^{2}}{c^{2}}}\right]^{3/2}}}\left({\frac {\mathbf {v} }{c^{2}}}\cdot \mathbf {a} \right)+{\frac {m\mathbf {a} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a4906883865776a7bca11426d8de904d1cee2b2)
