Orbital atómicu
| Orbital atómicu | |
|---|---|
| tipu de función matemática | |
|
función matemática y orbital (en) | |
 | |

Denómase orbital, nun átomu, a los estaos estacionarios de la función d'onda d'un electrón (funciones propies del Hamiltonianu (H) na ecuación de Schrödinger HΨ = EΨ; Ψ la función d'onda ). Sicasí, los orbitales nun representen la posición concreta d'un electrón nel espaciu, que nun pue conocese pola mor de la so natura ondulatoria, sinón que llenden una rexón del espaciu na que la probabilidá d'atopar al electrón ye elevada (polo que delles vegaes al orbital se-y anoma Rexón espacio-enerxética de manifestación probabilística electrónica o REEMPE).
Introducción
[editar | editar la fonte]Nel casu del átomu d'hidróxenu, Schrödinger foi pa resolver la ecuación anterior de forma exauta, atopando que les funciones d'onda tán determinaes polos valores de cuatro númberos cuánticos n, l, ml y s.
| Númberu cuánticu | Nome | Valores posibles | Significáu nel orbital |
|---|---|---|---|
| n | Principal | 1,2,3,... | Nivel enerxéticu y midida |
| l | Secundariu o azimutal | 0,... (n-1) | Subnivel enerxéticu y forma |
| ml | Magnéticu | -l,...,0,...,+l | Orientación nel espaciu |
| s | de spin | -1/2 o +1/2 | Comportamientu d'imán del electrón |
- El valor del númberu cuánticu n (númberu cuánticu principal, toma valores 1,2,3...) define'l tamañu del orbital. Cuanto mayor seya, mayor sedrá'l volume. Tamién ye'l que tien mayor influyencia na enerxía del orbital.
- El valor del númberu cuánticu l (númberu cuánticu del momentu angular) indica la forma del orbital y el momentu angular. El momentu angular vien dau por
La notación (procedente de la espectroscopia) ye la que vien darréu:
- Pa l = 0, orbitales s
- Pa l = 1, orbitales p
- Pa l = 2, obitales d
- Pa l = 3, orbitales f
- Pa l = 4, orbitales g; siguiéndose yá l'orde alfabéticu.
- El valor de ml (númberu cuánticu magnéticu) define la orientación espacial del orbital frente a un campu magnéticu esternu. Pa la proyeición del momentu angular frente al campo esternu, verifícase:
- El valor de s (númberu cuánticu d'espín) pue ser +1/2 o -1/2. (Al orbital ensin el valor de s llámase-y orbital espacial, al orbital col valor de s llámase-y espínorbital.)
La función d'onda pue descomponese, emplegando coordenaes esfériques, de la siguiente forma:
- Ψn, l, ml = Rn, l (r) Θl, ml (θ) Φml (φ)
Onde
- Rn, l (r) representa la distancia del electrón al nucleu y
- Θl, ml (θ) Φml (φ) la xeometría del orbital.
Pa la representación del orbital emplegase la función cuadráu, |Θl, ml (θ)|2 |Φml (φ)|2, ya que ésta ye proporcional a la densidá de carga y por tanto a la densidá de probabilidá, ye dicir, el volume qu'enzarra la mayor parte de la probabilidá d'atopar al electrón o, si se prefier, el volume o rexón del espaciu na que l'electrón pasa la mayor parte del tiempu.
Más acullá del átomu d'hidróxenu
[editar | editar la fonte]En sen estrictu, los orbitales son construcciones matemátiques que faen por describir, de forma afitada cola mecánica cuántica, los estaos estacionarios d'un electrón nun campu llétricu central (dao que'l nucleu nun ta descritu de forma esplícita, nin siquieramente se describe de forma completa l'átomu d'hidróxenu). Estes construcciones matemátiques nun tán preparaes, pol so orixe monoelectrónicu, para tener en cuenta nin la correllación ente electrones nin l'antisimetría desixida pola estadística de Fermi (los electrones son fermiones).
Sicasí, saliéndose del so sen estrictu, demostraron ser de gran utilidá pa los químicos, de forma que s'utilicen non solo pa sistemas polielectrónicos, sinón tamién pa sistemes polinucleares, como les molécules. Tamién más acullá del so sen estrictu, los químicos refiérense a ellos como entes físicos más que como construcciones matemátiques, con espresiones como "nun orbital caben dos electrones".
Formes de los orbitales
[editar | editar la fonte]Por simplicidá, recuéyense les formes de la parte angular de los orbitales, escaeciendo los nueyos radiales, que siempre tienen forma esférico.
Orbital s
[editar | editar la fonte]L'orbital s tien simetría esférico alredor del nucleu atómicu. Na figura d'embaxo amuésense dos formes alternatives de representar la ñube electrónica d'un orbital s: na primera, la probabilidá d'atopar al electrón (representada pola densidá de puntos) amenorga según mos alloñamos del centru; na segunda, represéntase'l volume esféricu nel que l'electrón pasa la mayor parte del tiempu. Principalmente pola simplicidá de la representación, ye ésta segunda forma la que s'emplega davezu. Pa valores del númberu cuánticu principal mayores qu'ún, la función densidá electrónica presenta n-1 nueyos nos que la probabilidá tiende a cero; nestos casos la probabilidá d'atopar al electrón concéntrase a della distancia del nucleu.

Orbital p
[editar | editar la fonte]La forma xeométrica de los orbitales p ye la de dos esferes achataes haza'l puntu de contautu (el nucleu atómicu) y orientaes según les exes de coordenaes. En función de los valores que pue tomar el tercer númberu cuánticu ml (-1, 0 y 1), obtiénense los tres orbitales p simétricos respeuto a les exes x, z ya y. De la mesma forma que'l casu d'enantes, los orbitales p presenten n-2 nueyos radiales na densidá electrónica, de mou qu'al incrementarse'l valor del númberu cuánticu principal la probabilidá d'atopar l'electrón allóñase del nucleu atómicu.

Orbital d
[editar | editar la fonte]Los orbitales d tienen una forma más diversa: cuatro d'ellos tienen forma de 4 llóbulos de signos alternaos (dos planos nodales, n'estremaes orientaciones del espaciu), y el postreru ye un doble llóbulu arrodiáu per un aniellu (un doble conu nodal). Siguiendo la mesma tendencia, presenten n-3 nueyos radiales.

Orbital f
[editar | editar la fonte]Los orbitales f tienen formes inda más esótiques, que se puen derivar d'añader un planu nodal a les formes de los orbitales d. Presenten n-4 nueyos radiales.
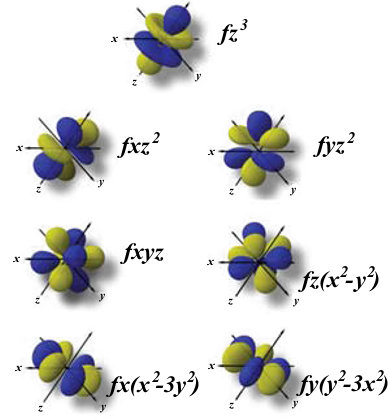
Nota: Imáxenes xeneraes col programa Orbital Viewer, (C) David Manthey
Ver tamién
[editar | editar la fonte]Referencies
[editar | editar la fonte]Enllaces esternos
[editar | editar la fonte]
 Wikimedia Commons tien conteníu multimedia tocante a Orbital atómicu.
Wikimedia Commons tien conteníu multimedia tocante a Orbital atómicu.


