Fuercia de Lorentz
| Fuercia de Lorentz | |
|---|---|
| fuercia | |
 | |

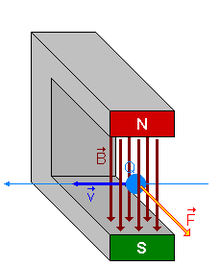
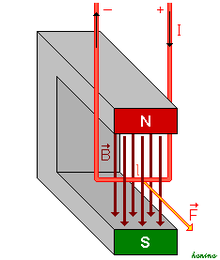
En física, la fuercia de Lorentz ye la fuercia exercida pol campu electromagnéticu que recibe una partícula cargada o una corriente llétrica.
Forma clásica[editar | editar la fonte]
Pa una partícula sometida a un campu llétrico combináu con un campu magnéticu, la fuercia electromagnético total o fuercia de Lorentz sobre esa partícula vien dada por:
onde ye la velocidá de la carga, ye'l vector intensidá de campu llétrico y ye'l vector inducción magnética. La espresión siguiente ta rellacionada cola fuercia de Laplace o fuercia sobre un filo conductor pol que circula corriente:
onde ye'l llargor del conductor, ye la intensidá de corriente y la inducción magnética. A pesar de ser una consecuencia direuta d'ella, esta última espresión históricamente atopóse primero que l'anterior, por cuenta de que les corrientes llétriques remanábense primero que tuviera claru si la carga llétrica yera un fluyíu continuu o taba constituyida por pequeñes cargues discretes.
Formes alternatives[editar | editar la fonte]
Forma integral[editar | editar la fonte]
Si los campos llétricu y magnéticu nun son modificaos pola presencia de la densidá de carga llétrica ρ y la densidá de corriente , y los dos últimes nun son modificar por dichos campos, la fuercia de Lorentz puede espresase como:
Como polo xeneral esto nun ye ciertu, el resolución de les fuercies resultantes rique l'usu de considerancies enerxétiques y el resolución d'ecuaciones diferenciales derivaes de les ecuaciones de Maxwell.
Forma tensorial[editar | editar la fonte]
En teoría de la relatividá convien escribir les lleis físiques en forma explícitamente tensorial. Eso implica que les magnitúes que se tresformen vectorialmente como, por casu, la velocidá o la densidá de corriente, tienen de ser representaes por cuadrivectores. La fuercia de Lorentz escrita en forma explícitamente tensorial ye:
(espresión tensorial relativista)
Onde:
- son les componentes del cuadrivector fuercia.
- son les componentes del cuadrivelocidad, siendo el factor de Lorentz.
- son les componentes del tensor de campu electromagnéticu que les sos componentes rellacionar cola parte llétrica y magnética del campu asina:
Fuercia de Lorentz y tercer llei de Newton[editar | editar la fonte]
La fuercia magnético que s'exercen dos partícules en movimientu nun satisfai'l principiu d'aición-reaición o tercer llei de Newton, esto ye, la fuercia exercida pola primer partícula sobre la segunda nun ye igual a encomalo exercida pola segunda partícula sobre la primera.[1] Esto puédese comprobar por cálculu direutu considerando dos cargues puntuales. La fuercia de la partícula 1 sobre la partícula 2 ye, utilizando la Llei de Biot-Savart:
Onde los son los valores de posición respeutivos, les velocidaes lliniales respeutives, qi les cargues respeutives, d la distancia ente los dos partícules y los campos magnéticos. Análogamente la fuercia de la partícula 2 sobre la partícula 1 ye:
Emplegando la identidá puede trate que la primer fuercia ta nel planu formáu por y que la segunda fuercia ta nel planu formáu por y .
Ver tamién[editar | editar la fonte]
Referencies[editar | editar la fonte]
- ↑ J. R. Taylor, 2005, cap. 1.
Bibliografía[editar | editar la fonte]
- Taylor, John Robert (2005). Classical mechanics (n'inglés). University Science Books.
Enllaces esternos[editar | editar la fonte]
Animaciones y simulaciones[editar | editar la fonte]
- Fuercia de Lorentz (en)
























