Teorema de la bola peluda

Si un campu vectorial sobre una esfera simbolizar por pelos de llargor constante, el teorema de la bola peluda axusta que la esfera contién siquier un rizu. La figura contién dos, unu en cada polu.

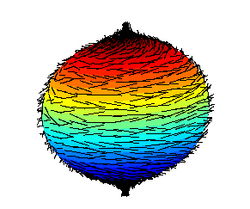
En matemática, y más precisamente en topoloxía diferencial, el teorema de la bola peluda ye un resultáu que s'aplica a esferes qu'en cada puntu tienen un vector, visualizáu como un pelo» tanxente a la superficie. Afirma que la función qu'acomuña a cada puntu de la esfera'l vector almite siquier un puntu de discontinuidá, lo que significa que'l peñáu contién un «bucle» o «rizu», ye dicir que va haber zones vacíes (o calvez).

De manera más rigorosa, un campu vectorial continuu definíu sobre una esfera de dimensión par, siquier igual a 2, anular en siquier un puntu. Esta resultancia rellacionar colos llamaos teoremas de puntu fixu y tien numberoses aplicaciones n'árees como la meteoroloxía o la computación gráfica.

Representación intuitiva

Represéntase intuitivamente una esfera recubierta per pelos llisos y non crespos, cada puntu de la esfera ye'l raigañu d'un pelo. De siguío, considérase la proyeición sobre'l planu tanxente a la esfera nel puntu en que'l pelo crez: el conxuntu d'estes proyeiciones da una bona idea d'un campu de vectores tangente a la esfera. Lo que se busca entós ye "peñar" estos pelos alisar sobre la superficie de la bola, evitando les discontinuidaes: el peñáu nun tien raya, nun se dexa a nengún pelo camudar sópito de direición con al respective de los otros. El teorema afirma entós que ye imposible llograr esta resultancia: cualquier intentu va causar siquier un rizu, ye dicir un puntu en qu'un pelo va parase.

Enunciáu

Teorema de la bola peluda Si $n\$ ye un enteru par siquier igual a $2\$, tou campu vectorial continuu $X\$ sobre la esfera real $S_{n}\$ anular nun puntu siquier; ye dicir qu'esiste $v\$ (que depende de $X\$) tal que: $X(v)=0\$.

Nota: en dimensión impar, sí ye posible construyir campos vectoriales continuos que nun s'anulen nunca.

Historia

Esti teorema foi demostráu per primer vegada por Luitzen Egbertus Jan Brouwer en 1912. La prueba xeneraliza los resultaos llograes con anterioridá como'l teorema de la curva de Jordan o los trabayos de Leopold Kronecker sobre les funciones de cutio diferenciables de la esfera real de dimensión n- 1 nun espaciu vectorial de dimensión n. Estes resultancies, anque de formulación intuitiva, riquen pa la so demostración desarrollos dacuando téunicos. Un exemplu arquetípico de resultancies de la mesma naturaleza ye'l teorema del puntu fixu de Brouwer, que enuncia que toa aplicación continua d'una bola zarrada d'un espaciu vectorial euclidianu de dimensión finita nél mesmu, almite un puntu fixu.

Demostración

Munches de les demostraciones d'esti teorema son por «amenorgamientu al absurdu». Los formalismos matemáticos riquíos en delles d'elles escapen a les pretensiones del presente artículu.^{[Ver bibliografía]}

Demostración visual pol discu

Ye una demostración qu'utiliza l'argumentu del reductio ad absurdum (pueden construyise análogos tridimensionales: quier demostrase que nun puede haber campu vectorial tanxente y continuu, que nun s'anule nunca sobre la esfera ordinaria nel espaciu tridimensional). Al razonar pol absurdu, supónse que sí esiste una aplicación continua $f\$ del discu unitariu nél mesmu, tal que $f(x)\$ ye distinta de $x\$ pa cualesquier $x\$ del discu. Lo que se busca ye fabricar una bola peluda ensin rizu nin calvez, y llograr asina una contradicción.

Si tiense una aplicación $f\$ ensin puntu fixu, entós cada puntu $x\$ del discu dexa definir un vector non nulu, el vector $f(x)-x\$. Intuitivamente, la idea ye «plegar» una esfera cortada pola metá, y faela coincidir esautamente col semi-discu.

• 
• 
• 
• 
• 
• 

Al pegar nuevamente dambos hemisferios de la esfera, los campos tanxentes recompónense de cutio, llográndose asina un «peñáu» continuu y ensin «calvez», que ye la contradicción deseyada.

Formalización xeométrica

Razónase nuevamente pol absurdu. Dada una esfera, escuéyense un polu norte y un polu sur, según una orientación. D'esta miente puede falase de paralelos de la esfera y empobinalos de manera continua. Adicionalmente, defínese un sistema referencial móvil tanxente a la esfera. Puede acomuñáse-y entós a cada paralelu un númberu: el númberu de vueltes del campu vectorial nel sistema móvil a lo llargo d'esi paralelu. Esti númberu ta bien definíu pos el campu vectorial nun s'anula; depende de cutio de la llatitú del paralelu -según los resultaos estándares sobre la continuidá del númberu de vueltes- y ye enteru. Polo tanto ye constante.

De siguío, calcúlase'l númberu de vueltes na vecindá del polu norte, puntu en que'l sistema de referencia móvil cesa de tar definíu. Pa desaniciar esta dificultá, proyéctense al empar el campu vectorial $v\$ y ye sistema móvil sobre'l planu tanxente al polu norte. La orientación d'esti planu tanxente deducir de la orientación de la esfera. Por continuidá, el númberu de vueltes nun camuda y vale $m\$ y $m\$ vale $+1\$ o $-1\$ según la eleición de la orientación de los paralelos.

Siguiendo un razonamientu similar nuna vecindá del polu sur, el sistema móvil va dar una vuelta alredor del polu sur nel sentíu de los paralelos, mas pa caltener una orientación coherente cola de la esfera, en cuantes que planu nel espaciu de tres dimensiones, el planu tanxente tien de tar empobináu nel sentíu opuestu, y polo tanto'l númberu de vueltes va ser $-m\$, lo cual ye una contradicción.

Formalización analítica

Pal desenvolvimientu alxebraicu formal de les demostraciones espuestes, puede tomase, por casu, $x\$ como un puntu corriente de la esfera y $v(x)\$ el campu de vectores; de siguío se parametriza la esfera en coordenaes polares (suponiendo un radiu 1):

$x_{1}=\cos \theta \cos \phi ,\quad x_{2}=\sin \theta \cos \phi ,\quad x_{3}=\sin \phi$

con 0≤$\theta$<2$\pi$ y $-\pi /2$≤ $\phi$≤$\pi /2$. La resultancia amuesa la contradicción afilvanada, al calcular el númberu de vueltes del campu tanxente, con una determinada orientación, na vecindá de los polos.

Demostración de Milnor

Sía $X\$ un campu vectorial conteníu en $S_{n}\$ y a valores nel espaciu euclídeo $V\$ de dimensión $n+1\$, con $n\$ par. Demostrar pol absurdu qu'esta funcíón tien d'anulase por fuerza en siquier un puntu $v\$ de la esfera. Nótase $|v|\$ la norma euclidiana d'un vector $v\$ de $X\$, y $(v|w)\$ el productu esguilar euclidianu de $v\$ y $w\$, pertenecientes a $X\$.

Xeneralización

Nun toru la situación ye distinta.

La demostración analítica debida a Milnor xeneraliza'l teorema al casu de cualquier dimensión. Una demostración llixeramente distinta ye debida a A. Rogers.

Otres pruebes basar en conceutos de la topoloxía alxebraica; una demostración clásica utiliza la carauterística de Euler; tamién puede formulase como un casu particular del teorema de Poincaré-Hopf; otres pruebes basar en propiedaes d'homotopía matemática (teorema de Borsuk-Ulam). Nel casu de la esfera ordinaria, ye posible deducir una demostración a partir del lema de Sperner.

Esiste un argumentu rellacionáu (en topoloxía alxebraica) que se basa nel númberu de Lefschetz y los númberos de Betti: nuna 2-esfera, el númberu de componentes coneutaes (númberu de Betti) son 1, 0, 1, 0, 0, ... Los númberos de Lefschetz (trazar total d'homoloxía) de la función identidá ye igual a 2; al integrar el campu vectorial, llógrase un difeomorfismo de la esfera. Ríquese daqué más de trabayu rigorosu p'amosar que, por cuenta de que'l númberu de Lefschetz nun s'anula, tien d'haber un puntu nel que'l campu vectorial sía cero.

La xeneralización del teorema ta íntimamente coneutada cola carauterística de Euler χ: la 2n-esfera nun tien un campu vectorial que nun s'anule pa n ≥ 1. Esto ye una consecuencia direuta del teorema de Poincaré–Hopf. Nel casu específicu d'un toru matemáticu, por casu, la carauterística de Euler ye 0, polo que sí ye posible llograr un peñáu ensin bucles nin zones clares.

Aplicaciones y consecuencies

Les consecuencies del teorema son numberoses y nun se llinden a les matemátiques.

Teorema del puntu fixu de Brouwer

Ye posible demostrar el teorema del puntu fixu de Brouwer a partir del teorema de la bola peluda:

Sía $n\$ un enteru siquier igual a $1\$ y $B_{n}\$ la bola zarrada centrada nel orixe de radiu $1\$ nel espaciu euclídeo $V\$ de $n\$ dimensiones. Sía $f\$ una aplicación continua de $B_{n}\$ nella mesma. Entós $f\$ tien un puntu fixu; n'otres pallabres, esiste $x\$ en $B_{n}\$ tal que $f(x)=x\$.

Corolariu

Una consecuencia del teorema de la bola peluda ye que toa función continua que «mapee» una esfera en sí mesma tien o bien un puntu fixu o bien un puntu que se mapea nel so puntu antípodo. Esto puédese ver al tresformar una función nun campu vectorial tanxente y definiendo por casu una proyeición estereográfica de la función sobre la esfera. El teorema asegura qua va haber siquier un puntu p pal cual la proyeición va ser 0.

Meteoroloxía

Güeyu del ciclón tropical.

El teorema tien consecuencies en meteoroloxía; considérase una modelización esquemática del vientu como vector definíu de cutio en cada puntu sobre la superficie del planeta con atmósfera. Como una idealización, el vientu tien componentes vectoriales bidimensionales, y el so movimientu a lo llargo de la exa vertical ye nulu.

So estes condiciones, la falta absoluta de vientu correspuende a una solución posible: el campu de vectores nulos. Esti escenariu nun presenta mayor interés dende'l puntu de vista del teorema, y ye físicamente irrealista (vientu siempres va haber). Nel casu en qu'hai daqué de vientu, el teorema de la bola peluda diz qu'en tou momentu tien d'haber siquier un puntu nel planeta ensin nada de vientu.

Nun sentíu físicu, esta zona de non vientu correspuende al güeyu d'un ciclón o anticiclón (efeutu observable, por casu, na vellosidá d'una pelota de tenis, de forma espiral alredor d'esta zona). El teorema de la bola peluda impon la esistencia permanente d'un puntu sobre la tierra onde'l vientu se modeliza por un sistema arremolináu y, nel so centru, un güeyu.

Esta consecuencia reparar de fechu na realidá. El teorema nun diz nada sicasí alrodiu de la talla del vórtice o la potencia de los vientos que lu arrodien.

Computación gráfica

Campu vectorial continuu tanxente sobre una 2-esfera.

Un problema común en computación gráfica ye'l de xenerar, nel espaciu tridimensional, un vector non nulu que sía ortogonal a una zona non nula dada. Nun esiste una función continua que pueda faer esto pa tolos vectores non nulos dados. Este ye un corolariu del teorema de la bola peluda. Pa velo, puede considerase'l vector dau como'l radiu d'una esfera: atopar un vector ortogonal non nulu ortogonal a unu dadu sería equivalente a atopar un vector non nulu que sía tanxente a la superficie d'esa esfera. El teorema asegura que nun esiste una función continua que pueda definise en cada puntu d'una esfera (i.e. pa cada vector dau).

Ver tamién

• Teorema del puntu fixu de Brouwer
• Teoremas de puntu fixu

Bibliografía

• J. W. Milnor, Topology from the differentiable viewpoint Princeton Univ. 1997 ISBN 069104833957. (n'inglés)
• N. Y. Chinn W. G. Steenrod Topologie élémentaire Dunod 1991 ISBN 2040048480. (en francés)
• M. Eisenberg, R. Guy, A Proof of the Hairy Ball Theorem The American Mathematical Monthly Vol. 86, Non. 7 (Aug. — Sep., 1979), pp. 571–574. (n'inglés)
• Murray Eisenberg, Robert Guy, A Proof of the Hairy Ball Theorem, The American Mathematical Monthly, Vol. 86, Non. 7 (Aug. - Sep., 1979), pp. 571–574. (n'inglés)

Enllaces esternos

• Esta obra remanez de la traducción parcial de Théorème de la boule chevelue de Wikipedia - francés, concretamente d'esta versión, espublizada polos sos editores baxo la Llicencia de documentación llibre de GNU y la Llicencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
• Esta obra remanez de la traducción parcial de Hairy ball theorem de Wikipedia - inglés, concretamente d'esta versión, espublizada polos sos editores baxo la Llicencia de documentación llibre de GNU y la Llicencia Creative Commons Atribución-CompartirIgual 3.0 Unported.