Coordenaes horizontales

Coordenaes horizontales
Coordenaes celestes

Les coordenaes horizontales son un sistema de coordenaes celestes referíes al horizonte del observador y a la so vertical.

Pa determinar l'allugamientu d'una estrella en coordenaes horizontales, un observador tien de midir la so altura que ye la distancia angular dende'l horizonte hasta l'estrella. En segundu llugar, tien de determinar l'ángulu que forma l'estrella con una direición que se toma como orixe, xeneralmente'l sur (n'astronomía) o'l norte (navegación) midida sobro l'horizonte y en sen horariu. Tal ángulu nómase azimut.

Les coordenaes horizontales dependen del observador. Ye dicir, que nún mesmu momentu, un astru adícase baxo coordenaes horizontales desemeyaes por observadores distintos, allugaos en puntos diferentes de la Tierra. Esto significa que tales coordenaes son llocales.

Conceutos fundamentales

Figura 1. L'horizonte astronómicu d'un observador sobro la superficie de la Tierra, nel puntu O, ye'l círculu máximu SWNE. Nesta imaxe hai de facer una correición: l'observador alcuéntrase nel planu de dichu horizonte. Sicasi, el tamañu de la Tierra ye tan pequeñu comparáu col universu que, sacante pa oxetos mui cercanos, como la Lluna y los planetes, la correición ye pequeña.

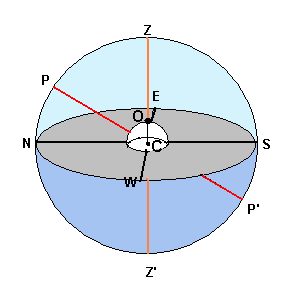
Seya C el centru común de les esferes terrestre y celeste (figura 1). Se conseña un puntu O sobro la superficie terrestre, tal que OC ye la vertical de plomada n'O. L'observador tá n'O.

La prollongación d'OC corta a l'esfera celeste nos puntos Z y Z' , zenit y nadir de O, respeutivamente. La llinia ZZ' ye la vertical del observador, o cenciellamente la vertical.

Por C imaxinamos un planu perpendicular a ZZ' que taya a l'esfera celeste nel círculu máximu SWNE, l'horizonte astronómicu d'O. No sucesivo, cuando falemos d'horizonte, pescanciarase siempre horizonte astronómicu, esceutu avisu contrariu.

La prollongación del exe terrestre danos los puntos P y P' , los polos de la esfera celeste. PP' ye'l exe del movimientu diurnu. La rotación de la Tierra fai que la esfera celesta muévase aparentemente alrodiu d'esi exe.

Les proyeiciones de P y P' nel horizonte son los puntos N (Norte) y S (Sur), y la perpendicular a la llinia NS por C, nel planu del horizonte, danos l'Este E y Oeste W.

Na realidá l'observador ta nel planu del horizonte. Les coordenaes horizontales son topocéntriques. Esto supón que les midíes qu'obtenga sedrán aparentes, pol paralax diurnu y la refraición atmosférica. Según los casos, requeriranse les correiciones afayaíces, pa tresformar estes midíes en coordenaes xeocéntriques.

La vertical del observador ZZ', el so horizonte SWNE y el puntu Sur S, son el sistema de referencia de les coordenaes horizontales.

Más conceutos fundamentales

Figura 2. L'altura y l'azimut d'un astru son les sos coordenaes horizontales: l'altura h de X ye l'ángulu XCX', y el so azimut A l'ángulu SCX'

Imaxinamos agora a la Tierra reducida al puntu C nel centru de laesfera celeste (figura 2)

La vertical ZZ' ye una llinia y determina infinitos planos perpendiculares al del horizonte. Caún d'esos planos taya a l'esfera celeste nos círculos verticales', o cenciellamente los verticales que pasen siempre pel zenit y el nadir. Ye necesaria la matización llingüística: la vertical ye siempre la llinia ZZ', mentanto quel vertical ye ún de los círculos verticales.

De los infinitos verticales sollíñense dos:

• Meridianu: el vertical PZSZ' que caltién a los polos. Taya a l'horizonte nos puntos cardinales Norte -N- y Sur -S-. La parte del meridianu que caltién al cénit, Z, ye'l meridianu superior PZP', y la que caltién al nadir, Z', ye'l meridianu inferior PZ'P'.

• La interseición del Meridianu col planu del horizonte ye la llinia meridiana que taya a l'esfera celeste nos puntos cardinales N y S.
• Primer vertical: el vertical ZEZ'W, perpendicular al meridianu, qu'interseuta col horizonte determinando los puntos Este -E- y Oeste -W-.

• La interseición del Primer vertical col planu de l'horizonte ye la llinia perpendicular que seiciona a la esfera celeste nos puntos cardinales E y W.

Las llinies meridiana y perpendicular formen un sistema de referencia perpendicular qu'apunta a los cuatro puntos cardinales.

La rotación aparente de la esfera celeste d'exe PP fai que los astros aprucen pel este, (en realidá namái risquen pol este si la so declinación ye cero) s'eleven y algamen la so máxima elevación nel meridianu superior (culminación), pa dempués amiyar y ponese pel oeste (ocasu). Siguen el so camín per baxo l'horizonte y nun s'adiquen hasta'l día siguiente nel que risquen otra vegada.(ortu).

L'intervalu de tiempu ente dos culminaciones socesives, o pasos pel meridianu ye'l día sidéreu, 3 minutos y 55,9 segundos más curtiu que'l día solar mediu.

L'azimut y l'altura

Seya X un astru de la esfera celeste, CX la so direición, y CX' la proyeición d'ésta nel planu del horizonte (figura 2). Definimos:

• altura de X (h o a) ye l'ángulu XCX', ye dicir l'ángulu ensamáu pola so direición y l'horizonte. Tamién podemos considerar a l'altura como l'arcu XX'.

L'altura ye positiva sobro'l horizonte, y negativa per debaxo d'él, nesti casu denómase depresión. Asina l'altura del cenit val 90º, y la depresión del nadir ye de -90º.

• Acimut de X (A) ye l'ángulu SCX', ye dicir, l'ángulu formáu por CX' y la direición Sur.

L'acimut, referíu al puntu Sur , ye positivu en sen SWNE, el movimientu aparente del cielu celeste. Un acimut mayor de 180° pue tomase en sen contrariu pero con valir negativu. Por exemplu, el puntu Oeste, W, tien un acimut de 90º, y el puntu Este, E, tienlu o bien de 270º, o bien -90º.

Como s'apuntó na introducción, hai convenios que refieren l'acimut al puntu Norte (pa la navegación, non n'astronomía) N, col sen positivu NESW.

Laltura y lacimut son les coordenaes horizontales de X.

L'altura ye un ángulu o un arcu, y non una distancia llinial. Pa evitar la confusión, davezu denómase elevación.

Distancia cenital

L'ángulu ZCX ye la distancia cenital de X, la so distancia angular al polu, denotada por z. Evidentemente:

z + h = 90º

La distancia angular del polu al horizonte ye la altura del polu, ángulu PCN pal Hemisferiu Norte, y P'CS pa l'Hemisferiu Sur, ye la llatitú del llugar au s'alcuentra l'observador O. Denótase con $\varphi$ -lletra griega phi, lleer fí-.

Toes aquelles estrelles que tienen distancia al polu menor o igual que dicha llatitú nun tán enxamás per baxo l'horizonte, de mou que nun se ponen: son les estrelles circumpolares pa O. Les sos trayeutories son círculos concéntricos a los polos. Como casos estremos comparemos lo qu'asocede nel Ecuador terrestre y nos polos:

• Nel Ecuador, au $\varphi$= 0º, nenguna estrella sobro l'horizonte ye circumpolar, y ñacen y pónense perpendicularmente al horizonte. El polu tá nel finxu la tierra.

• Nos polos, au $\varphi$= 90º ó -90º, toles estrelles sobro l'horizonte son circumpolares, nun ñacen nin s'oculten. El polu ta nel cenit.

L'ángulu complementariu de la llatitú ye la collatitú o distancia cenital del polu. Darase la siguiente rellación:

$\varphi$ + collatitú = 90º

Midición d'altures

Paralax diurnu

Figura 3. Les paralaxes horizontal y diurna o d'altura vienen determinaes porque l'observador s'alcuentra nel horizonte aparente y non nel horizonte astronómicu. Asina, a él paez-y que B' tá más altu que B, cuando na realidá tán a la mesma altura, darréu que comparten la direición xeocéntrica CT.

L'altura h d'un astru, ha de medise respeutu a l'horizonte astronómicu del qu'allupa, pero ésti tómala dende'l so horizonte aparente, nel puntu O, y lo que realmente obtien ye l'altura aparente del astru. Surde el fenómeno de paralax (Figura 3)

Dende O l'astro B vese en N, metantu que dende C veríase en T, más altu que N. L'estrella camuda de posición según la direición del observador. Esto ye, el paralax diurnu o d'altura.

Paralax diurnu ye l'ángulu formáu poles direiciones topocéntrica y xeocéntrica d'un astru. Na figura 3, y pa B:

• Direición topocéntrica ON: direición dende'l llugar que s'ocupa.
• Direición xeocéntrica CT: direición dende'l centru de la Tierra.

Cuando l'astru s'alcuentra nel horizonte aparente del observador, resulta la paralax horizontal. Tal ye'l casu del oxetu A que tien por paralax horizontal l'ángulu LAM =CAO

El paralax diurnu amenorga cola elevación sobro l'horizonte, y cola distancia del oxetu adicáu:

• Cola elevación: comparamos B con A. La paralax NBT de B ye menor que la paralax LAM d'A. A mayor elevación menor paralax. Nel cenit la paralax es nula.

• Cola distancia del oxetu observáu: comparamos B y B'. Dambos tienen la mesma elevación (neta direición xeocéntrica), pero tán a distintes distancies de la Tierra. La paralax SB'T de B' (más llonxanu) ye nidiamente menor que la paralax NBT de B (el más cercanu). A mayor distancia menor paralax.

Les distancies nel espaciu son descomanadamente grandes, y por eso les paralaxes diurnes son despreciables na mayoría de los casos. En distancies mui pequeñes como les del Sistema Solar, son de consideración, pero namái. La Lluna tiene un paralax que supera el grau -61' 50"-, cantidá enforma importante que nun se puede desdexar. Pal Sol ye d'unos 9" malapenes. Pero pa Próxima Centauri a namái 4,2 años lluz la paralax ye del orde de la cienmilésima de segundu, y eso siendo l'estrella más próxima a nosotros. La paralax diurna d'una estrella ye práuticamente nula.

La paralax denótase con $\pi$ -lletra griega pi. Lleer pí-

Pa un paralax significativu tenemos:

h_real = h_aparente + $\pi$

La refraición

Figura 4. La refraición fai que l'altura aparente d'un astru seya superior a l'altura real. D'esta miente el Sol baxo l'horizonte, en S, vese en S', sobro'l horizonte

No que respeuta a la refracción atmosférica la cosa ye distinta porque si bien amenorga cola altura lo mesmo que'l paralax, per otru llau nun se reduz el so efeutu pola distancia del oxetu adicáu, por grande que seya ésti. La refraición hai de tenela siempre en cuenta al facer midiciones que necesiten precisión.

La figura 4 amuesa un casu típicu de refraición. Cuando'l limbu inferior del Sol (*) cinca l'horizonte del mar, yá nun tá ellí. Lo qu'allupamos ye la so imasen refractao en S', y l'estrella yá tá dafechu per baxo'l finxu del horizonte, en S.

L'efeutu de la refraición R sobro l'altura d'un astru ye opuestu al efeutu que producía la paralax: ésta fai que l'altura aparente seya menor que la real, la refraición fai que l'altura aparente seya mayor que la real, eleva al astru, de mou que darase la rellación:

h_real = h_aparente - R

La refraición ye máxima nel horizonte, y nula nel cenit, al igual que la paralax. A una altura de 0º val 33' 48". A 10º d'altura yá s'amenorga a 5' 13". Ente los 40º y 50º val 1', y a partir de los 80º tá per debaxo de los 10".

---

(*) _{El limbu inferior del Sol ye'l so berbesu inferior vistu dende la Tierra}

---

Ver tamién

• Coordenaes ecuatoriales
• Paralax
• Paralax diurnu

Enllaces esternos

• Wikimedia Commons tien conteníu multimedia tocante a Coordenaes horizontales.

• Datos: Q625696
• Multimedia: Horizontal coordinate system